| 投擲硬幣次數 | 硬幣正面朝上次數 | 正面朝上的次數比例 |
|---|---|---|
| 1 | 0 | 0.00 |
| 2 | 1 | 0.50 |
| 3 | 2 | 0.67 |
| 4 | 3 | 0.75 |
| 5 | 4 | 0.80 |
| 6 | 4 | 0.67 |
| 7 | 4 | 0.57 |
| 8 | 5 | 0.63 |
| 9 | 6 | 0.67 |
| 10 | 7 | 0.70 |
| 11 | 8 | 0.73 |
| 12 | 8 | 0.67 |
| 13 | 9 | 0.69 |
| 14 | 10 | 0.71 |
| 15 | 10 | 0.67 |
| 16 | 10 | 0.63 |
| 17 | 10 | 0.59 |
| 18 | 10 | 0.56 |
| 19 | 10 | 0.53 |
| 20 | 11 | 0.55 |
7 機率入門
(上帝)只允許我們置身於…機率的微光之中。
– 約翰·洛克
到目前為止,本書已介紹過一些實驗設計的關鍵原則,並且稍微介紹如何製作一個資料集總結報告。對於許多人來說,統計學就是這些工作的總和:收集所有數字,計算平均值,繪製統計圖,再將這些素材整理在一份報告中裡。這些工作有點像是做數字的拼貼畫,然而,統計學的作用遠多於這些工作。事實上,描述統計學只是統計學最小的一部分,也是功能最不強大的一部分。統計學更有用的一部分是提供以資料進行推論的訊息。
一旦你能從推論的角度來看待統計學,認為統計學是幫助我們從資料中歸納出結論,就會在許多資訊媒介上看到各式各樣能用統計學處理的例子。例如,以下是來自《雪梨晨鋒報》(2010年10月30日)的簡短報導摘錄:
“我現在的工作很艱困,”面對一項表明她的政府現在是歷史上最不受歡迎的工黨政府的民調結果,總理如是說。預估初選執政黨能獲得23%的選票。
這種報導在報紙或日常生活中並不特別吸引人,但讓我們思考裡面所提示的資訊。民調機構做的民意調查,通常是相當大規模的,因為這些機構有資金。由於原作者太懶了,不想查找原始資訊,所以讓我們假裝這家機構隨機調查了1000位住在新南威爾斯(NSW)的選民,其中230人(23%)聲稱他們打算投票給澳大利亞工黨(ALP)。根據澳大利亞選舉委員會的報告,2010年聯邦大選登記在新南威爾斯投票的選民有4,610,795位,所以其餘4,609,795名選民(約99.98%的選民)的意見對我們來說是一片混沌。即使就當沒有人在民調中說謊,我們可以100%確定的是,ALP真正的初選得票數就是在230/4610795(約0.005%)和4610025/4610795(約99.83%)之間。那麼看了民調結果的民調機構、報社和讀者得出ALP的初選得票大約只有23%的結論是依據什麼?
這個問題的答案很明顯。如果我隨機打電話給1000人,其中230人表示打算投ALP,這些人很可能並不是全體選民裡真正要投給ALP的唯一230人。換句話說,我們假設民調機構收集的資料能代表所有有投票權的選民。但是究竟有多少代表性呢?如果開票後,ALP得到的初選票實際上是24%? 甚至是29%或 37%? 這時候只憑直覺的想法會開始有點動搖。沒有人會對24%感到驚訝,但是會對37%感到驚訝,然而很難說29%會讓人相信民調結果。在這個狀況,我們需要比查看數字和直覺猜測更強大的工具。
推論統計學提供我們回答這些問題所需要的工具,而且這類問題就是科學研究工作的核心,每門簡介統計學和研究方法課程的一大部分單元都是在學推論統計。然而,推論統計的理論基礎是建立在機率論,因此這個單元要討論機率論,內容是了解機率論必須掌握的背景知識。本單元沒有太多統計學,讀者也不用像其他單元一樣,需要深入理解這個單元的所有內容。儘管如此,由於機率論是推論統計的重要基礎,認識一些基本的機率論知識是值得的。
7.1 機率和統計有什麼不一樣?
開始談論機率論之前,先花點時間思考機率與統計學之間的關係是很有幫助的。這兩門學科關係密切,但是兩者是不一樣的。機率論是“隨機事件的理論”,是數學的一個分支,用來探討不同種類的事件發生的次數/頻率。例如,使用機率論可以回答以下這些問題:
連續投擲一枚公平的硬幣,投出10次正面的機率是多少?
如果投擲6面骰子兩次,兩次都是6點的可能性有多大?
從經過完整洗牌的一組撲克牌,抽出5張紅心的牌可能性有多大?
我買的這一期彩劵中獎的機率是多少?
這些問題都有一些共同點。在所有可預料會發生的結果,“事實宇宙”是可知的,問題的答案與“什麼樣的事件”會發生有關。 第一個問題,我知道硬幣是公平的,所以每次硬幣正面朝上都有50%的機率。第二個問題,我知道一枚骰子擲到6的機率為1/6。第三個問題,我知道洗牌後的撲克牌,抽到那一張的機率都是1/52。第四個問題,我知道彩劵中獎遵循發行商訂下的規則。共同關鍵是每個機率問題都是來自已知的世界模型,使用模型做點計算,我們就可以知道答案。
機率模型可以非常簡單。以擲硬幣的問題來說,模型可以寫成這樣:
\[P(\text{正面})=0.5\]
我們可以用白話講“擲出正面的機率是0.5”。 正如稍後會看到的,就像表達百分比只有用0%到100%之間的任何一個數字,機率只用從0到1之間的任何數字。 使用這個機率模型回答第一個問題時,其實我並不知道會發生什麼事。也許會像問題所問的,我真的會擲出10次正面,但也許我會擲出3次正面。這就是關鍵所在:在機率論的世界,模型是已知的,但是資料是未知的。
那麼統計學呢?統計學解決問題的原則剛好相反。在統計學世界裡,我們並不知道世界的真實樣貌。唯一能掌握的只有資料,我們想要從資料中獲得世界的真實樣貌。用統計學問同樣的四道問題,會像是這樣:
如果我朋友當面擲了10次硬幣全是正面,他是不是在耍老千?
如果賭場莊家用一顆6面骰子,連續丟兩次都是6點,這顆骰子有機關的可能性有多大?
如果一組撲克牌最前面的五張牌都是紅心,這副牌洗牌不夠徹底的可能性有多大?
如果是彩劵行的老闆娘中了頭獎,這期開獎有人作假的可能性有多大?
在這裡我們唯一擁有的就只有資料。我能知道的是,我看到我的朋友擲硬幣10次,每次都是正面。我能做推論的是我應不應該相信眼前看到的是使用公平硬幣而出現的結果,還是應該懷疑我的朋友在耍我。這個場景我得到的資料如下:
正面 正面 正面 正面 正面 正面 正面 正面 正面 正面
我要努力弄清楚我應該相信哪種“世界模型”。 如果硬幣是公平的,那麼我應該相信的模型是正面機率為0.5,即 \(P(\text{正面}) = 0.5\)。 如果硬幣是有機關的,那麼我應該判斷出現正面的機率不是0.5,可以寫成 \(P(\text{正面})\neq0.5\)。 換句話說,使用推論統計的目標是要弄清楚那一種機率模型是正確的。統計問題與機率問題顯然不是一樣的,但是兩者之間有深刻的關聯。因此,要充分學懂統計理論,就要從認識什麼是機率及運算機率的定理開始。
7.2 如何解讀機率?
讓我們先談談如何回答第一個問題:什麼是“機率”?統計學家和大多數的數學家同意機率的運算規則是,但是很少人知道兩方對於如何解釋這個問題沒有太多共識。這似乎很奇怪,因為很多人都非常習慣使用 “可能性”(chance)、“很有可能”(likely)、“有可能”(possibe) 和 “很可能”(probable) 這類詞彙,回答這個問題似乎不應該很困難。但是,你我都可能有過這樣經驗,聽不懂兩方人馬的對話究竟在講什麼,你我一樣的平凡人會默默走開,而且之後完全記不得兩方的對話。
讓我用這個例子來試著解釋什麼是機率。假如有一場機器人足球賽,上場的球隊是阿杜伊諾阿森納和米蘭,我想賭其中一隊會贏球。經過深思熟慮後,我判斷阿杜伊諾阿森納隊勝出的機率為80%。我這麼說是什麼意思呢?其中有三種可能意義:
雙方是機器人球隊,他們可以比賽無數次,如此一來,以所有比賽結果平均來說,阿杜伊諾阿森納會贏得每10場比賽中的8場。
看一看任何一場比賽的下注賠率,我花1美元押米蘭隊贏球,他們贏我就能獲得5美元(拿回我押的1美元再加上4美元的贏球獎勵)。相對地,我花4美元押阿杜伊諾阿森納隊贏球,他們贏我也能獲得5美元(拿回我押的4美元再加上1美元的贏球獎勵)。
我對阿杜伊諾阿森納隊獲勝的主觀“信念”或“信心”,比米蘭隊獲勝的信念高出四倍。
這些解釋似乎都有道理。然而,每種解釋的意義是不一樣的,並且不是每位統計學家都會認同所有解釋。原因是現代統計學存在壁壘分明的門派(沒錯,真的有!),並且會因為你追隨其中一派學習久了,你會認為另一派的解釋毫無意義。在這一節,我簡單介紹文兩大主要門派的方法論。不過請讀者記得,這兩種主要方法論,沒有那一方是統計學的唯一方法論。
7.2.1 次數主義觀點
兩大觀點中佔現代統計學主導地位的是次數主義觀點(frequentist view)1,這個觀點將機率定義為長期累積次數。假如我們投擲一枚公平硬幣無數次,按照次數主義的定義,這一枚硬幣的機率模型是\(P(H)= 0.5\)。那麼可能的觀察結果是什麼?某次連續投擲20次的結果可能像以下紀錄:
反,正,正,正,正,反,反,正,正,正,正,反,正,正,反,反,反,反,反,正
在這20次裡有11次為正面(55%)。 假如一直記錄下去,以\(N_H\)表示擲出正面的次數,\(N\)代表累積至紀錄當下的總次數,每次紀錄計算擲出正面的比例就是 \(\frac{N_H}{N}\)。 表 7.1 整理我得到的結果(原作者的親自實驗結果!):
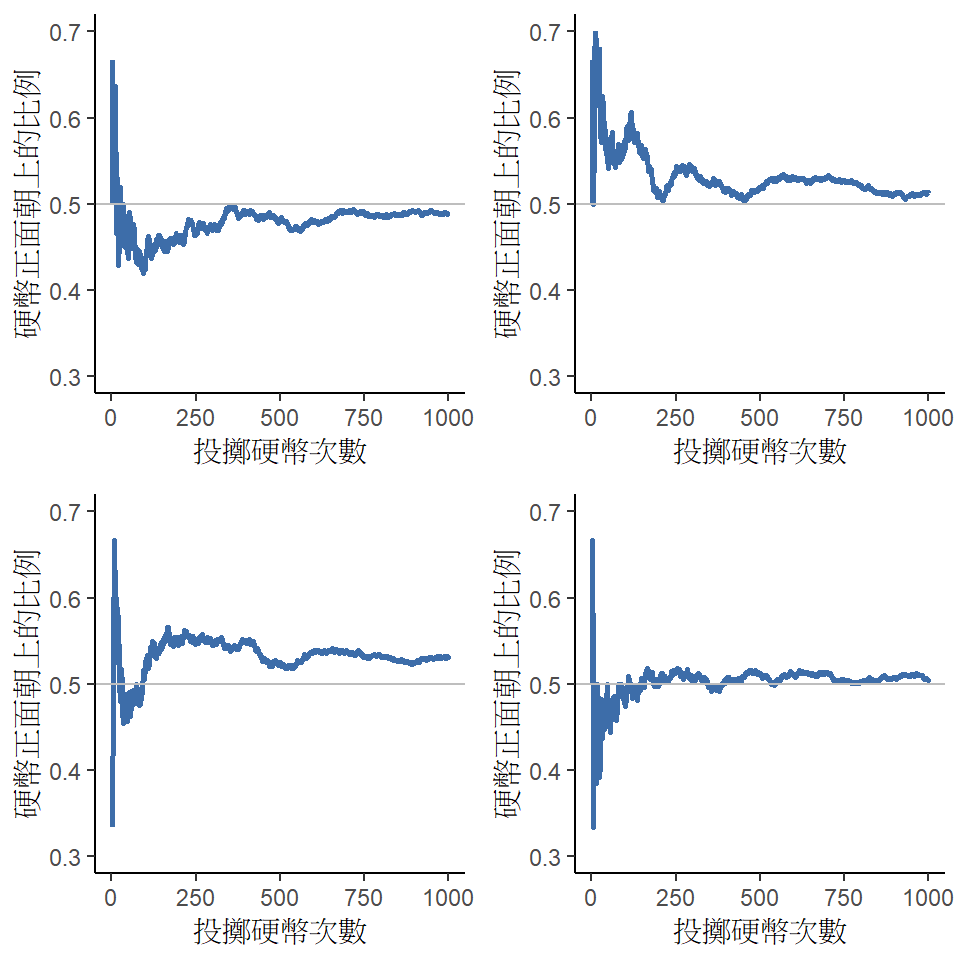
留意一下這次實驗一開始,擲出正面的比例波動很大,一開始是\(.00\),後來陡升至\(.80\)。到後來,累積的紀錄越来越多,比例值會接近多數人印象中的“正确”答案 \(.50\)。這就是次數主義觀點對於「機率」的核心定義:一次又一次地擲出一枚公平的硬幣,當 N 越大(接近無窮大,數學表示為 \(N \rightarrow \infty\) ),正面的比例將收斂至 50%。數學家還會關注一些其他技術細節,但是以質性的角度來說,這就是次數主義論者定義機率的方式。可惜的是,我没有辦法拿到無限數量的硬幣,還有反覆做無限次地投擲硬幣所需要的耐心。不過只要有一台電腦,就可以讓電腦做不必動腦的重複性作業。所以我用電腦模擬投擲硬幣1000次,然後畫出隨著\(N\)增加, \(\frac{N_H}{N}\) 的比例如何變化的趨勢圖。為了確保這不是偶然發生的現象,我做了四次獨立的模擬計算。模擬結果就像 圖 7.1 。如圖所示,擲出正面的比例值最後會停止波動並趨向中間的數值,趨勢線最後停留的數值就是擲出正面的真實機率值。
次數主義觀點的機率定義有一些理想化的條件。首先,觀察必須是客觀的。事件發生的機率必然取決於事實,機率模型的數學表述式,只有定義其中的符號代指物理世界所發生的一系列事件才有意義。2 還有,每個機率事件是可被明確觀察的。任何兩個人觀察同一種事件的所紀錄的發生序列,都能用來計算特定事件的機率,計算的結果必定會相同。
然而次數主義方法論要成立的條件很難達成。首先,物理世界並不存在無窮序列。就拿你錢包裡的硬幣來說,拿出來做擲硬幣實驗,每次落地都會撞到地面,每撞擊一次都會磨損硬幣表面一點,最终這枚硬幣會被磨光。有些同學聽了可能會問,討論能“無限次”擲硬幣的假設是有意義的概念,還是客觀的概念,對於了解機率是什麼有何幫助?物理世界不會存在任何無限的事物,所以“無限序列”的機率事件不可能是真實的。更嚴重的是,次數主義定義容許的範圍非常狹窄。人類的語言能力可以給很多看得到的事物發生用機率表達,但是就理論來說,也無法將機率對應到假想的事件序列。例如,如果澳洲電視台的氣象預報員說“2018年11月2日阿德雷德降雨的機率是60%”,所有人都很樂意接受這種說法,但是很難用次數主義的條件來定義報導中所提的機率。 全世界只有一個地方叫阿德雷德,2018年11月2日也只是一個時間點。所以不存在無限序列,只是一時一地的單一事件。然而,次數主義的機率觀點不允許我們對單一事件以機率描述。從次數主義的角度來想,明天要麼下雨,要麼不下雨,不可重複事件不可能有“機率”。 其實次數主義的追隨者可以使用一些非常聰明的技巧來解決這道難題,一種方案就像有的氣象預報員會用的說辭:「以我所使用的預測方法,只要出現某些氣象條件就能預測60%的降雨機率。只要明日的氣象具備這些條件,預測有60%的降雨機率是合理的。」這樣的說法好像繞了好幾圈又違反直覺,不過之後的單元裡,我們會看到這套次數主義方法論如何形塑現代統計方法(例如 小單元 8.5)。
7.2.2 貝氏觀點
貝氏的機率觀通常也稱為主觀觀點,雖然這個觀點在統計學領域中一直是少數派,但是影響力在過去幾十年持續穩定增長。 貝氏一門還有很多分支,以至於難用三言兩語說明什麼是“貝氏”觀點。解釋主觀機率的最常見說法是將事件的機率定義為有智慧與理性能力的現代人對於事件發生的信念程度(degree of belief)。從這個角度進一步說,機率並不存在於現實世界,而是存在於人類及其他智能生物的思維和想像。3
然而,為了實際應用主觀機率發展出來的方法,我們需要先把“信念程度”轉換為可操作的形式。今天已經發展出許多方法,在此介紹的形式化方法是“理性博弈”(rational gamling): 假如我相信明天下雨的機率為 60%。若有人讓我下注,賭明天下雨的話,我會贏5美元,如果沒下雨,我就輸5美元。從我的角度來看,這顯然是一個相當不錯的賭注。 換句話說,如果我看到明天降雨機率只有 40%, 那麼接受這個賭注就是不明智的。 因此,我們可以通過我願意接受的賭注大小操作“主觀機率”。
貝氏的方法論有什麼優缺點? 主要優點是你能指定想要評估的任何事件是否發生的機率,而且不必考慮那些事件會不會重複。對許多人來說,最大的缺點是你不能完全客觀看待機率事件。指定一個事件機率需要一個對應信念程度的實體,這個實體可能是一個人類、外星人、機器人或者甚至一個統計學家,無論如何必須設定存在一位持有某種信念的智能代理者。對許多計較客觀的學者來說,這是令人不舒服的想法,似乎會讓機率運算變得武斷。儘管貝氏方法論強調信念的代理者是理性的(遵守機率規則),但是每個人都可以有屬於自己,不一定和他人相同的信念。以前面的擲硬幣問題來說,觀察者A可以相信硬幣是公平的,而觀察者B不需要,不過兩者的看法都是理性的。次數主義觀點則不允許任兩位觀察者認為同一事件的機率有不同看法。如果有這種情況,至少其中一種看法是錯的。 然而貝氏方法論觀點容許歧異看法並存的情形, 不同背景知識的兩造觀察者,(在貝氏的機率擂台)可以合法地對同一事件持有不同信念。簡而言之,次數主義觀點有時被認為範圍太狹窄(禁止觀察者對許多事件指定機率),貝氏觀點有時則被認為範圍太廣泛(允許觀察者保留彼此看法的差異)。
7.2.3 觀點之間的差異是什麼?何者正確?
既然你已經看懂了這兩種觀點的核心想法,比較兩方觀點的差異有助你回答什麼是機率。回頭來談那場機器人足球比賽結果的三種解釋,你認為次數主義和貝氏兩種觀點會如何看待那種是最正確的機率定義?次數主義的追隨者會說那個解釋最符合他們心目中的機率觀?貝氏的追隨者會贊成那一個?那個解釋對於兩方來說毫無意義?如果您有充分理解兩派觀點,應該多少能回答以上的問題。
好啦,假如你真的理解觀點之間的區別,你應該想知道那一種觀點是正確的?老實說,我不知道有沒有正確的答案。據我所知,次數主義追隨者思考事件序列的方式,以數學來看沒有什麼不正確的,貝氏觀點設定一個持有信念的理性代理者,這一點也有數學基礎。其實,如果讀者能研究得更深入,會發現兩個觀點在很多事情的意見是一致的。許多基於次數主義方法所做出的決定,也是貝氏觀點追隨者認為一個理性代理者也有相同結論;許多貝氏主義方法具有相當明顯的次數主義特性。
我(原作者)自認是務實主義者,所以我會使用任何可相信的統計方法。工作多年的經驗,使我更喜歡貝氏方法,理由我將在本書的最後單元解釋。但是我並不會不再使用次數主義方法,而且不是每個人都能在兩種觀點之間自在轉換。像是 羅納德·費雪爵士(Sir Ronald Fisher),20世紀統計學巨擘之一,就是徹底反對貝氏觀點,立場最極端的反對者。他在討論統計學數學基礎的著作裡提到主觀機率觀點是 “不可突破的叢林,(放任發展)會阻止精確統計學概念的進步” (Fisher, 1922, 第 311 頁)。反方代表如心理學家保羅·米爾(Paul Meehl),他認為依靠次數主義方法會讓科學家變成 “能生產知識但無法提出真正洞見的書呆子,,與次數主義相伴的快樂學術路上留下了一整列受害者,其中沒有任何人輸出的科學知識能有效地開枝散葉”(Meehl, 1967, 第 114 頁)。讀者有心挖掘爭論觀點的文獻會發現,現代統計學的歷史和暢銷小說一樣精采。
無論如何,雖然我(原作者)比較喜歡貝氏主義的觀點,但大多數統計分析都是建立在次數主義方法論,有用的推論方法都有實用價值。本書介紹的統計方法與多數心理學系統計課內容大致相同,如果讀者想了解大多數心理學家使用的統計工具,需要好好掌握次數主義方法。我能保證,學習次數主義的統計方法不會浪費時間。就算之後有一天想要跳到貝氏的陣營,讀者也應該至少要讀通一本談論 “正統” 次數主義觀點的書。此外,我不會完全忽略貝氏觀點。之後每個章節,我會在適當的段落添加一些貝氏觀點, 最後的 單元 16 會詳細介紹貝氏觀點的統計方法。
7.3 基本機率論
7.3.1 機率分佈入門
我(原作者)個人最難以啟齒的一件事情是,我的衣櫃裡只有5條褲子。三條牛仔褲,一件西裝褲和一條運動褲。更讓我的朋友感到無聊的是,每條褲子都有個代號:\(X_1\)、\(X_2\)、\(X_3\)、\(X_4\) 和 \(X_5\)。這是真的,這是為什麼我的朋友都叫我「內心小劇場男子」。每個要外出的日子,我都會想好要穿那一條。即使我充滿想像力,也不會想要穿兩條褲子出門,而且都活了這麼久,我不會不穿褲子就出門。如果要用機率論的語言來描述我今天穿那條褲子出門,每條褲子的代號( \(X\) )合稱為基本事件。基本事件的關鍵條件是每紀錄一次觀察,紀錄結果可用其中一個代號代表,像是每天我穿了其中一條褲子就紀下這條的代號。因為現在我出門只會穿一條褲子,每一天穿那條褲子出門的紀錄剛好滿足基本事件的條件。同樣的,所有可能發生的基本事件集合稱為樣本空間。當然,我的朋友或有些學生會說“衣櫃”,那是因為他們不想用機率的詞彙來想像我的褲子。哭哭。
好的,現在有一個樣本空間(衣櫃),包括許多可能的基本事件(今天穿出門的褲子),現在要做的就是為每一個基本事件分派一個機率。對於其中一個事件\(X\),該事件的機率\(P(X)\)是介於0和1之間的數字。\(P(X)\)的值越大,事件發生的可能性就越大。例如\(P(X)=0\) 表示事件\(X\)是不可能發生的(我從不穿那一條褲子出門)。另一方面,\(P(X)=1\) 表示事件\(X\)必定會發生(我總是穿那一條褲子出門)。至於介於兩者之間的機率值,代表我有時候會穿那條褲子。例如 \(P(X)=0.5\)代表我會出門的某幾天,有一半都會穿這條褲子。
到這裡,我們快要建好一套機率分佈模型了。最後一件要知道的事懂是“某個事件總是會發生”。每一天我穿上褲子,我一定會穿好穿滿(你會想這是廢話對吧?)。這幾句陳腔濫調在機率的語彙裡,代表所有基本事件的機率加起來必定等於1。儘管多數人都不太在意,數學家給這個事實命名為總機率律(law of total probability)。更重要的是,只要符合總機率律的條件,就自然會得到了一個機率分佈(probability distribution)。表 7.2 就是有關原作者本人會穿那條褲子出門的機率分佈。
| 褲子樣式 | 事件代號 | 事件機率 |
|---|---|---|
| 藍色牛仔褲 | X_1 | P(X_1)=.5 |
| 灰色牛仔褲 | X_2 | P(X_2) = .3 |
| 黑色牛仔褲 | X_3 | P(X_3) = .1 |
| 黑色西裝褲 | X_4 | P(X_4) = .0 |
| 藍色運動褲 | X_5 | P(X_5) = .1 |
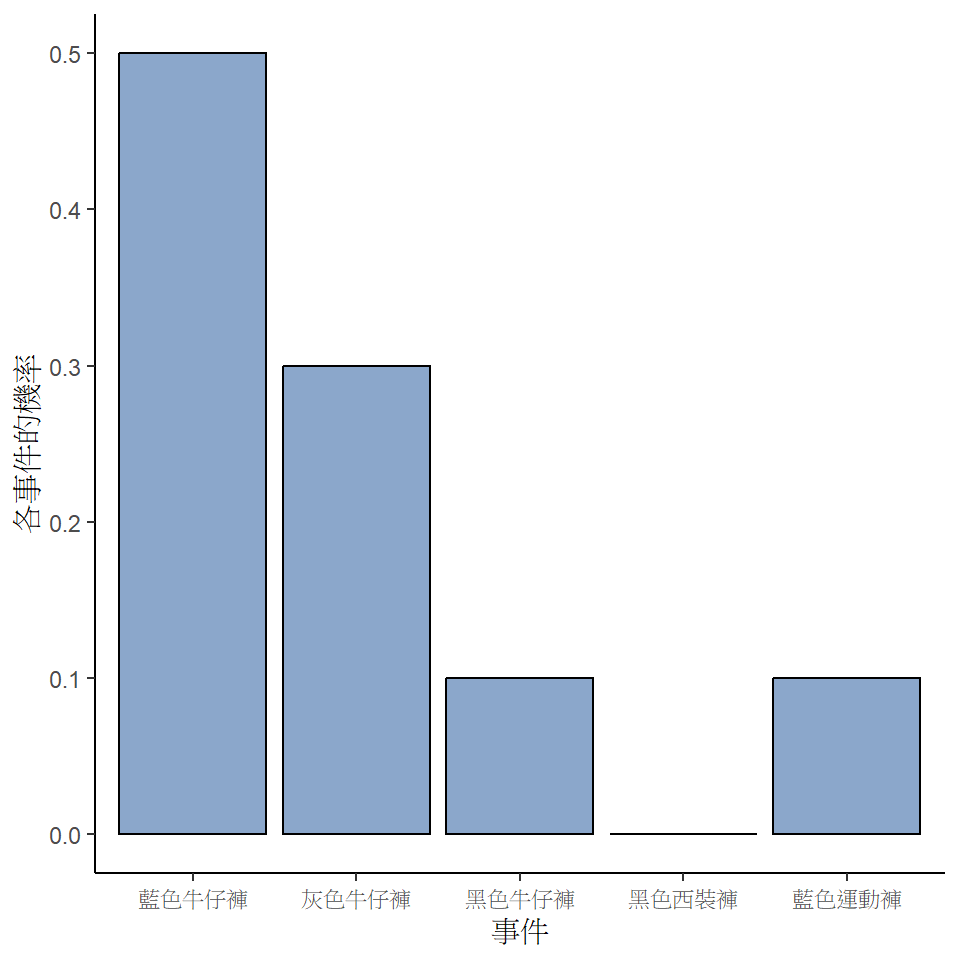
每個基本事件都有一個介於 0 和 1 之間的機率值,只要加總所有事件的機率,會發現總和為 1。太棒了!我們還可以畫出一張漂亮的長條圖將這套機率分佈視覺化(複習一下 小單元 5.3),成果就像 圖 7.2 。到這裡的學習如果沒有意外,代表讀者已經熟悉之後的單元討論機率分佈的方式了,我(原作者)也能用一張圖解釋為何我總是穿牛仔褲出門了! 還需要強調的事情是,機率論容許非基本事件以及基本事件並存。舉個例子來說明,同樣也是用原作者會穿那條褲子出門的機率分佈,要如何用樣本空間裡的基本事件,描述穿任何一條牛仔褲出門的機率?也就是今天出門穿的是“藍色牛仔褲”、“黑色牛仔褲”或“灰色牛仔褲”,都是符合這個狀況的事件。以數學的詞彙來說,我們可以將事件 \(E\) 定義為對應符合條件的基本事件集合 \((X_1,X_2,X_3)\)。只要其中任何一個基本事件發生,就是代表事件 \(E\) 發生。\(E\) 的定義確立後, \(P(E)\) 的機率是多少很容易了,就是全部加起來:因為藍色、灰色和黑色牛仔褲的機率分別是 \(.5\)、\(.3\) 和 \(.1\) ,所以我穿牛仔褲出門的機率等於 \(.9\)。用數學式子表達的話,就是 \[P(E)=P(X_1)+P(X_2)+P(X_3)\]
也許您會認為,這些都太好懂,計算也沒什麼困難,這樣的感覺很多學生都會有。 現在討論的內容只是將日常生活的直觀用一些基本數學算則包裝而已。 不過,從簡單的案例開始,我們能構建一些非常強大的數學工具。 雖然這本書不會討論更深的細節, 表 7.3 列出滿足總機率律的樣本空間,可用的其他運算規則。 這些規則可以從前面描述的基本條件推導,由於本書不會用到這些規則,所以不會展示如何推導。
| English | Notation | Formula |
|---|---|---|
| not A | \(P (\neg A) \) | \(1-P(A) \) |
| A or B | \(P(A \cup B) \) | \(P(A) + P(B) - P(A \cap B) \) |
| A and B | \(P(A \cap B) \) | \(P(A|B) P(B) \) |
7.4 二項分佈
可想而知現在用於統計分析的機率分佈非常多,還有很 多分佈是只有純數學家才會研究的,不過不是所有機率分佈都必須要認識。本書介紹的統計方法主要依靠五種機率分佈運作:二項分佈(binomial distribution)、常態分佈(normal distribution)、 t 分佈(t distribution)、卡方分佈( \(\chi^2\) distribution )以及 F 分佈( F distribution )。所以這個單元後半部就是簡要介紹這五種機率分佈,二項分佈和常態分佈的篇幅會比較多。我們先從二項分佈開始,因為這是五種之中最簡單的機率分佈。
7.4.1 二項分佈入門
機率論的源起是分析博奕遊戲的過程,所以擲骰子或擲幣的實驗經常用做認識二項分佈的教材。現在想像一個簡單的“實驗”:你面前的莊家手裡拿著20個相同的六面骰子,每個骰子的其中一面是骷髏圖案,其他五面都是空白的。如果莊家接著擲出所有骰子,你會看到其中4個骰子的骷髏圖案那面朝上的機率是多少?假如骰子是公平的,我們能假定任何一個骰子擲出骷髏的機率是 1/6。也就是說,擲出一個骷髏機率約為.167。 這些資訊足以回答請你想像的問題,讓我們用機率分佈計算看看。
如同說明本人會穿什麼褲子出門的機率分佈一樣,這裡先要介紹一些名詞和符號。在這個例子裡,我們用\(N\)表示骰子擲出次數,通常被稱為二項分佈的大小參數(size parameter?);還有用\(\theta\)代表一個骰子擲出骷髏的機率,這個參數通常稱為二項式的成功機率4。
我們將使用\(N\)表示我們實驗中的骰子擲出次數,這通常被稱為我們二項分佈的大小參數。 我們也將使用\(\theta\)引用單個骰子出現骷髏的機率,這個量通常被稱為二項式的成功機率5。 最後一個參數 \(X\) 代表這次實驗擲出的幾個骷髏朝上的骰子。因為\(X\)的數值多少是由機率決定的,有個通用名稱隨機變數。有了這些專有名詞和符號,現在能準確地陳述要計算的問題。 我們已經知道 \(\theta = .167\) 還有 \(N = 20\),要計算 \(X = 4\) 的機率。只要知道要用什麼機率分佈計算,任何事件發生機率的通用“數學式”一律可以寫為
\[P(X|\theta,N)\]
表示我們要算出的是 \(X = 4, \theta = .167\) 和 \(N = 20\) 的機率值。
[附加技術細節 6]
我知道很多讀者走到這裡會想:怎麼又是一堆符號,能不用知道那麼多嗎?這本書是為不想學太多數學符號的讀者而設計的,所以接下來會直接談如何運用二項分佈計算機率。不過有些比較好學的讀者可能想知道細節,所以我將詳細公式說明寫在腳注7。因為多數讀者沒興趣知道如何用公式計算機率,本書也不要求讀者要了解公式才能學如何計算,只要看看符合實驗條件 的二項分佈長什麼樣子。
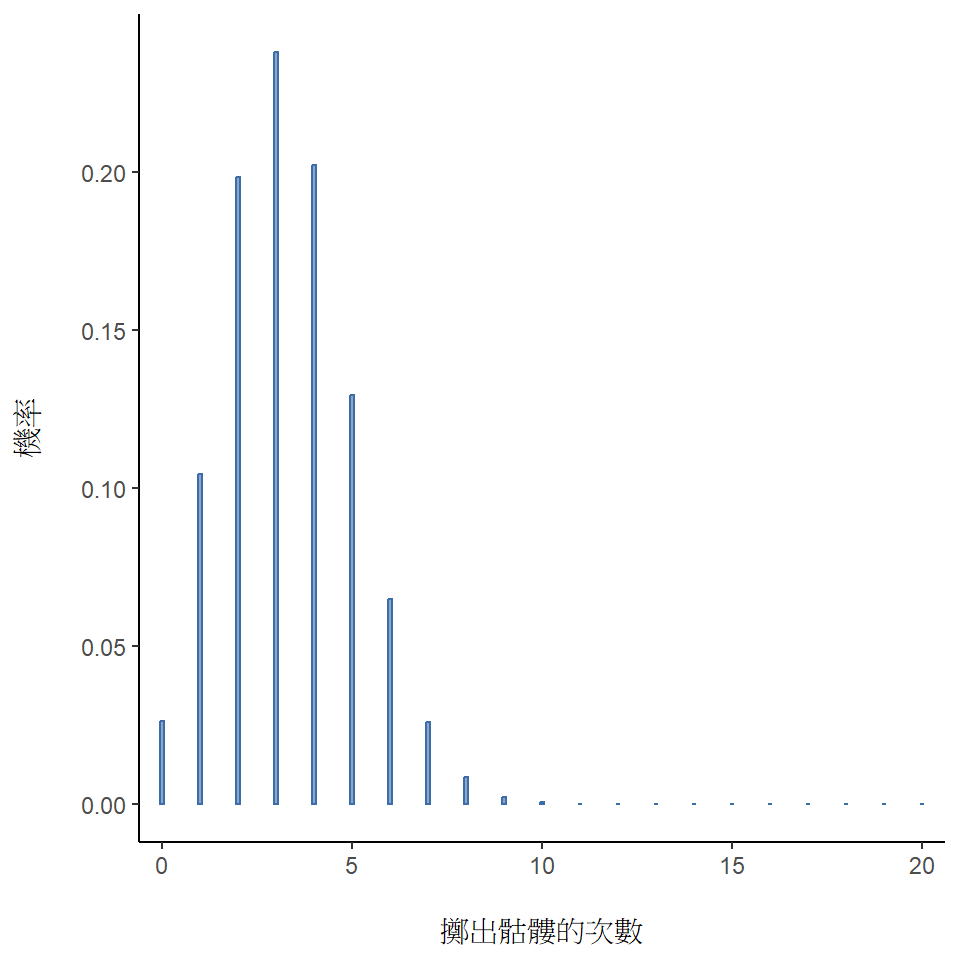
請看 圖 7.3 。這個柱狀圖展示這個擲骰實驗所有可能結果 \(X\) 的出現機率,包括\(X = 0\)(没有一個骷髏) 到\(X = 20\)(全部都是骷髏)。讀者只要知道,解讀這個柱狀圖的方式與 圖 7.2 一樣,水平軸的值代表所有可能的實驗結果,垂直軸的值代表看到各種實驗結果的機率。所以,擲出 \(4\) 個骷髏的機率是約 \(0.20\)(實際答案是 \(0.2022036\),我們很快會學到怎麼算)。也就是說,若你試著重做這個時驗,看到相同結果的機率大約是20%。
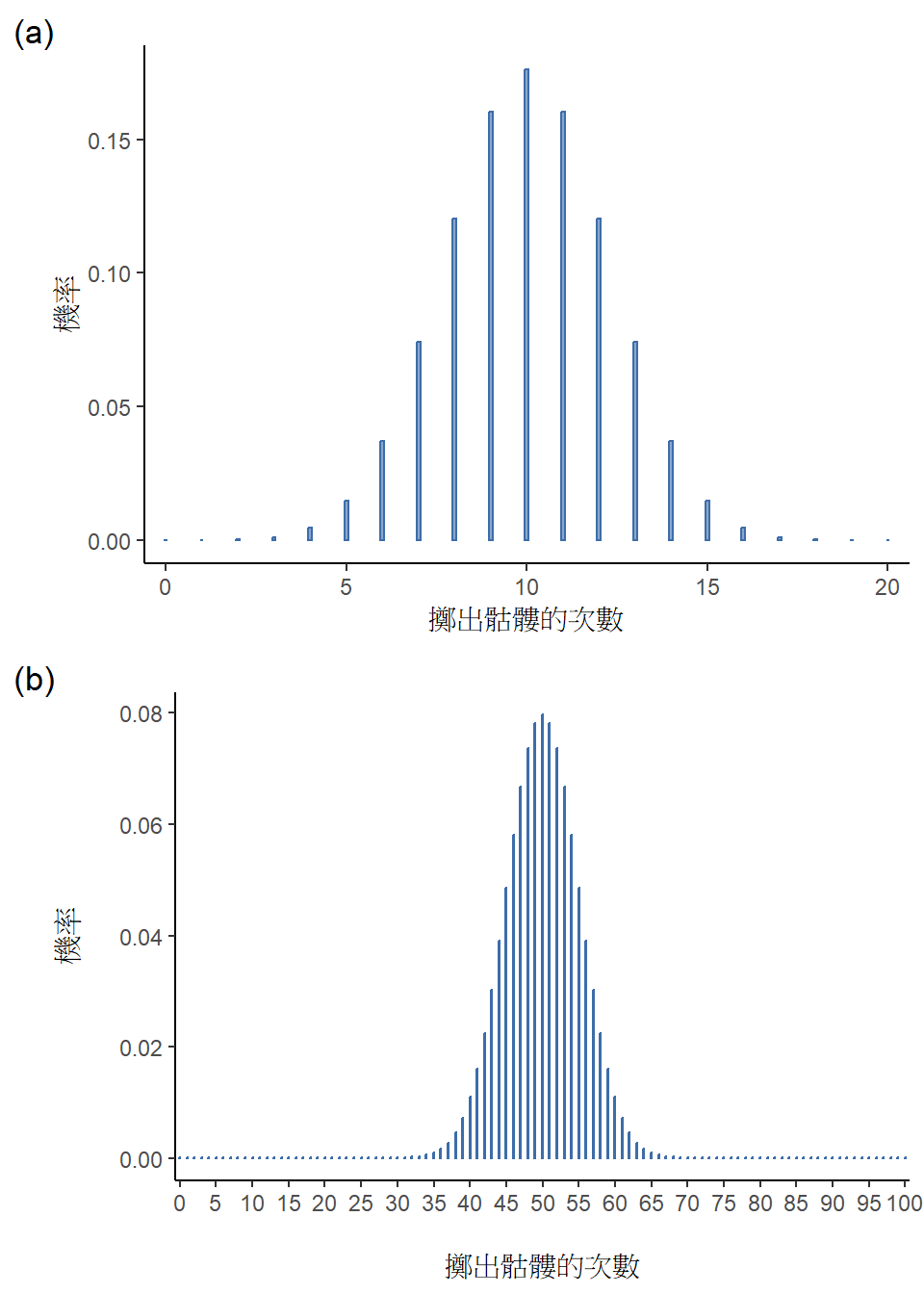
因為二項分佈柱狀圖的形狀會隨\(\theta\) 和 \(N\)改變,為了讓讀者好好感受,現在我們把實驗材料改成一面是骷髏頭像硬幣。這次的實驗是持續投擲一枚公平的硬幣,我會紀錄會有幾次骷髏的那面朝上,所以設定這個實驗每次結果的成功機率\(\theta = \frac{1}{2}\),做完實驗一共擲硬幣 \(N = 20\) 次。只有成功機率改變的話,二項分佈有會有什麼變化?你有稍微研究一下公式的話,會預期如 圖 7.4 (a) 展示的柱狀圖一樣,分佈的中心點位置移動到水平軸中央了。那麼連續擲\(N = 100\) 次呢? 如同 圖 7.4(b) ,分佈依然位於中間,但是可能的實驗結果(柱子)數量增加了。
7.5 常態分佈
雖然二項分佈是最好懂的機率分佈,不過並不是統計學裡最重要的分佈,運作各種統計方法要依賴的其實是常態分佈,又稱“鐘形曲線”或“高斯分佈”。常態分佈用兩個參數描述分佈的形狀:平均值 μ 和標準差\(\sigma\)。用隨機變數符號 \(X\) 來表現的話就是:
\[X \sim \text{Normal}(\mu,\sigma)\]
[附加技術細節 8]
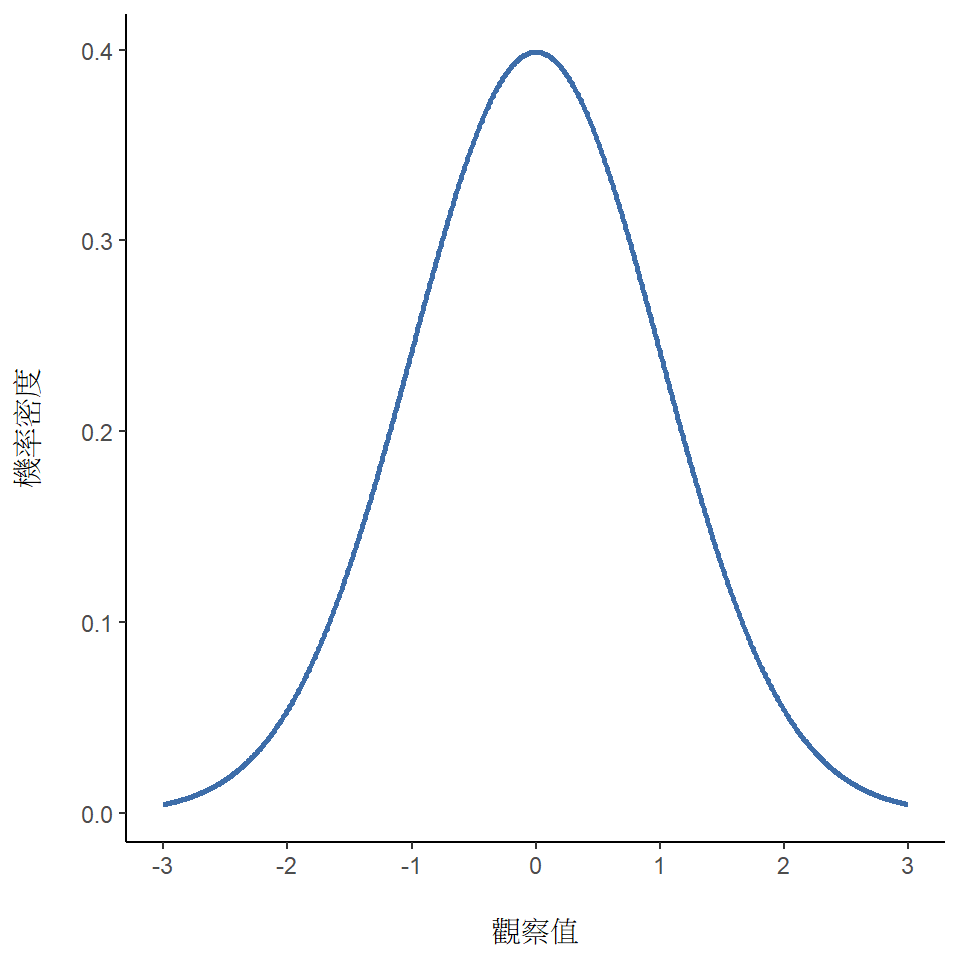
接著來談談為何常態分佈的視覺化長得如同 圖 7.5 的樣子。圖中的常態分佈參數是平均值 \(\mu = 0\) 、標準差 \(\sigma = 1\) 。從外形就能了解又稱為“鐘形曲線”的原因;真得看起來有點像中世紀時期的鐘。那麼常態分佈和二項分佈有何不同?首先 圖 7.5 的常態分佈呈現光滑的曲線,而不是“柱狀圖”。這不是隨便畫的,因為常態分佈是連續隨機變數,而二項分佈是離散隨機變數。用上一節的擲骰子範例來解釋的話,每次會獲得3個骷髏或4個骷髏,但是不可能會獲得3.9個骷髏。如同 圖 7.3 呈現的事實:\(X = 3\) 有一個長條, \(X = 4\) 處也有一個長條,但是兩者之間没有。連續隨機變數没有這樣的限制。以天氣溫度來說,某個春天的日子氣溫可能是23度、24度、23.9度、或介於任兩個數值之間的任何數字,因為溫度是連續變數。這也是為什麼,常態分佈很適合描述春季的氣溫9。
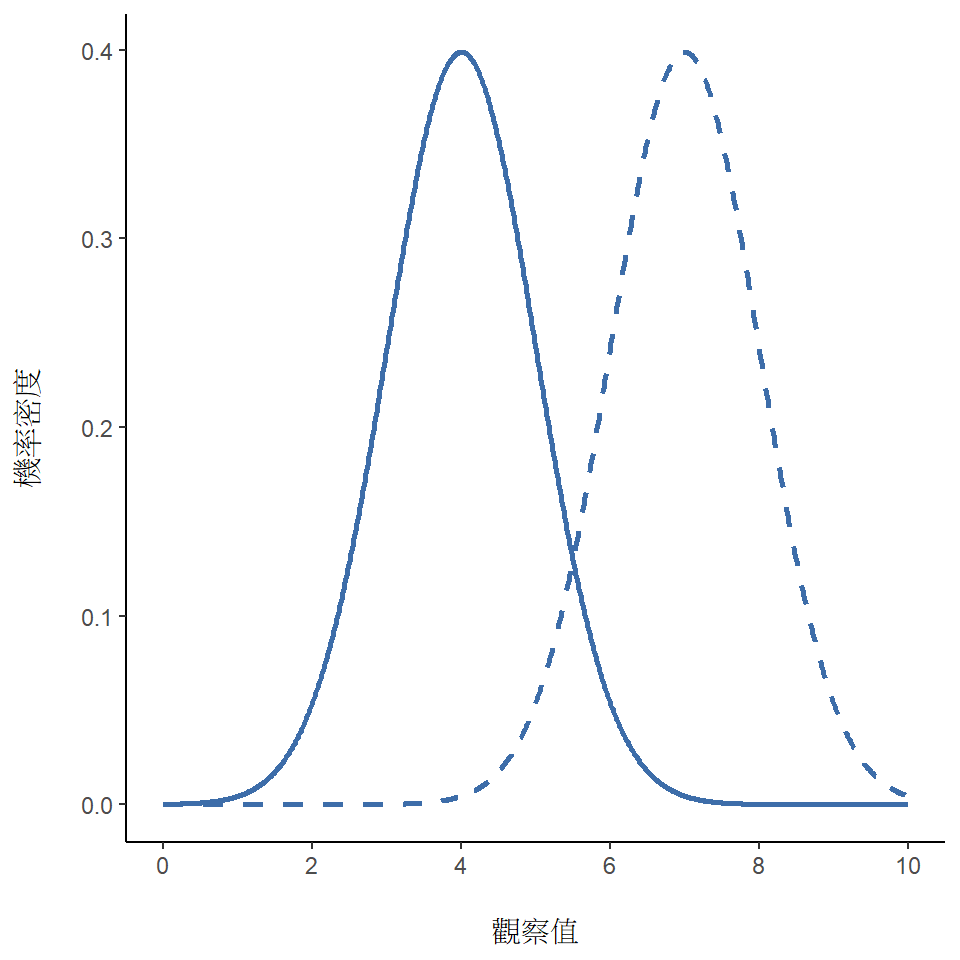
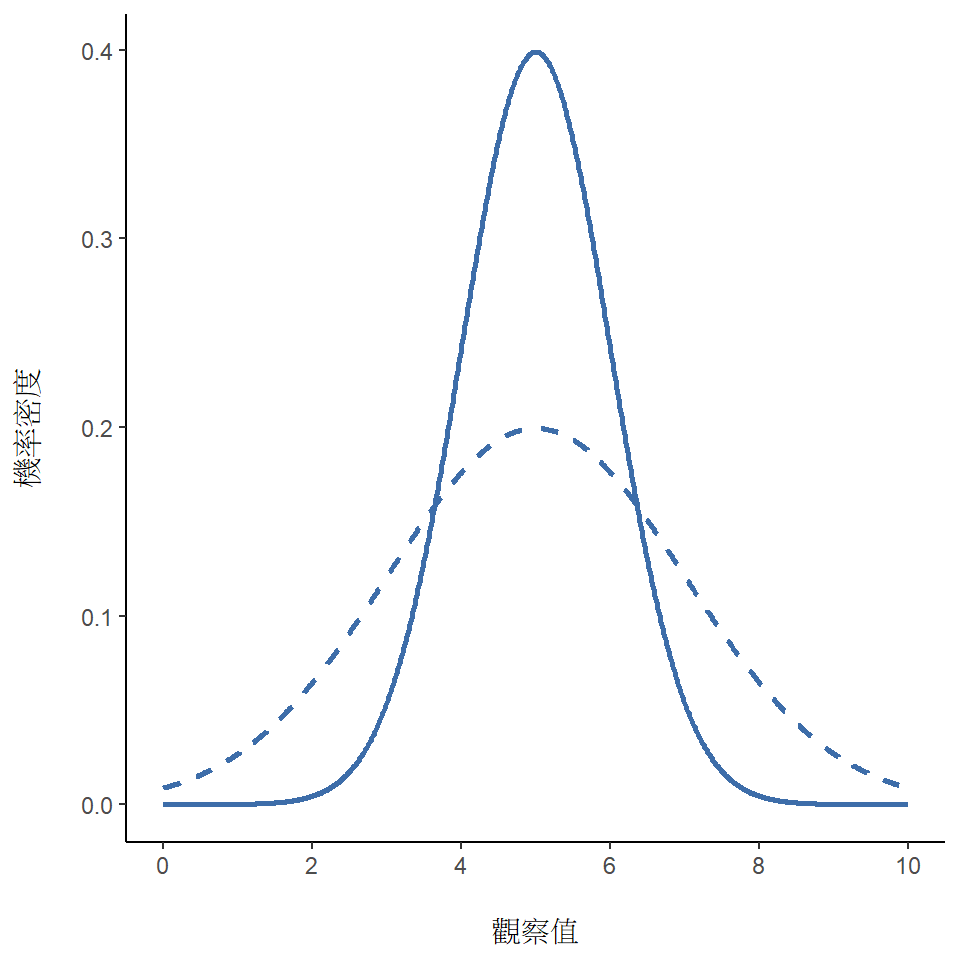
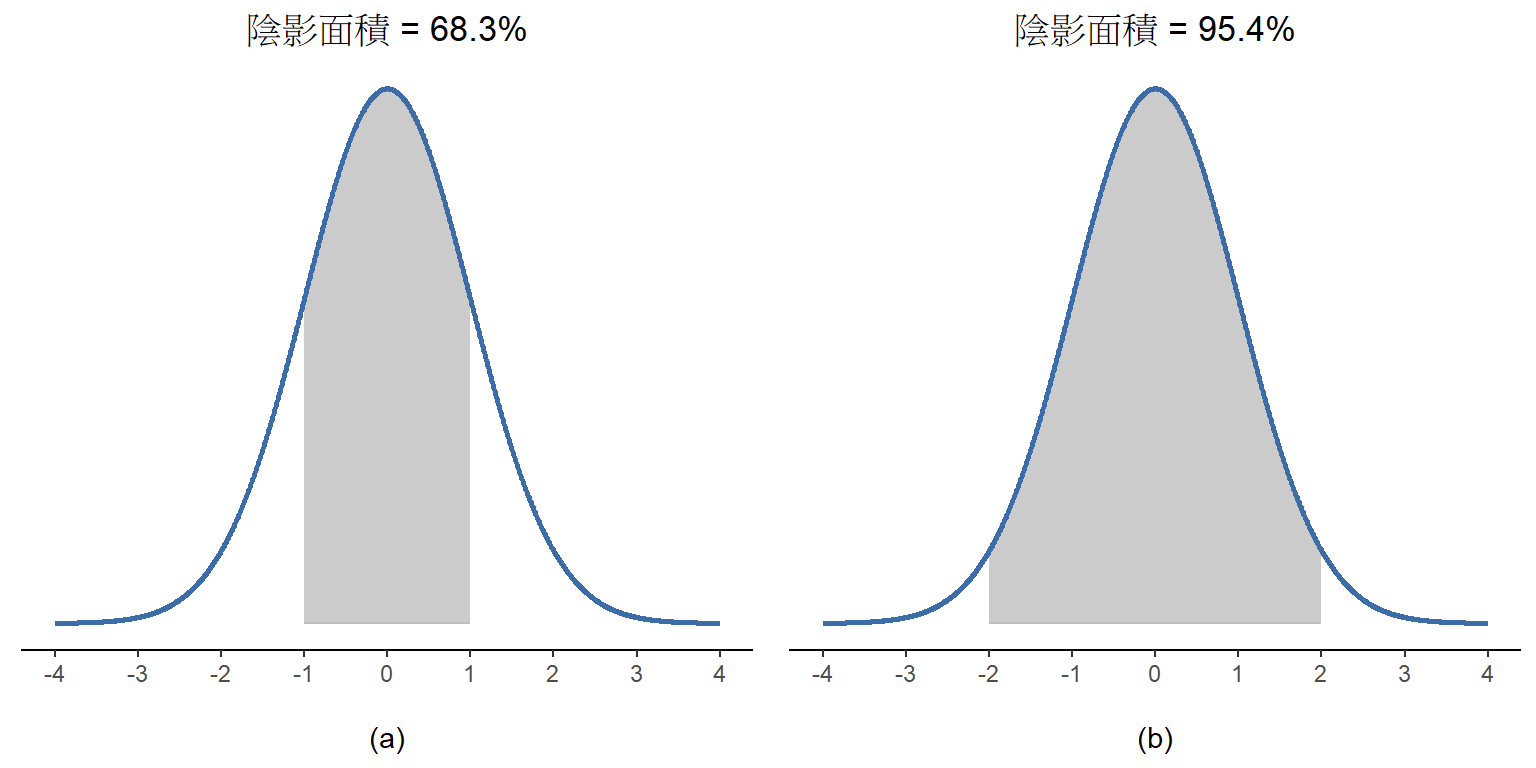
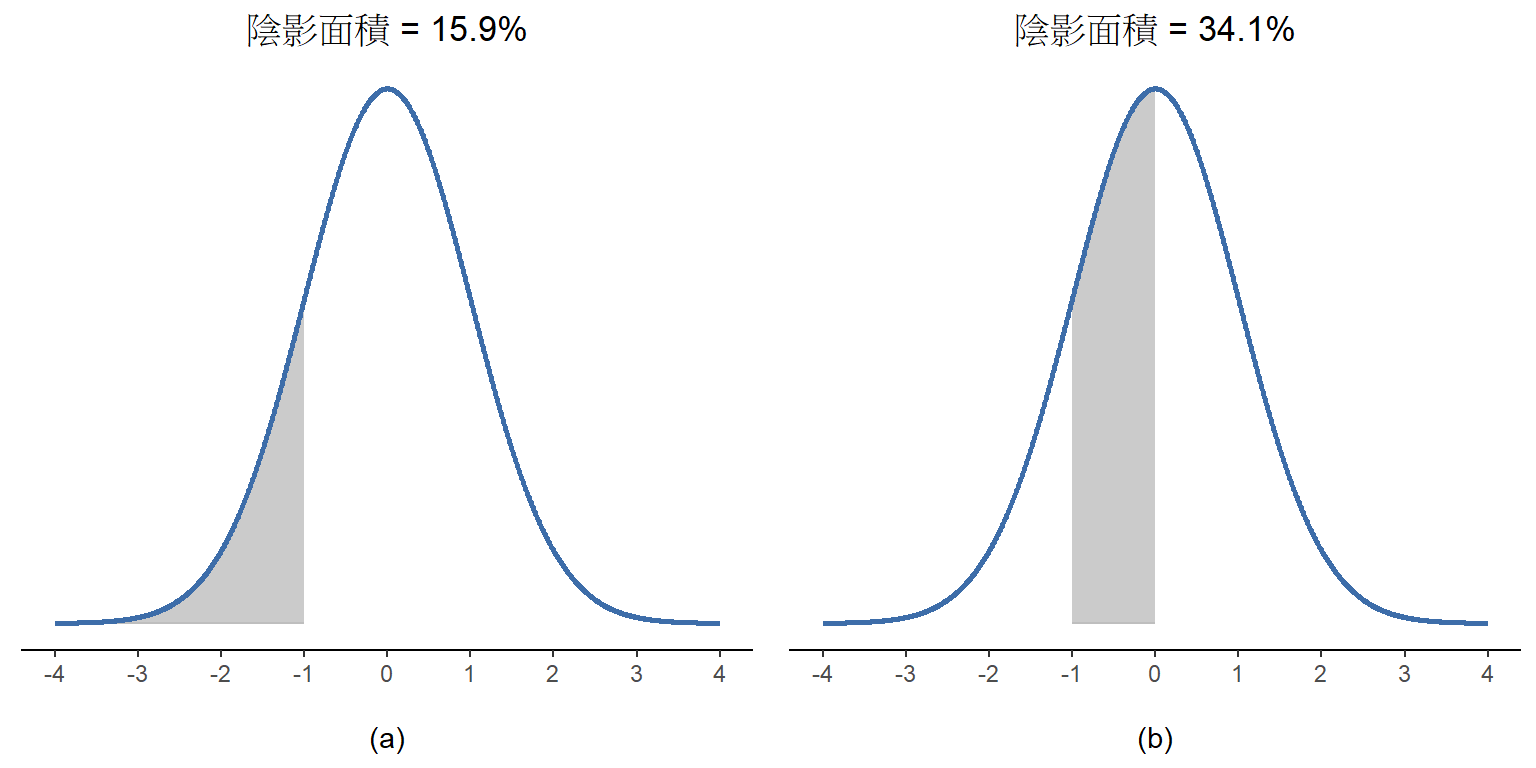
讓我們試著用直觀的方式瞭解常態分佈為何是連續隨機變數,首先看一下改變分佈的參數會改變什麼。圖 7.6 並列平均值不同,但是標準差相同的常態分佈。讀者可以預期兩個分佈都具有相同的“寬度”,唯一區別是其中一個的最高點在左邊、另一個在右邊。兩者的其他特徵都是相同的。如果保持平均值不變、增加標準差的話,新的分佈最高點還是在同樣的位置,不過分佈曲線變得更寬,如同 圖 7.7 的展示。留意一下分佈寬度變大時,最高點的高度會跟著降低。這是必然的,如同離散二項分佈的所有柱子,高度相加起來必須為1,常態分佈曲線覆蓋的面積也必須等於1。 除此之外,常態分佈還有一個重要特徵需要讀者知道:無論實際平均值和標準差是多少,從平均值向左右延伸1個標準差覆蓋了 \(68.3\%\) 的面積;從平均值向左右延伸2個標準差覆蓋了 \(95.4\%\) ;從平均值向左右延伸3個標準差覆蓋了 \(99.7\%\) 。 請參考 圖 7.8 和 圖 7.9 的說明。
7.5.1 機率密度
以上常態分佈的介紹之中,其實一直避而不談機率密度,許多基礎統計教科書也會省略不提。不談機率密度也是是對的,因為這概念的本質既奇怪又違反多數人的直覺,雖然現代統計方法的許多使用標準是採用機率密度設定的。幸好如果謮者只是想要學完基礎統計的所有內容,有沒有弄懂機率密度並非必要,只有之後要學習更進階的統計課程才有必要。如果讀完這一節還是弄不懂的話也不必灰心,就算只記得一部分內容,也能讓你更能掌握如何學習使用各種統計方法
在介紹常態分佈的視覺化統計圖裡,讀者可能已經注意到這些圖中的 y 軸標記為“機率密度”而不是密度。還有若是有仔細看常態分佈公式的話,應該會注意到符號是 \(p(X)\) 而不是 \(P(X)\)。
這是因為圖中呈現數值的並不是實際的機率,而是某種代理指標。要理解那些y軸的數值是什麼意思,需要花一些時間了解 \(X\) 是連續隨機變數是什麼意思。比如我們正在聊現在戶外氣溫有幾度。溫度計顯示 \(23\) 度,但我知道這並不是真的。因為不是剛好 \(23\) 度,我心裡想也可能是 \(23.1\) 度。但我知道這也並不是真的,因為它實際上可能是 \(23.09\) 度。但是我知道……好啦,我講這麼一大串,是讓你了解連續隨機變數的真正棘手之處是,沒有工具能測出準確的數值。
現在來想一想如何計算連續隨機變數的機率。假設要預測明天的最高溫度,就從從平均值為 \(23\) 度、標準差為 1 的常態分佈中隨機選出一個數值。溫度正好是 \(23\) 度的機率是多少?答案是“零”,或者可能是“一個如此接近零以至於可以視為零的數字”。為什麼會這樣?這就像往一個無限小的飛鏢靶心丟飛鏢。無論你多會瞄準,你永遠不會命中(除非你是某個娛樂作品的主角)。在現實生活中,永遠不會出現剛好是 \(23\) 度的值,真實數值總是會像 \(23.1\) 或 \(22.99998\)等一類的數值。換句話說,想要知道溫度正好是 \(23\) 度的機率是多少是完全没有意義的。然而,日常的溝通我跟你說戶外是 \(23\) 度,就算實際上是 \(22.9998\) 度,你也不會認為我在騙你。因為在日常溝通的情境,\(23\) 度通常涵蓋“ \(22.5\) 度及 \(23.5\) 度之間的某個位數值”。雖然計較溫度正好是 \(23\) 度的機率沒有不太意義,但是評估溫度在 \(22.5\) 度和 \(23.5\) 度之間,或者 \(20\) 度和 \(30\) 度之間,或者任何兩個數值範圍之間的機率相當合理。
這段討論的重點是,當我們使用連續機率分佈時,計算某個特定值的機率並没有意義。然而,我們可以評估某個數值落在那段數值範圍內的機率。為了找出某個數值範圍的機率,要做的就是計算“曲線下的面積”。我們已經在 圖 7.8 看到這個概念的視覺化,其中顯示的陰影區域代表真實機率,像是其中的圖(a)顯示了觀察到的值落在離平均值 1 個標準差範圍內的機率。
到這裡已經解釋了一部分被省略的情節,以上說明了為何知道一段數值範圍覆蓋的曲線下面積,是解讀連續機率分佈的面積關鍵。那麼這一節開始提到的 \(p(x)\) 在 公式裡是什麼角色?很 顯然\(p(x)\) 不是代表一個機率值,那究竟是什麼?這個符號 \(p(x)\) 的正式名稱是機率密度。在這個單元展示的曲線圖,就是y軸的數值,對應曲線的高度。密度本身並没有任何意義,但是經過“調整”,就可確保曲線下的部分面積可以代表真實機率。老實說,這就是現在你需要學習有關機率密度的全部知識。10
7.6 其他常見機率分佈
常態分佈是統計學最常使用的機率分佈(原因很快就會討論),二項分佈在很多狀況也會用到。 因為使用統計都是遇到各式各樣機率分佈,我們將在後面的單元會遇到其中一些。 特別是另外三個還沒介紹的t 分佈、\(\chi^2\) 分佈和 F 分佈。 我也不會跟你解釋這些分佈的公式,也不會多寫幾段話討論這些分佈,讀者只要透過這些視覺化圖像感受他們:圖 7.10、圖 7.11 和 圖 7.12。
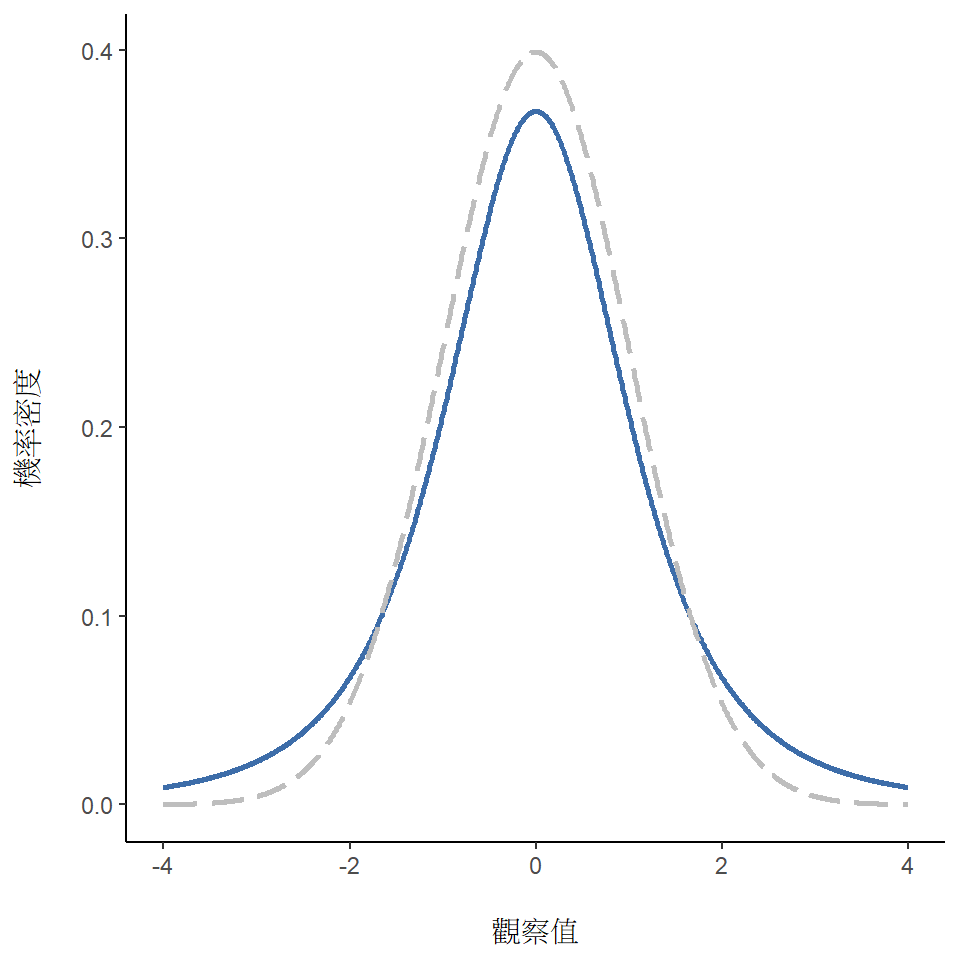
- t 分佈是一種與常態分佈非常相似的連續分佈,請見 圖 7.10。 仔細看t 分佈的“尾巴”比常態分佈的尾巴更“重”(尾巴曲線稍微高一些)。這是兩者之間的重要區別,當你認為資料的分佈符合常態分佈但並不知道平均值或標準差,其實應該是符合t分佈。 單元 11 將學習使用t分佈的統計分析方法。

- \(\chi^2\) 分佈也是經常在許多文獻報告裡看到的機率分佈。 最常使用的場景是 單元 10 介紹的分類資料分析,實際上這個分佈無處不在。如果讀者有興趣深入研究機率分佈的數學原理(如果你上完這個課程開竅的話?),會發現 \(\chi^2\) 分佈隨處可見的主要原因是,如果要處理不只一個符合常態分佈的變項,計算出平方和之總和後(稱為計算“平方和”),形成的隨機變數就是 \(\chi^2\) 分佈。知道這個原理會提昇你運用統計的能力。 現在先感受一下 \(\chi^2\) 分佈的視覺特徵: 圖 7.11。
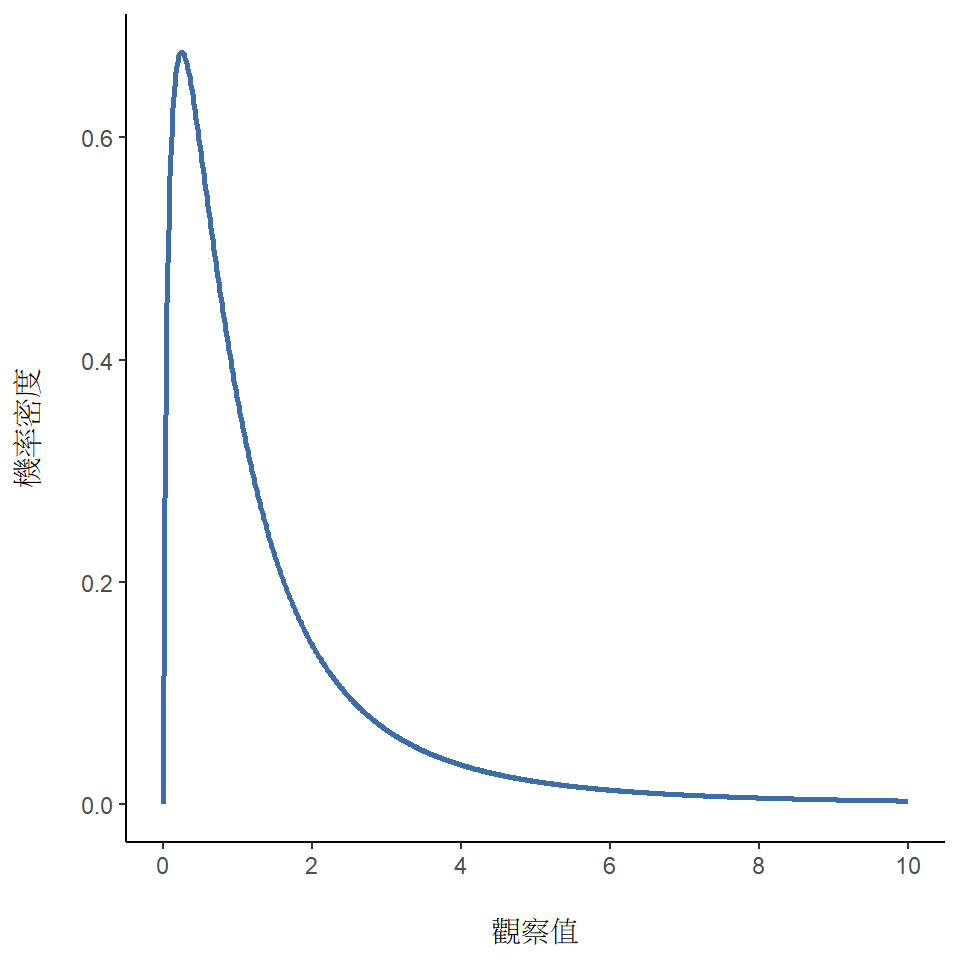
- F 分佈看起來有點像 \(\chi^2\) 分佈,並且需要比較個 \(\chi^2\) 分佈就會遇到。 雖然任何有頭腦的人都不會想挖這個坑跳進去,但這種比較在資料分析實務非常重要。 還記得 \(\chi^2\) 分佈是處理“平方和”會用到的機率分佈嗎?這也就是說如果要處理的統計問題是比較兩個“平方和”,就要使用F分佈。當然,我們目前還沒遇到有平方和的範例,這是 單元 13 的學習課題,我們將在那個單元好好認識F分佈。現在請看 圖 7.12 感受F分佈的特徵。
這個單元終於要結束了。讀者們又看到三種機率分佈:\(\chi^2\)、t 和 F。 這些都是連續分佈,並且都與常態分佈有密切關聯。不想深究數學原理的讀者,只要知道這些基本事實就足夠了。在後面的單元,我們將遭遇遵循常態分佈或至少假定遵循常態分佈的資料。讀者現在只要記住,如果假定要處理的資料遵循常態分佈,其實應該使用\(\chi^2\)、t 或 F 分佈的話,不必感到驚慌了。
7.7 本章小結
在本章中,我們討論了機率。我們討論了機率的意義以及為什麼統計學家無法就其意義達成共識。我們討論了機率必須遵守的規則。並且我們介紹了機率分佈的概念,並在本章中花了很大篇幅討論統計學家使用的一些更重要的機率分佈。逐節概述如下:
如您所料,我的內容絕不詳盡。機率論本身就是數學的一個巨大分支,與其在統計和資料分析中的應用完全分開。因此,這個主題上已經寫了上千本書,大學通常提供多門完全致力於機率論的課程。即使是記錄標準機率分佈這樣“更簡單”的任務也是一個大課題。我在本章中描述了五種標準機率分佈,但在我的書架上有一本45章的書,名為“統計分佈” (Evans et al., 2011),其中列出了很多更多分佈。幸運的是,您需要的很少。當您走出去做現實世界的資料分析時,您不太可能需要知道幾十種統計分佈,在本書中您肯定不需要它們,但是瞭解還有其他可能性永遠不會有害。
關於最後一點,在某種意義上,整章可以說是額外的內容。許多本科心理學統計課程會很快減少這部分內容(我知道我的課程就是這樣),即使是更高級的課程也經常會“忘記”重新訪問該領域的基礎。大多數學術心理學家不會區分機率和密度,直到最近,很少有人意識到貝式和次數主義機率之間的區別。然而,我認為在繼續應用之前理解這些很重要。例如,在進行統計推論時,有很多關於您“允許”說什麼的規則,其中許多看起來很武斷和奇怪。然而,如果您瞭解貝式與次數主義的區別,它們就會變得有意義。同樣,在 單元 11 中,我們將談論所謂的 t 檢定,如果您真的想完全理解 t 檢定的機制,那麼瞭解 t 分佈的實際情況真的會有幫助。我希望您理解我的意思。
譯註~許多機率與統計的教科書或科普書,將frequentist翻成“頻率主義”。由於frequency在英文指涉事件發生的空間與時間,配合動詞時態,能在語境裡理解frequency是指空間或時間的事件變動。然而中文動詞無時態,英文原句的frequency如果沒有指涉時間的變化,直翻為”頻率”不但不夠精確,在許多語境還可能造成誤解。由於在行為科學的統計學應用場景,「時間」是較少被提及的因素,因此本書中文版以“次數主義”稱呼。在各單元的中文翻譯,會根據語境調整用詞。↩︎
這當然並不是說次數主義觀點的方法論不能做假設性陳述。只是如果您想使用機率模型表達假設,可能必須將假設的內容重新定義為潛在可觀測事件的次數序列,以及序列的各種結果的相對次數。↩︎
譯註~數學家版的貝氏定理\[Pr(A|B) = \frac{Pr(B|A)*Pr(A)}{Pr(B)}\] 統計學家版的貝氏定理\[Pr(H_i|Data) = \frac{Pr(Data|H_i)*Pr(H_i)}{\sum_{j=1}^n Pr(Data|H_j)*P r(H_j)}\] 兩套公式取自旗標出版AI 必須!從做中學貝氏統計。↩︎
請注意,這裡的“成功”是武斷的命名,並不是說出現這樣的結果是我所希望的。 如果 \(\theta\) 指的是某位機車騎士因為交通事故受傷的機率,我還是會用成功機率稱呼,但這並不是說我希望有人因為交通事故受傷!↩︎
請注意,這裡的“成功”是武斷的命名,並不是說出現這樣的結果是我所希望的。 如果 \(\theta\) 指的是某位機車騎士因為交通事故受傷的機率,我還是會用成功機率稱呼,但這並不是說我希望有人因為交通事故受傷!↩︎
如果讀者知道一點微積分,我會用一種稍微精確方式解釋。如同離散機率函數涵蓋所有事件的機率,其值為必為正數且總和為1,連續機率函數涵蓋範圍內非零的機率密度且總和也是1。要計算代表事件a與b之間所有數值的發生機率,只要以密度函數計算兩者之間機率密度所佔面積的積分\(\int_{a}^{b} p(x) dx\)。若是讀者從未學過或已經忘記微積分,請不用擔心這個,本書的材料不需要懂微積分也能學習。↩︎
二項分佈公式的 \(X!\) 代表階乘(將1到\(X\)的所有整數相乘):\[P(X | \theta, N) = \displaystyle\frac{N!}{X!(N-X)!}\theta^X(1-\theta)^{N-X}\] 如果這個公式對您來說没有太大意義,請不用擔心。 使用本書學習統計不需要知道這個公式。↩︎
如同二項分佈,在此列出常態分佈的隨機變數公式,是因為這非常重要,每個學習統計學的同學都應該至少看一眼。由于這是一本簡介教材,為了不做深入介紹,完整公式隱藏於這個脚注: \[p(X|\mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(X-\mu)^2}{2\sigma^2}}\]↩︎
常態分佈在統計分析實務非常好用,使得就算變數實際上並不是連續時,分析人員也會使用。只要構成結果變項的選項够多(像是很多問卷常用的李克特量表),以常態分佈作為近似的資料樣本分佈是相當標準的做法。這可能讓分析實務變得簡單。↩︎
如果讀者知道一點微積分,我會用一種稍微精確方式解釋。如同離散機率函數涵蓋所有事件的機率,其值為必為正數且總和為1,連續機率函數涵蓋範圍內非零的機率密度且總和也是1。要計算代表事件a與b之間所有數值的發生機率,只要以密度函數計算兩者之間機率密度所佔面積的積分\(\int_{a}^{b} p(x) dx\)。若是讀者從未學過或已經忘記微積分,請不用擔心這個,本書的材料不需要懂微積分也能學習。↩︎