14  多因子變異數分析

過去幾章已經探討了相當多的內容，我們探討過當研究中包含一個具有兩組（例如 單元 11 的t檢定）或三組以上（見 單元 13 ）的名義變項時，可以使用的統計檢定。 單元 12 介紹了一個強大的新概念：建立具有多個連續預測變項的統計模型，用以解釋單一的結果變項。舉例來說，迴歸模型可以根據學生投入學習的時數，以及他們在標準化智商測驗上的分數，來預測其在閱讀理解測驗中可能犯錯的次數。

這個單元的目標，是將使用多個預測變項的概念，延伸至變異數分析的架構。舉例來說，假設我們想利用閱讀理解測驗來評估三所不同學校學生的學習成就，同時我們也懷疑性別可能會影響學生的發展速度（因此預期不同性別的學生成績表現也會有差異）。在這種情況下，每位學生都會被兩個變項分類：一是「性別」，二是「學校」。我們希望能同時根據這兩個分組變項，來分析學生的閱讀理解分數。用來進行這種分析的工具，泛稱為因子設計變異數分析 (factorial ANOVA)。由於我們的設計中有兩個分組變項，因此也常稱為二因子變異數分析 (two-way ANOVA)，此名稱正好與 單元 13 所介紹的單因子變異數分析 (one-way ANOVA) 相對應。

14.1 平衡且無交互作用的因子設計分析

修改建議當我們在 單元 13 討論變異數分析時，我們是基於一個相對簡單的實驗設計。在該設計中，每位受試者會被分配到數個組別的其中一組，而我們想知道這些組別在某個結果變項上的平均數是否有所不同。本節將討論一類更廣泛的實驗設計，稱為因子設計 (factorial designs)，其中包含了多個分組變項。前文已舉過一個這類設計的例子，另一個例子則來自 單元 13 ，我們在其中探討了不同藥物對每位受試者情緒改善程度 (mood.gain) 的影響。在那一章中，我們確實發現藥物具有顯著效果，但章末的另一項分析卻顯示治療沒有效果。然而，這種為了預測同一個結果變項而執行兩次獨立分析的做法，其實有些令人憂慮。治療對於情緒改善 (mood.gain) 也許確實有效果，但我們之所以沒發現，會不會是因為它的效果被藥物的效果所「遮蔽」(hidden) 了呢？換句話說，我們需要執行一個單一分析，將「藥物」和「治療」同時納為預測變項。在這種分析中，每位受試者會依其服用的藥物 (一個有 3 個水平的因子) 與接受的治療 (一個有 2 個水平的因子) 來進行交叉分類。我們將這樣的設計稱為\(3 \times 2\)因子設計。

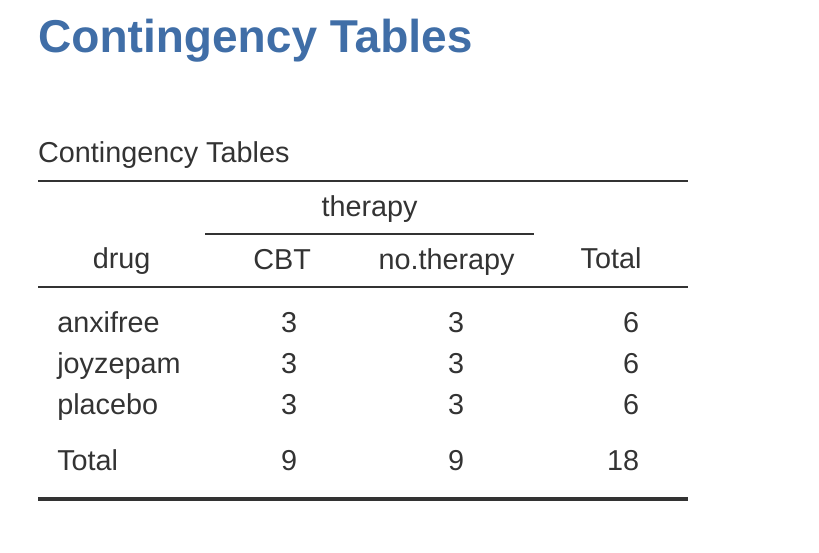
如果我們用jamovi的“次數分析”模組-“列聯表”(Contingency Tables)分析藥物和治療方式的效果（見 小單元 6.1），會得到 圖 14.1 的表格。

圖 14.1: 藥物與治療效果的列聯表

從列聯表中可見，本研究的設計不僅涵蓋了兩個因子的所有可能組合──這代表它是一個完全交叉 (completely crossed) 的設計──而且每個組別的受試者人數也完全相同。換句話說，這是一個平衡設計 (balanced design)。本節將先探討如何分析平衡設計的資料，因為這是最單純的情況。非平衡設計 (unbalanced designs) 的情況則相當繁瑣，因此我們暫時先不討論。

14.1.1 我們要檢定的是何種假設？

與單因子變異數分析 (one-way ANOVA) 類似，因子設計ANOVA 也是一種用來檢定特定母體平均數假設的工具。因此，一個合理的起點，便是明確地定義我們所要檢定的假設。然而，在此之前，我們有必要先建立一套簡潔的符號系統，用以描述母體平均數。由於觀測值是依據兩個不同的因子進行交叉分類，因此我們可能會對許多不同層次的平均數感興趣。為了理解這點，讓我們先思考一下，在這類設計中我們可以計算出哪些不同的樣本平均數。首先，最顯而易見的，就是我們會對 表 14.1 中所列出的各組平均數感興趣。

表 14.1:

clinicaltrial依藥物和治療方法分組的各組平均值

drug	therapy	mood.gain
placebo	no.therapy	0.30
anxifree	no.therapy	0.40
joyzepam	no.therapy	1.47
placebo	CBT	0.60
anxifree	CBT	1.03
joyzepam	CBT	1.50

表 14.2 列出了這兩個因子所有可能組合下的組別平均數。(例如：服用安慰劑且無治療的受試者、服用安慰劑並同時接受認知行為治療(CBT)的受試者等)如果我們將這些組別平均數，連同邊際平均數 (marginal means) 與總平均數 (grand mean)，一併整理成單一表格，將有助於我們理解。完整的表格如下所示：

表 14.2:

clinicaltrial依藥物和治療方法分組的總平均值

	no therapy	CBT	total
placebo	0.30	0.60	0.45
anxifree	0.40	1.03	0.72
joyzepam	1.47	1.50	1.48
total	0.72	1.04	0.88

當然，前面提到的這些平均數，都屬於樣本統計量 (sample statistic)。這個數值是根據我們在研究中所觀測到的特定資料計算而來。而我們真正想推論的，是與之對應的母體參數 (population parameters)。也就是存在於更廣泛母體中的真實平均數。這些母體平均數同樣可以整理成一個類似的表格 (見 表 14.3)，但需要借助一些數學符號來標示。依照慣例，我們會用 \(\mu\)代表母體平均數。然而，由於這裡有許多不同層次的平均數，因此需要使用下標 (subscripts) 來加以區分。

這套符號系統的運作方式如下。它基於一個由兩個因子所定義的表格：每一行對應因子 A (本例中為「藥物」) 的一個水平；每一列則對應因子 B (本例中為「治療」) 的一個水平。如果我們以 R 代表表格的總行數，C 代表總列數，便可以稱之為一個\(R \times C\)因子設計ANOVA。在本例中，\(R = 3\) 且 \(C = 2\)。接著，我們用小寫字母來指代特定的行與列，因此\(\mu_{rc}\)所代表的，就是因子\(A\)第\(r\)個水平 (即第\(r\)行) 與因子\(B\)第\(c\)個水平 (即第 c 列) 交叉組合下的母體平均數。¹所以現在母體的均值是寫成@tbl-tab13-1的形式：

表 14.3:

因子設計表各分組使用的母群參數符號

	no therapy	CBT	total
placebo	\( \mu_{11} \)	\( \mu_{12} \)
anxifree	\( \mu_{21} \)	\( \mu_{22} \)
joyzepam	\( \mu_{31} \)	\( \mu_{32} \)
total

那麼，表格中剩下的項目該如何理解？舉例來說，我們要如何描述「所有可能服用 Joyzepam 的(假設)母群，無論其是否接受 CBT 治療，其平均情緒改善程度」？我們會使用「點」標示法 (dot notation) 來表達這個概念。以 Joyzepam 為例，我們所關心的是與表格第三行 (row) 相關的平均數。換句話說，我們是將兩個細格平均數 (\(\mu_{31}\)與 \(\mu_{32}\)) 加以平均。這個平均後的結果，就稱為邊際平均數 (marginal mean)，在此例中記為 \(\mu_{3.}\)。同樣地，CBT 的邊際平均數對應的是表格中第二欄 (column) 的母體平均數，我們將它記為\(\mu_{.2}\)，因為這個數值是將所有列 (rows) 的資料加以平均 (或稱邊際化 (marginalising)²) 後得到的。如此一來，我們完整的母體平均數表格便可寫成如 表 14.4 的形式。

表 14.4:

因子設計表各獨變項處置使用的母群參數符號

	no therapy	CBT	total
placebo	\( \mu_{11} \)	\( \mu_{12} \)	\( \mu_{1.} \)
anxifree	\( \mu_{21} \)	\( \mu_{22} \)	\( \mu_{2.} \)
joyzepam	\( \mu_{31} \)	\( \mu_{32} \)	\( \mu_{3.} \)
total	\( \mu_{.1} \)	\( \mu_{.2} \)	\( \mu_{..} \)

現在我們有了這套標示法，便可以輕易地建構並陳述假設。假設我們的目標是探討兩個問題：第一，藥物選擇是否對情緒有影響？第二，CBT 治療是否對情緒有影響？當然，這些並非我們能建構的全部假設 (我們將在 小單元 14.2 看到一個非常重要的不同案例)，但這兩個假設是最容易檢定的，因此我們先從這裡開始。

先考慮第一個檢定，也就是藥物的效果。如果藥物沒有效果，那麼我們便會預期所有代表不同藥物的行平均數 (row means) 都相同。這就是我們的虛無假說。反之，如果藥物確實有效果，我們則會預期這些行平均數會有所不同。在形式上，我們將此假說寫為：

虛無假說 \(H_0\)：所有行平均數皆相等，即 \(\mu_{1. } = \mu_{2. } = \mu_{3. }\)

對立假說 \(H_1\)：至少有一個行平均數與其他不同

值得注意的是，這與我們在 單元 13 ，對這筆資料進行單因子變異數分析時所建構的統計假設完全相同。當時，我們用 \(\mu_{P}\) 符號代表安慰劑組的平均情緒改善程度，並以 \(\mu_{A}\) 和 \(\mu_{J}\) 分別代表兩種藥物的組別平均數，其虛無假說為 \(\mu_{P} = \mu_{A} = \mu_{J}\)。所以，我們談論的其實是同一個假設，只是因為現在有多個分組變項，更複雜的變異數分析需要更嚴謹的標示法，才將此假設改寫為 \(\mu_{ 1.} = \mu_{ 2.} = \mu_{ 3.}\)。然而，讀者很快就會看到，儘管假說內容相同，但由於我們現在考量了第二個分組變項的存在，對此假說的檢定方式會有些微的差異。

接著談到另一個分組變項（心理治療方法），讀者大概不會對此感到意外：我們的第二個假說檢定，也是用同樣的方式建構。然而，由於我們在此討論的是心理治療而非藥物，因此我們的虛無假說所對應的，便是列平均數 (column means) 的相等性：

虛無假說 \(H_0\)：所有列平均數皆相等，即 \(\mu_{.1} = \mu_{.2}\)

對立假說 \(H_1\)：列平均數不相等，即 \(\mu_{.1} \neq \mu_{.2}\)

14.1.2 使用jamovi完成多因子變異數分析

上一節描述的虛無假說與對立假說，讀者應該會感到相當熟悉。它們基本上與我們在 單元 13 中，對更簡單的單因子變異數分析所檢定的假說相同。因此，讀者可能會預期因子設計ANOVA所使用的假說檢定，在本質上会與 單元 13 的 F 檢定相同。讀者會預期看到書中提及平方和 (SS)、均方 (MS)、自由度 (df)，以及最終能轉換為 p 值的 F 統計量。嗯，你會這樣想的話完全符合傳統的學習脈絡。正因如此，本書接下來將一反常態。在本書中，一般的做法是先描述特定分析背後的邏輯 (以及部份數學原理)，接著才介紹 jamovi 的操作。但這一次，我們要反過來，先示範如何在 jamovi 中執行分析。這麼做的目的，是為了強調在 單元 13 中所討論的單因子變異數分析，與我們將在本章使用的更複雜方法之間的相似之處。

若讀者要分析的資料屬於平衡因子設計，那麼執行變異數分析將會非常簡單。為了讓讀者感受其簡易之處，讓我們先重現 單元 13 中的分析。回顧先前的分析，當時我們只用了一個因子 (即「藥物」) 來預測結果變項 (mood.gain)，並得到如 圖 13.2 所示的結果。

我在上一節中描述的虛無假設和替代假設應該讓你感到非常熟悉。它們基本上與我們在 單元 13 中執行的更簡單的單因素ANOVA檢驗相同。所以你可能期望因子ANOVA中使用的假設檢驗本質上與 單元 13 中的F檢驗相同。您期望看到對平方和（SS）、平均平方（MS）、自由度（df）以及最終可以將之轉換為p值的F統計量的引用，對吧？好吧，你絕對是對的。 這麼多，以至於我要改變我的常規方法。在本書中，我通常採用先描述特定分析的基礎邏輯（在某程度上還有數學），然後再介紹jamovi中的分析的方法。這次我要相反地做，先告訴你如何在jamovi中執行它。這樣做的原因是我想強調 單元 13 中討論的簡單的單因素ANOVA工具，以及我們將在本章中使用的更複雜的方法之間的相似之處。

如果您試圖分析的數據對應於平衡的因子設計，那麼執行方差分析就很容易。要了解它有多容易，讓我們先重現 單元 13 中的原始分析。以防你忘了，對於那個分析，我們只使用一個因素（即藥物）來預測我們的結果變量（即mood.gain），並且得到了 圖 14.2 中顯示的結果。

圖 14.2: 藥物對情緒改善程度的單因子變異分析

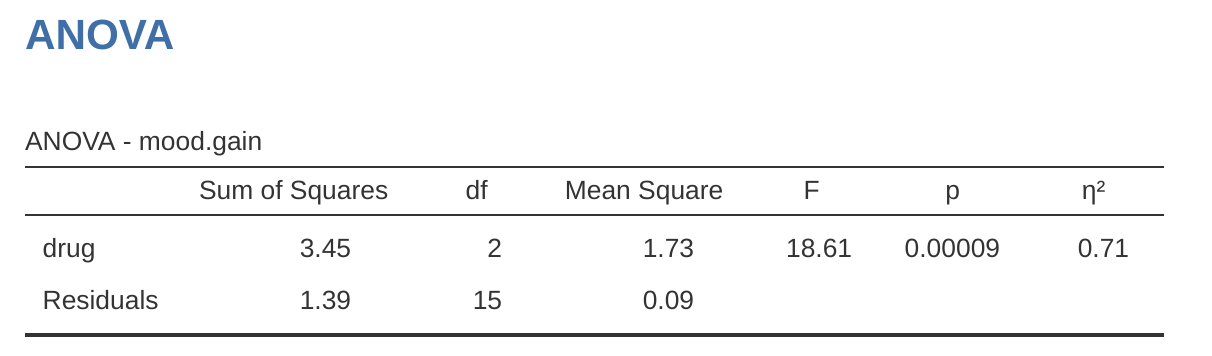
現在，假設我們也想探討「心理治療」是否與情緒改善程度 (mood.gain) 有關。回顧我們在 單元 12 中對多元迴歸的討論，讀者大概不會感到意外：我們所需要做的，就只是在分析中將「治療」新增為第二個「固定因子 (Fixed Factor)」，如 圖 13.3 所示。

圖 14.3: 藥物和心理治療對情緒改善程度的雙因子變異數分析

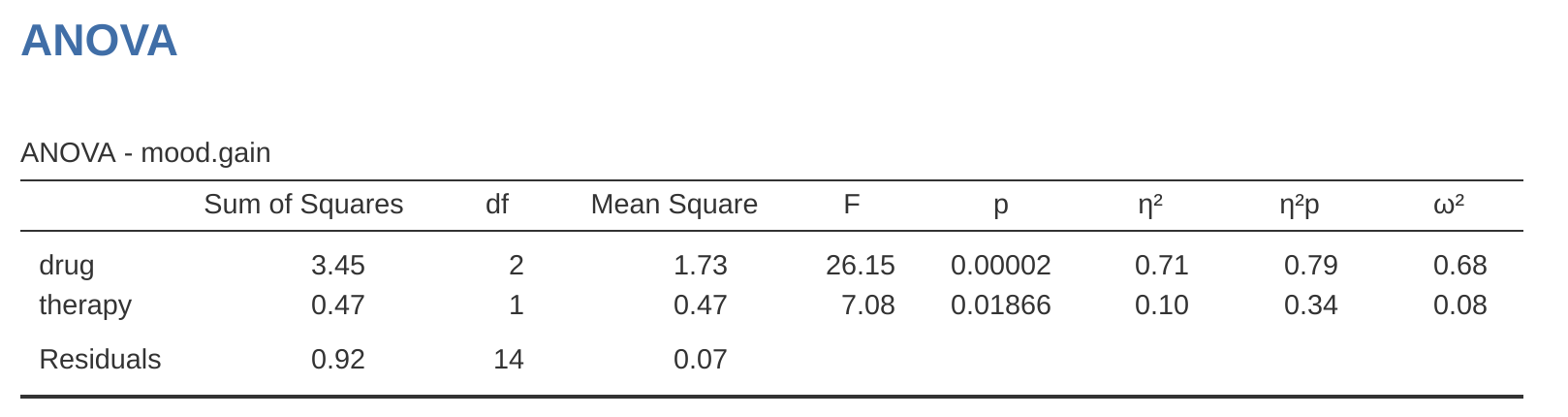
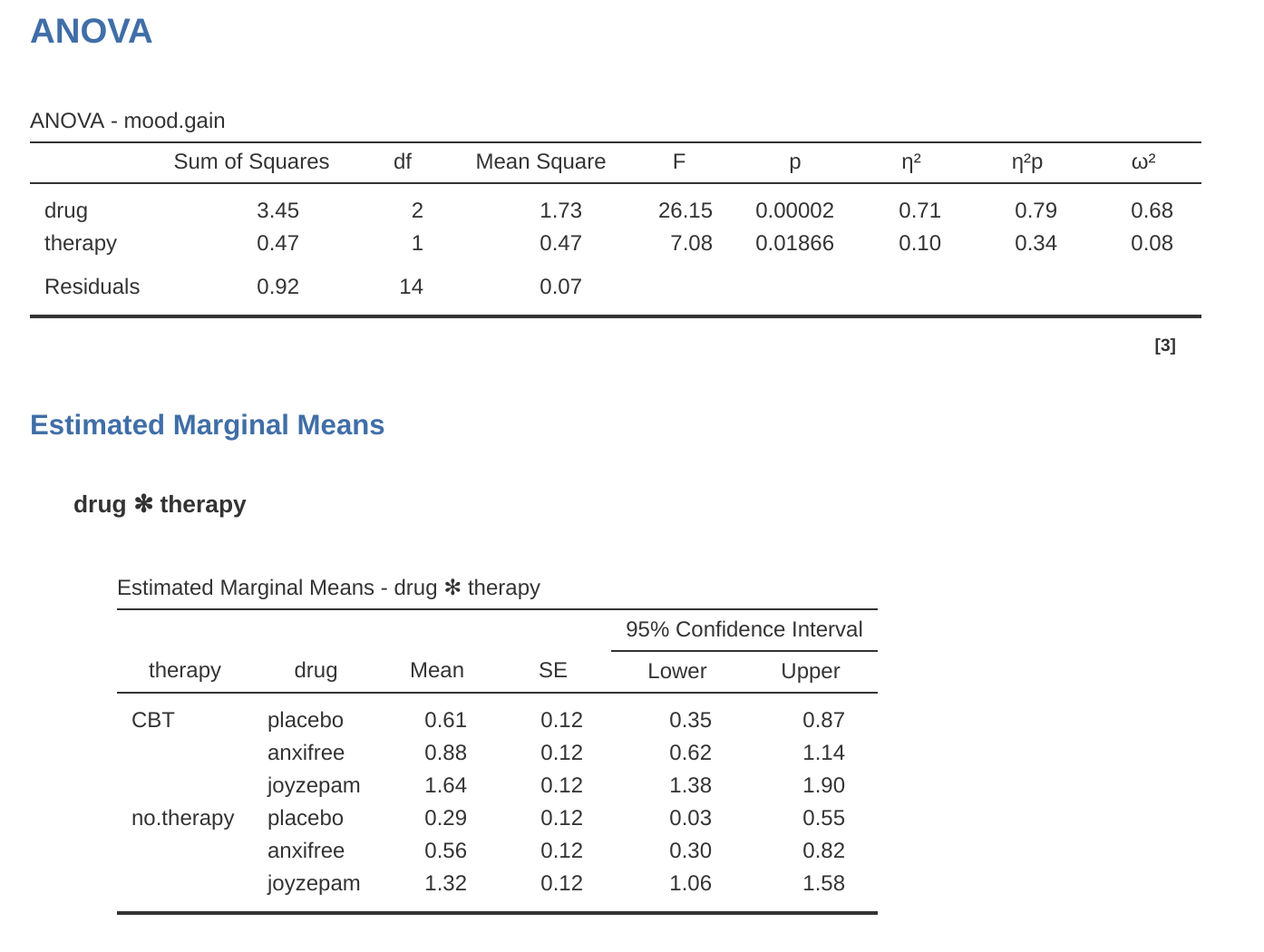
這份 jamovi 的輸出結果同樣很容易解讀。表格的第一列出了與「藥物」因子相關的組間平方和 (between-group SS)，以及其對應的組間自由度(df)。它同時也計算出平方和平均 (MS)、F 統計量及p 值。此外，表格中也分別有對應「治療」因子及殘差 (residuals) (即組內變異) 的列。

不僅這些個別的數值我們都很熟悉，它們之間的關係也維持不變，就如同我們在最初的單因子變異數分析中所見。請注意，平方和平均 (MS) 的計算方式，依然是將平方和 (SS) 除以其對應的自由度 (df)。也就是說，無論我們討論的是「藥物」、「治療」還是「殘差」，這個公式都成立：

\[MS=\frac{SS}{df}\]

為了驗證這點，我們暫時不必擔心平方和 (SS) 的數值是如何算出的，先當作 jamovi 已正確算好，來驗證表格中其餘的數值是否合理。首先，看到「藥物」因子，我們將 \(3.45\) 除以 \(2\)，便得到平方和平均為 \(1.73\)。至於「治療」因子，其自由度只有 1，計算更為簡單：將 \(0.47\) (SS值) 除以 1，即得到 \(0.47\) (MS值)。

接著看到 F 統計量與 p 值，讀者會注意到這兩者各有兩個：一個對應「藥物」因子，另一個則對應「治療」因子。無論是哪個因子，其 F 統計量的計算方式，都是將該因子的平方和平均，除以殘差的平方和平均。如果我們用「A」簡稱第一個因子 (因子 A，本例中為「藥物」)，並用「R」簡稱殘差 (residuals)，那麼因子 A 的 F 統計量便可記為 \(F\_A\)，其計算方式如下：

\[F_A=\frac{MS_A}{MS_R}\]

這個公式也同樣適用於因子 B (即「治療」)。這裡用「R」來代表殘差是有點尷尬， क्योंकि我們也曾用 R 代表表格的行數。不過，「R」僅會在殘差平方和 (\(SS\_R\)) 與殘差平方和平均 (\(MS\_R\)) 的脈絡中代表殘差，因此應不致混淆。總之，用這道公式計算「藥物」因子的統計值，就是將平方和平均 1.73 除以殘差的平方和平均 0.07，就能得出 F 統計量為 26.15。同理，計算「治療」因子的統計值，是將 0.47 除以 0.07，得到 F 統計量為 7.08。這些數值與 jamovi 輸出的 ANOVA 表格裡的數值完全相同。

ANOVA 表格中也包含了 p 值的計算。同樣地，這裡的概念也沒什麼新奇之處。對於這兩個因子，我們的目標都是檢定「該因子與結果變項之間沒有關係」的虛無假說 (稍後會對此有更精確的說明)。為此，我們顯然遵循了與單因子變異數分析類似的策略，為每一個假說都計算出一個 F 統計量。要將 F 統計量轉換為 p 值，只需了解在虛無假說 (即該因子無關緊要) 成立的情況下，F 統計量的抽樣分佈會是 F 分布 (F distribution)。此外也需注意，計算時所需的兩個自由度，分別來自因子本身以及殘差。以「藥物」因子為例，我們使用的是具有 2 和 14 自由度的 F 分布 (自由度的細節稍後會詳述)。相對地，「治療」因子所對應的抽樣分佈，則是具有 1 和 14 自由度的 F 分布。

至此，讀者應該可以理解，解讀這種更複雜的因子設計分析的 ANOVA 表格，其方式與解讀較簡單的單因子分析表格大致相同。簡言之，這個 \(3 \times 2\) 設計的因子設計ANOVA 結果告訴我們：「藥物」有顯著效果 (\(F_{2,14} = 26.15, p \< .001\))，「治療」同樣也有顯著效果 (\(F\_{1,14} = 7.08, p = .02\))。或者，換個更精確的技術術語來說，我們會稱「藥物」與「治療」各有一個主要效果 (main effect)。目前將這些效果稱為「主要」效果，似乎有些冗贅，但這麼做其實是有道理的。稍後，我們將會討論兩因子之間可能存在的「交互作用 (interaction)」，因此我們通常會區分主要效果與交互作用效果。

14.1.3 計算因子設計子變異數分析的平方差

前一節有兩個目標。第一，是為了展示執行因子設計ANOVA 的 jamovi 操作，與我們用於單因子變異數分析的方法幾乎相同，唯一的差別只有新增了第二個因子。第二，是為了呈現這個範例的 ANOVA 統計表，好讓讀者從一開始就明白，因子設計ANOVA 背後的基本邏輯與架構，和支撐單因子變異數分析的邏輯與架構並無二致。請讀者先記住這種感覺。會有這種感覺千真萬確，因為因子設計ANOVA 的建構方式，與較簡單的單因子變異數分析模型或多或少是相同的。只不過，一旦開始深究細節，這種熟悉感便會煙消雲散。在傳統的學習過程中，這種欣慰感通常會被一股想對統計教科書作者們咆哮的衝動所取代。

我們接著來看一些細節。前一節的解釋說明了主要效果的假設檢定是 F 檢定, 但並未展示平方和 (SS) 是如何計算的，也未明確說明如何計算自由度 (df)，儘管後者相對單純。假設目前只有兩個預測變項：因子 A 與因子 B。若以 Y 代表結果變項，那麼 \(Y\_{rci}\) 就代表 rc 組中第 i 位受試者的結果值 (亦即因子 A 的第 r 個水平/列，以及因子 B 的第 c 個水平/行)。因此，若以 \(\bar{Y}\) 代表樣本平均數，我們便能沿用先前的標示法來表示細格平均數、邊際平均數及總平均數。也就是說：\(\bar{Y}_{rc}\) 是因子 A 第 r 個水平與因子 B 第 c 個水平對應的樣本平均數；\(\bar{Y}_{r.}\) 是因子 A 第 r 個水平的邊際平均數；\(\bar{Y}_{.c}\) 是因子 B 第 c 個水平的邊際平均數；而 \(\bar{Y}_{..}\) 則是總平均數。換言之，我們的樣本平均數可以組織成與母群平均數相同的表格。以我們的臨床試驗資料為例，該表格如 表 14.5 所示。

表 14.5:

clinicaltrial的樣本平均值的符號標示

	no therapy	CBT	total
placebo	\( \bar{Y}_{11} \)	\( \bar{Y}_{12} \)	\( \bar{Y}_{1.} \)
anxifree	\( \bar{Y}_{21} \)	\( \bar{Y}_{22} \)	\( \bar{Y}_{2.} \)
joyzepam	\( \bar{Y}_{31} \)	\( \bar{Y}_{32} \)	\( \bar{Y}_{3.} \)
total	\( \bar{Y}_{.1} \)	\( \bar{Y}_{.2} \)	\( \bar{Y}_{..} \)

回顧先前表格中的樣本平均數，我們可以看到 \(\bar{Y}_{11} = 0.30\)、\(\bar{Y}_{12} = 0.60\) 等數值。在我們的臨床試驗範例中，「藥物」因子有 3 種處置，「治療」因子有 2 種處置，因此我們所要處理的，便是一個 \(3 \times 2\) 的因子設計ANOVA。然而，為了讓說法更具一般性，我們會說因子 A (行因子) 有 \(R\) 個水平，因子 B (列因子) 有 \(C\) 個水平，因此這裡執行的，便是一個 \(R \times C\) 的因子設計ANOVA。

[額外的技術細節³]

14.1.4 計算自由度的規則

自由度的計算方式，與單因子變異數分析非常相似。對於任一給定因子，其自由度等於其水平數減 1 (即行因子 A 的自由度為 \(R - 1\)，列因子 B 的自由度為 \(C - 1\))。因此，「藥物」因子的自由度為 \(df = 2\)，而「治療」因子的自由度為 \(df = 1\)。關於這個數字的計算原理，在稍後討論將 ANOVA 解釋為迴歸模型時 (見 小單元 14.6)，會有更清楚的說明。但目前，可以先採用自由度的簡易定義，亦即：

自由度 = 觀測數量的個數 - 限制條件的個數

因此，就「藥物」因子而言，我們觀測到 3 個獨立的組別平均數，但這些平均數受到 1 個總平均數的限制，因此其自由度為 2。殘差的計算邏輯相似，但並不完全相同。在本實驗中，觀測值總數為 18。而限制條件則有：1 個總平均數、加上「藥物」因子衍生的 2 個額外組別平均數、再加上「治療」因子衍生的 1 個額外組別平均數，因此殘差自由度為 14。寫成公式，即為 \(N\_{total} - 1 - (R - 1) - (C - 1)\)，可簡化為 \(N\_{total} - R - C + 1\)。

14.1.5 多因子與單因子變異數分析

既然已經了解因子設計ANOVA 的運作方式，便值得花點時間將其與單因子變異數分析的結果進行比較，因為這能讓我們更深刻地體會到，為何執行因子設計ANOVA 是明智之舉。在 單元 13 中，曾分別進行過兩次單因子變異數分析：一次是檢視不同「藥物」之間是否存在差異，另一次則是檢視不同「治療」之間是否存在差異。如 小單元 14.1.1 所見，單因子變異數分析所檢定的虛無假說與對立假說，實際上與因子設計ANOVA 所檢定的假說完全相同。

若更仔細地檢視 ANOVA 表格，會發現兩種分析中，各個因子所對應的平方和 (藥物為 3.45，治療為 0.92) 與自由度 (藥物為 2，治療為 1) 都是相同的。但兩者的結果卻不相同！最值得注意的是， 小單元 13.9 進行「治療」的單因子變異數分析，並未發現顯著效果 (p 值為 .21)。然而，當我們在二因子變異數分析的脈絡中檢視「治療」的主要效果時，卻得到了顯著的結果 (p = .019)。這兩種分析的結果顯然並不相同。

為什麼會發生這種情況？答案在於理解殘差的計算方式。回想 F 檢定的核心概念，便是比較「可歸因於特定因子的變異量」與「無法解釋的變異量」(即殘差)。

若只對「治療」進行單因子變異數分析，因而忽略了「藥物」的效果，那麼分析模型便會將所有由藥物引起的變異量，全都歸入殘差之中！這會使得資料看起來比實際上含有更多的雜訊，導致在二因子變異數分析中被正確判定為顯著的治療效果，在此變得不再顯著。當我們試圖評估某個變項 (如「治療」) 的貢獻時，若忽略了另一個確實有影響力的變項 (如「藥物」)，分析結果便會失真。

當然，忽略那些與研究主題真正無關的變項是完全沒問題的。例如，假設我們記錄了牆壁顏色，並在一個三因子變異數分析中發現它是不顯著的因子，那麼將其忽略，並只報告不含此無關因子的、更簡潔的二因子變異數分析，是完全可以接受的。真正不該做的，是捨棄那些確實有影響力的變項！

14.1.6 解讀多因子變異數分析的結果

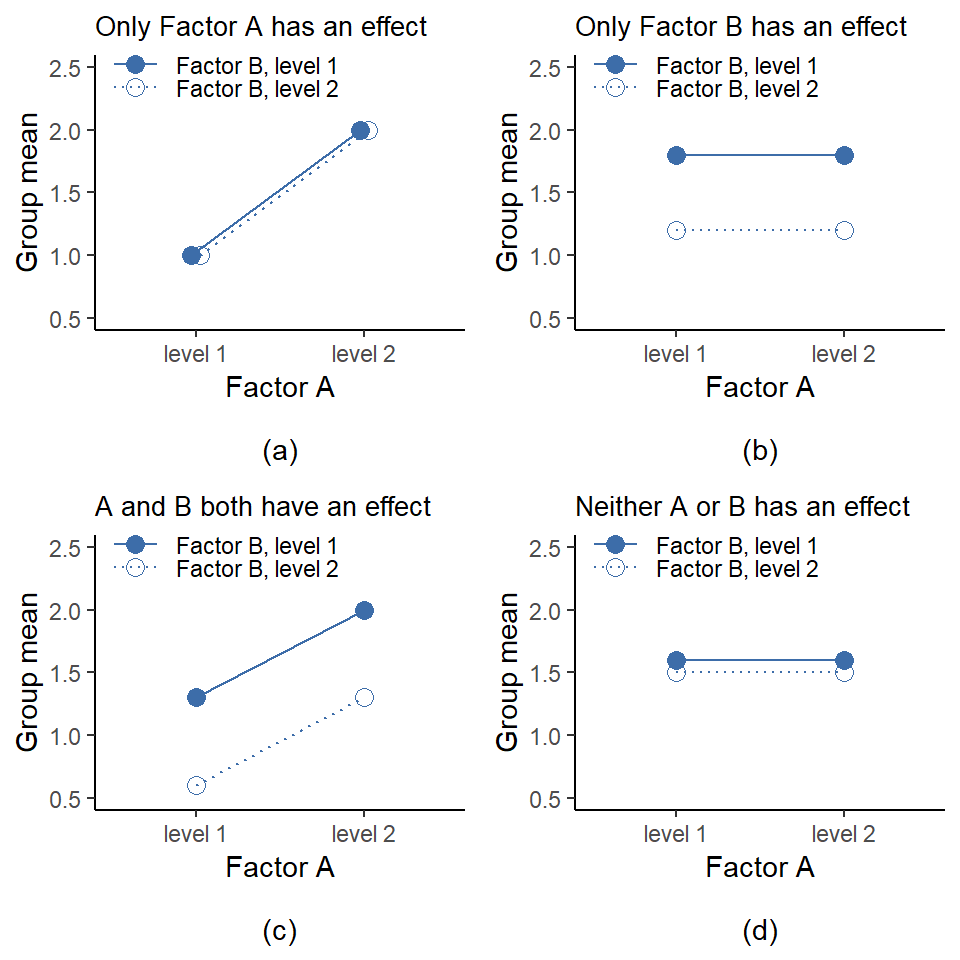
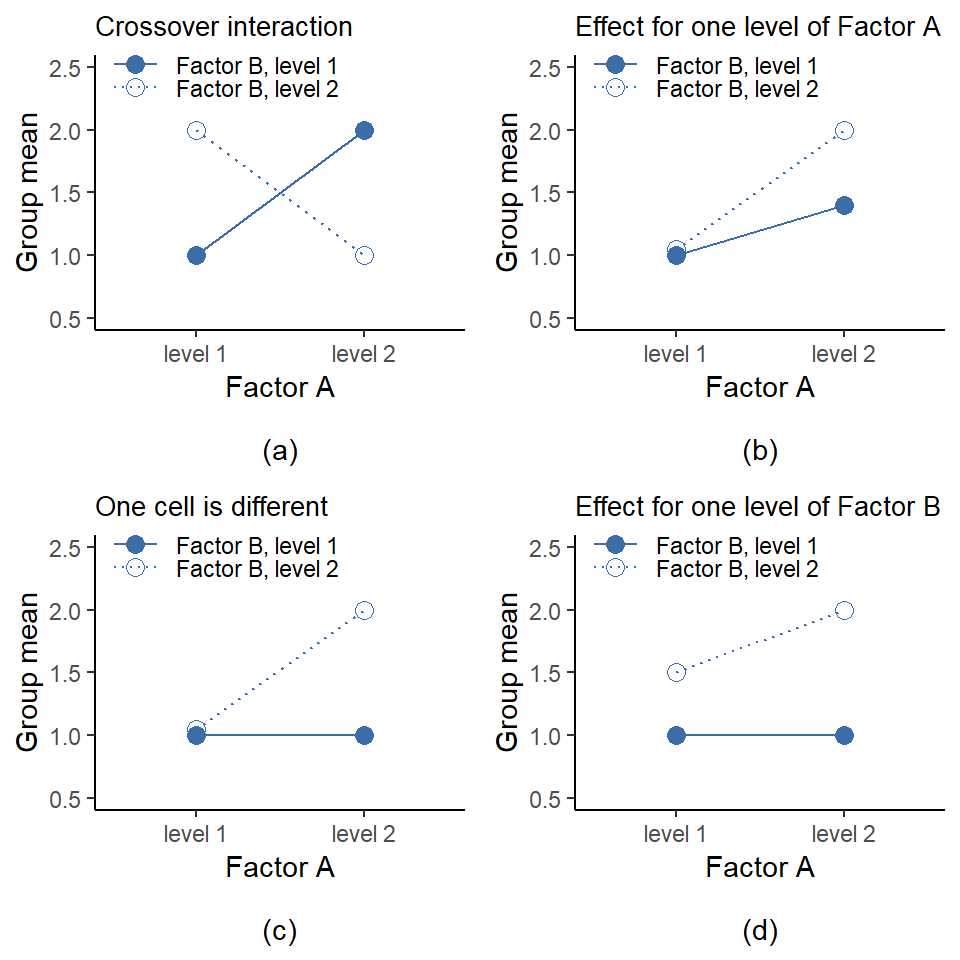
迄今為止我們討論的變異數分析模型涵蓋了我們可能在數據中觀察到的各種不同模式。例如，在兩因素變異數分析設計中有四種可能性：（a）只有因素A有意義，（b）只有因素B有意義，（c）A和B都有意義，（d）A和B都無意義。 ?fig-fig13-4中繪製了這四種可能性的示例。

到目前為止，我們所討論的變異數分析模型，已涵蓋了在資料中可能觀察到的數種不同模式。例如，在一個二因子變異數分析設計中，會出現四種可能的結果：(a) 只有因子 A 具顯著效果；(b) 只有因子 B 具顯著效果；(c) 因子 A 與 B 皆具顯著效果；以及 (d) 因子 A 與 B 皆不具顯著效果。 圖 14.4 是這四種可能性的示意統計圖。

圖 14.4: 沒有交互作用的\(2 \times 2\)因子設計， 四種ANOVA分析可能結果。圖（a）顯示因子A有主要效果，因子B沒有主要效果。圖（b）顯示因子B有主要效果，因子A沒有主要效果。圖（c）顯示因子A和因子B都有主要效果。最後，圖（d）顯示兩個因子都沒有效果。

14.2 平衡且有交互作用的因子設計分析

圖 14.4 所展示的四種資料模式都相當常見，許多資料集都會呈現出這些模式。然而，這並非故事的全貌；到目前為止所介紹的變異數分析模型，依然不足以完整解釋所有組別的平均數表格所代表的意義。為什麼呢？因為我們只能探討「藥物」對情緒的影響，以及「治療」對情緒的影響，卻無法探討兩者之間可能存在的交互作用 (interaction)。

所謂交互作用，是指因子 A 的效果，會隨著因子 B 的處置差別，而產生差異。 圖 14.5 展示在 \(2 \\times 2\) ANOVA 的脈絡下，幾個交互作用效果的範例。在此舉個更具體的例子：假設 Anxifree 與 Joyzepam 這兩種藥物的作用，是由完全不同的生理機制所調節。這可能導致一種情況：無論受試者是否接受CBT治療，Joyzepam 對情緒的效果都差不多；然而，Anxifree 卻是要搭配 CBT 治療時，才會表現出更強的效果。前一節所介紹的 ANOVA 模型，並無法掌握到這樣的概念。

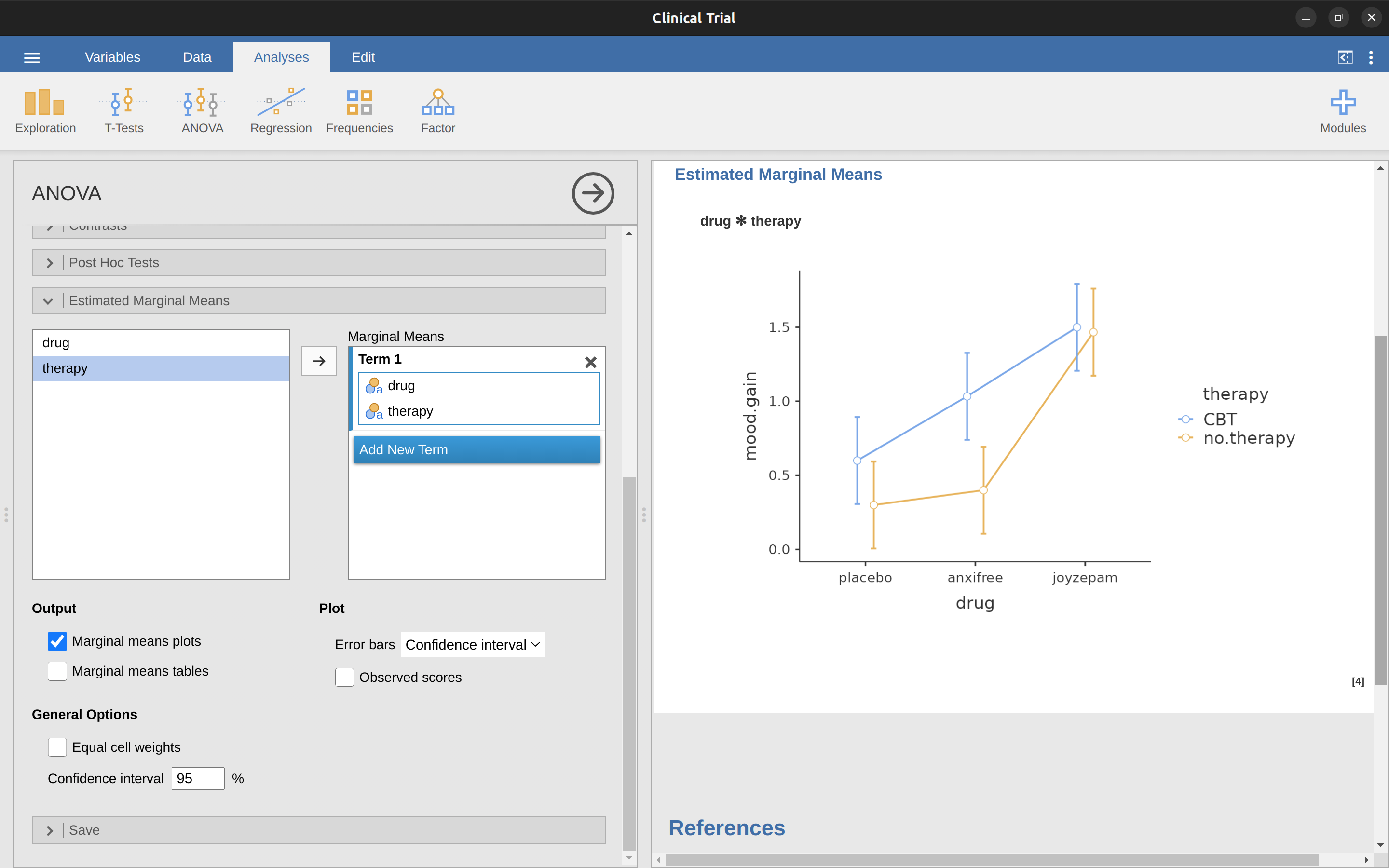
想知道資料中是否真的存在交互作用，一種建議方法是將各組的平均數繪製成圖。我們可以使用 jamovi ANOVA 分析模組設定選項的「估計邊際均值 (Estimated Marginal Means)」來達成 —— 只要將「藥物」與「治療」兩個因子，移動到「第 1 項 (Term 1)」下方的「邊際平均數」欄位，便能得到如 圖 14.6 所示的圖表。我們主要關心的是兩條線不平行的結果。當藥物為 Joyzepam (右側) 時，CBT 的效果 (實線與虛線的差距) 趨近於零，甚至比安慰劑 (左側) 的效果還小。然而，當藥物為 Anxifree (中間) 時，CBT 的效果則明顯大於安慰劑。

究竟這個效果是真實的，還是純粹是機率因素造成的隨機變異？前一節介紹的 ANOVA 模型無法解答這個問題，因為該模型並未考慮交互作用存在的可能性。在這一節，我們學習如何處理這個問題。

圖 14.5: \(2 \times 2\) 因子設計各組數值差異造成的各種交互作用模式

圖 14.6: 設定ANOVA模組選單選項，在報表顯示描繪交互作用折線圖

14.2.1 交互作用的意義？

這一小節要介紹的關鍵概念，便是「交互作用效應」(interaction effect)。至此所討論過的 ANOVA 模型，只有兩個因子 (即「藥物」與「治療」)。然而，一旦加入交互作用，模型便會多出一個成分：「藥物」與「治療」的組合。

直觀來說，交互作用效應的概念相當單純。字面意思是：因子 A 的效果，會隨著因子 B 的不同水平 (或處置) 而有所差異。然而，由範例資料來看，實際上代表什麼意思呢？ 圖 14.5 描繪數種不同的交互作用模式，這些模式雖然彼此差異甚大，卻都是交互作用效應。因此，要將這個模式多變的概念，轉換為統計學家可以運用的數學形式，並非一件全然直接了當的事。

[附加技術細節⁴]

14.2.2 交互作用的自由度

同樣地，計算交互作用的自由度，會比計算主要效果時稍微複雜一些。首先，若考量整個ANOVA模型。要是模型包括交互作用效應，就表示每一個細格都會有其獨特的平均數 (\(\mu_{rc}\))。這代表一個 \(R \times C\) 的因子設計ANOVA模型，便包含了 \(R \times C\) 個所關心的參數，卻只受到一個限制條件約束：所有的細格平均數的平均值，必須等於總平均數。因此，整個模型的自由度為 \((R \times C) - 1\)。然而，因子 A 的主要效果佔了 \(R - 1\) 個自由度，因子 B 的主要效果則佔了 \(C - 1\) 個自由度。這代表交互作用的自由度為：

\[ \begin{aligned} df_{A:B} & = (R \times C - 1) - (R - 1) - (C - 1) \\ & = RC - R - C + 1 \\ & = (R-1)(C-1) \end{aligned} \]

這個結果，正好就是行因子與列因子各自自由度的乘積。

那麼殘差自由度呢？由於模型中新增了會佔用自由度的交互作用項，剩餘的自由度便會減少。具體來說，當模型允許每個細格都有獨特的平均數時，總共有 \(R \times C\) 個組別。若觀測值總數為 \(N_{total}\)，那麼殘差自由度便是觀測值總數減去組別總數，即 \(N_{total} - (R \times C)\)。

14.2.3 使用jamovi完成多因子變異數分析

在 jamovi 中，將交互作用項加入 ANOVA 模型是相當直接了當的。其實這這種設定不僅簡單，更是 ANOVA 分析的預設選項。也就是使用者設定要分析兩因子 ANOVA 時(例如「藥物」與「治療」)，交互作用項 (藥物\(\times\)治療) 就會自動加入模型中⁵。只要模型包括交互作用項並執行完成，就會得到如 圖 14.7 所示的結果。

圖 14.7: 包括藥物\(\times\)治療方法交互作用項的完整ANOVA結果報表

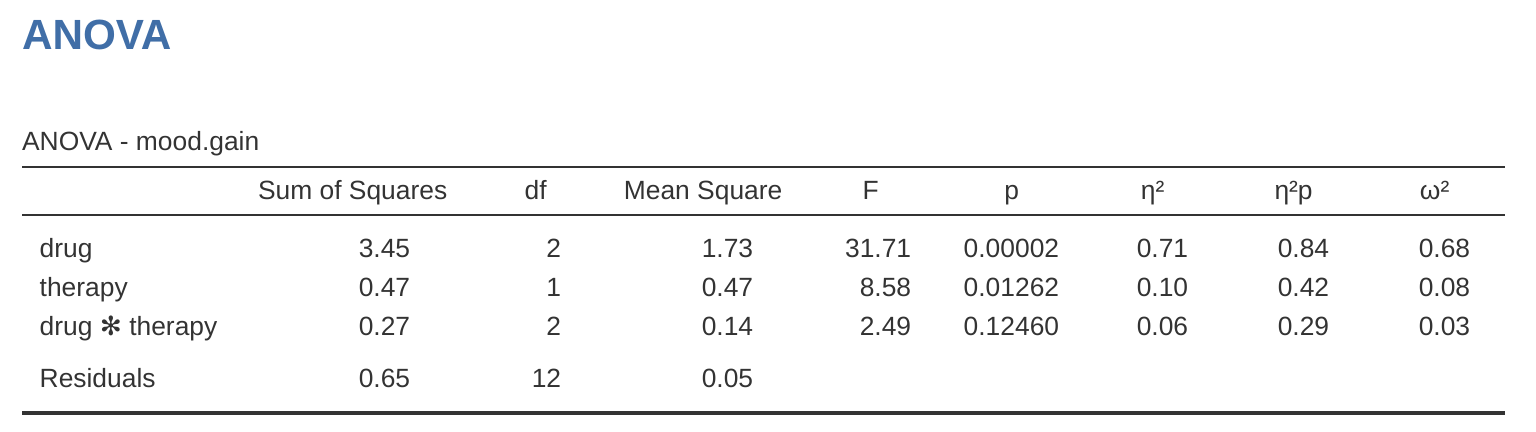
結果顯示，「藥物」種類(\(F(2,12) = 31.7, p < .001\)) 與「治療」方法 (\(F(1,12) = 8.6, p = .013\)) 確實都具有顯著的主要效果，但兩者之間並無顯著的交互作用 (\(F(2,12) = 2.5, p = 0.125\))。

14.2.4 解讀分析結果

在解讀因子設計ANOVA 的結果時，有幾項重點需要考量。首先，它與單因子變異數分析有相同的問題：比如說，即使分析結果顯示「藥物」因子具有顯著的主要效果，我們也無法知道是哪幾種藥物之間彼此存在差異。要找出答案，便需要進行額外的分析。關於這些額外的分析方法，我們將在後續的各種多重比較方案與事後檢定 (Post hoc tests)等小節中討論。這個原則同樣適用於交互作用效果：得知交互作用效果顯著，我們仍無法知道究竟是什麼樣的交互作用造成差異。同樣地，這也需要進行額外的分析。

其次，當分析結果出現顯著的交互作用，但是主要效果不顯著時，會衍生出一個相當特殊的詮釋議題。分析實務時常會發生這種情況，例如 圖 14.5 的圖(a)展示的交叉型交互作用，便是一個典型範例。這個範例的兩個主要效果皆不顯著，但是交互作用效果卻是顯著的。

這種情況不容易解釋，也常讓研究者感到困惑。統計學家給的通用建議是：交互作用顯著時，就不必過度關心主要效果。之所以如此建議，是因為儘管從數學上來說，主要效果的檢定依然完全有效，但在交互作用顯著的前提下，主要效果所檢定的，通常已經不再是個有意義的假說。

回顧 小單元 14.1.1 ，可知主要效果的虛無假說，是檢定各邊際平均數是否相等。然而，邊際平均數便是數個不同細格平均數的平均值。交互作用顯著的意義，便是這些構成邊際平均數的細格平均數，本質上是異質的 (non-homogeneous)。此，再去探討這些異質組別平均值 (即邊際平均數) 之間的差異，其意義何在，就變得不那麼顯而易見了。

以下透過一項虛構的臨床研究來說明。假設我們規劃 2×2 的實驗設計，來比較兩種不同的恐懼症治療方法 (例如系統減敏法 vs. 洪水療法)，以及兩種不同的抗焦慮藥物的效果 (例如 Anxifree vs. Joyzepam)。假如研究發現：使用系統減敏法時，Anxifree 沒有效果；使用洪水療法時，Joyzepam 沒有效果。也就是說，一種藥物只在搭配特定療法時，才會出現效果。

這便是一個典型的交叉型交互作用；用 ANOVA 分析資料便會發現沒有藥物的主要效果，但是交互作用卻是顯著的。那麼，所謂「沒有主要效果」究竟是什麼意思？這意味著，若我們將兩種不同治療方法的效果加以平均，會發現 Anxifree 與 Joyzepam 的平均效果是相同的。

然而，有誰會在意這個平均值呢？沒有任何接受恐懼症治療的病患，所接受的洪水療法與系統減敏法是「平均後」的，這樣解讀不合理。病患接受的只會是其中一種療法。對於某一種療法，某一種藥物是有效的；對於另一種療法，另一種藥物才有效。在這種情況下，交互作用才是重點，主要效果則顯得無關緊要了。

這種情況相當常見。主要效果檢定的對象是邊際平均數，然而當交互作用存在時，研究者往往對邊際平均數比較沒興趣，因為交互作用的存在，恰恰就說明了那些用來計算邊際平均數的細格，其實不應該被混合在一起平均！

當然，這並非意謂著只要交互作用存在，主要效果就必然毫無意義。統計實務常會遇到一種情況：一個顯著的主要效果，伴隨著一個相對微弱但依然顯著的交互作用。因為藥物的主要效果很強，在此情況下，研究者依然可以做出「整體來說，藥物 A 比藥物 B更有效」的結論，不過必須加上一個但書：「這種效果的差異，會因心理治療方式的不同而有所變化」。

總而言之，本節的重點是：每當分析結果出現顯著的交互作用時，都應該停下來，審慎思考主要效果在此脈絡下的真實意義。切勿理所當然地認為主要效果依然是我們所關心的重點。

14.3 變異數分析的效果量

因子設計ANOVA 的效果量計算，與單因子變異數分析所用的方法相當類似 (見 [效果量] 一節)。具體來說，我們同樣可以使用\(\eta^2\) (eta-squared)，來簡易地衡量模型中任一個特定項 (term)** 的整體效果有多大。如同先前所定義，\(\eta^2\) 的計算方式，是將該項的平方和除以總平方和。舉例來說，要計算因子 A 主要效果的公式是：

\[\eta_A^2=\frac{SS_A}{SS_T}\]

如同先前所述，這個數值的詮釋方式與迴歸分析中的 \(R^2\) 非常類似。⁶ 它代表的是結果變項的總變異量中，可由因子 A 的主要效果所解釋的百分比。因此，\(\eta^2\) 的值域介於 0 (完全沒效果) 到 1 (解釋結果變項的全部變異) 之間。此外，模型中所有項的 \(\eta^2\) 值總和，會等於該 ANOVA 模型的總 \(R^2\) 值。舉例來說，若 ANOVA 模型能完美配適資料 (亦即完全沒有組內變異)，則各項 \(\eta^2\) 值的總和將會是 1。當然，這種情況在統計實務極為罕見。

然而，在進行因子設計ANOVA 時，還有第二種研究者們偏好報告的效果量指標，稱為partial \(\eta^2\)。partial \(\eta^2\) (有時也記為 \(p^{\eta^2}\) 或 \(\eta_p^2\)) 的運算概念是：在衡量模型中某一特定項 (例如因子 A 的主要效果) 的效果量時，要刻意忽略模型中其他項的效果 (例如因子 B 的主要效果)。也就是說，要假定所有特定項的效果量皆為零，再來計算此時的 \(\eta^2\) 值會是多少。

partial \(\eta^2\)的計算相當簡單，只要從分母中，移除其他項所對應的平方和即可。換言之，若想計算因子 A 主要效果的partial \(\eta^2\)，其分母就只會是因子 A 的平方和與殘差平方和的總和。

\[\text{partial }\eta_A^2= \frac{SS_A}{SS_A+SS_R}\]

這個值永遠會比 \(\eta^2\) 來得大，我內心的犬儒主義者懷疑這正是partial \(\eta^2\) 之所以受歡迎的原因。同樣地，這個數值的範圍也介於 0 (沒有效果) 到 1 之間。

然而，要詮釋一個較大的partial \(\eta^2\) 值代表何種意義，就有些棘手了。特別需要注意的是，不同特定項之間的partial \(\eta^2\) 值是不能直接相互比較的！舉例來說，假設完全沒有組內變異量，亦即 \(SS_R = 0\)。這代表模型中每一個項的partial \(\eta^2\) 值都會是 1。但這不代表模型中所有特定項都同等重要，或其效果大小完全相同。它只代表模型中每一個特定項的效果量，相對於殘差變異量都很大，但無法用來比較不同項之間何者更重要。

透過一個具體範例，可以更容易理解箇中差異。首先，我們來檢視 圖 14.3 ，一開始示範的不含交互作用項 ANOVA 模型，各項效果量數值列在 表 14.6 。

表 14.6:

無交互作用項目的ANOVA模型的效果量

	eta.sq	partial.eta.sq
drug	0.71	0.79
therapy	0.10	0.34

首先看各特定項的 \(\eta^2\) 值，「藥物」因子能解釋「情緒改善程度 (mood.gain)」 71% 的變異量 (\(\eta^2 = 0.71\))，而「治療」因子僅解釋了 10%。剩餘 19% 的變異量則無法被解釋 (亦即殘差佔了結果變項總變異量的 19%)。整體而言，這代表「藥物」具有非常大的效果[^factorial-anova-7]，而「治療」的效果則屬中等。

[^factorial-anova-7]：我會認為這個效果量大到有點不切實際。這份資料集的人造痕跡在這裡可說是展露無遺了！

接著來看各特定項的partial \(\eta^2\) (請見 圖 14.3 )。由於「治療」的效果並不算特別大，因此在計算時將其效果加以控制，並不會造成太大改變，這使得「藥物」的partial \(\eta^2\) 僅微幅上升至 \(\eta_p^2 = 0.79\)。反之，由於「藥物」的效果非常強，控制此效果便會造成顯著的差異；因此，當我們計算「治療」的partial \(\eta^2\) 值時，會發現它大幅上升至 \(\eta_p^2 = 0.34\)。

這裡必須探討的問題是：這些partial \(\eta^2\) 值究竟代表什麼意義？詮釋因子 A 主要效果的partial \(\eta^2\) 值，一種常見的方式是，將其視為一個「假設性實驗」的結果，在該實驗中，僅有因子 A 是唯一的變項。也就是說，雖然在我們當前的實驗中，因子 A 與 B 都是變項，但我們可以想像另一個只變動因子 A 的實驗；而partial \(\eta^2\) 這個統計量所代表的，便是在那個假設性實驗中，我們預期因子 A 能解釋結果變項多少百分比的變異量。然而，必須注意的是，這種詮釋方式 (如同許多與主要效果相關的概念)，在模型存在一個巨大且顯著的交互作用時，將會變得不太有意義。

接著來看交互作用效果，表 14.7 呈現有交互作用項的模型 (請見 圖 14.7 )，效果量的計算結果。可以看到，主要效果的 \(\eta^2\) 並未改變，但是partial \(\eta^2\) 不一樣了：

表 14.7:

有交互作用項目的ANOVA模型的效果量

	eta.sq	partial.eta.sq
drug	0.71	0.84
therapy	0.10	0.42
drug*therapy	0.06	0.29

14.3.1 估計細格平均數

在許多實務情況，研究者會希望根據 ANOVA 的結果，報告所有細格平均數的估計值，以及其對應的信賴區間 (confidence intervals)。在 jamovi 中，可使用 ANOVA 分析裡的「估計邊際平均數」選項來達成此目的，如 圖 14.8 的示範。若所執行的 ANOVA 是一個飽和模型 (saturated model)，也就是模型包含所有可能的主要效果與交互作用效果項目，那麼細格平均數的估計值，實際上會與樣本平均數完全相同；不過，細格平均數的信賴區間將使用標準誤的共同估計值 (pooled estimate)計算，而非各組各自獨立估計。

圖 14.8: jamovi報表區展示飽和模型的各組邊際平均值，列出臨床試驗資料集構成交互作用項目的各細格估計值

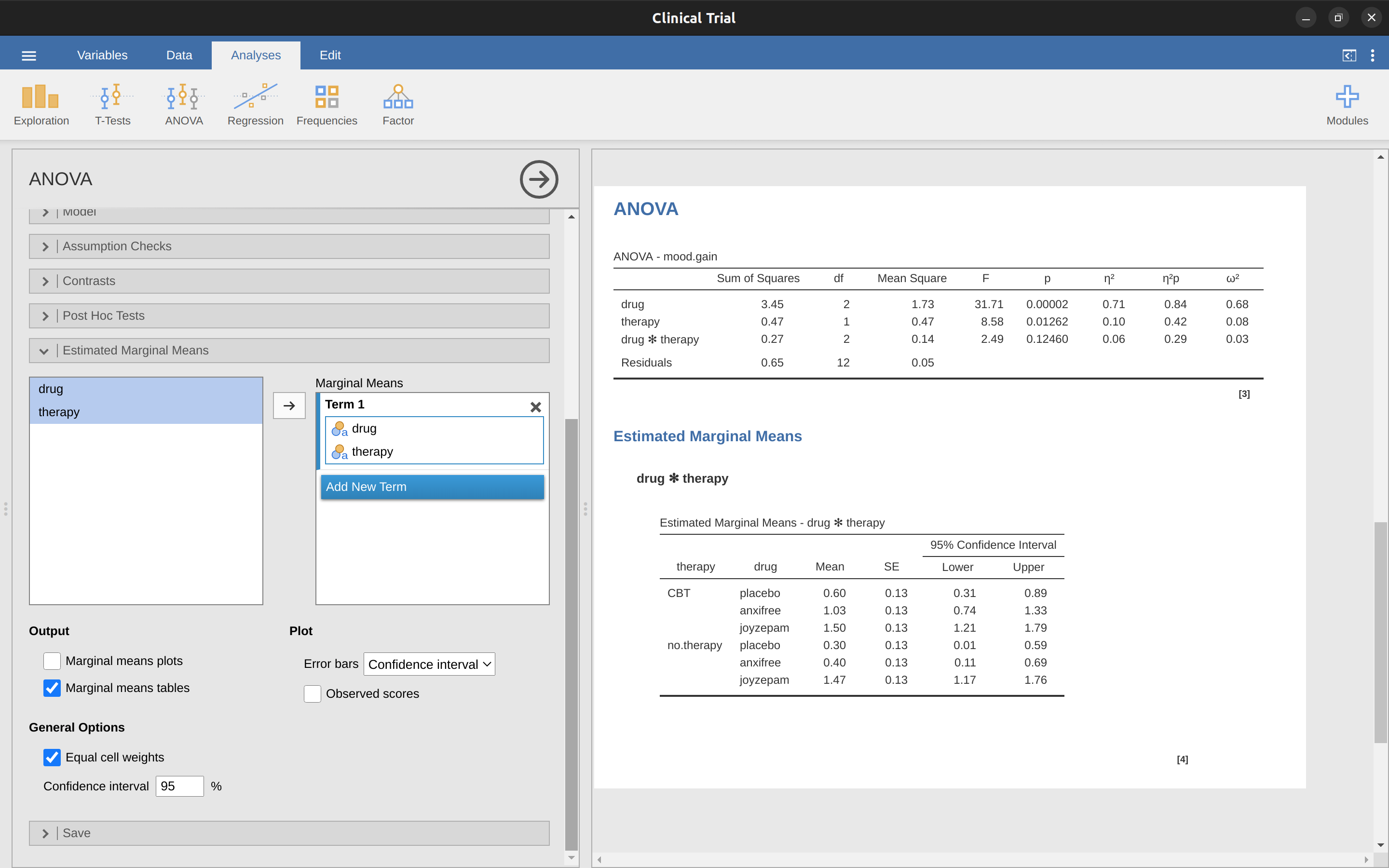
從輸出結果中可以看到，「無治療」條件的「安慰劑」組，估計情緒改善程度平均值為 \(0.300\)，95% 信賴區間為 \(0.006\) 至 \(0.594\)。需要注意的是，這些信賴區間估計值，與各組獨立計算的信賴區間並不相同。這是因為 ANOVA 模型假定這份資料符合變異數同質性 (homogeneity of variance)，因此使用標準差的共同估計值。

當使用非飽和模型 (亦即不含交互作用項的模型) 時，所估計的細格平均數將會與樣本平均數不同。此時，jamovi 不會回報樣本平均數，而是會基於邊際平均數 (亦即假定不存在交互作用) 來計算預期的細格平均數。

套用我們先前建立的符號系統，此時所回報的細格平均數 (\(\mu_{rc}\)，即因子 A 第 r 個水平與因子 B 第 c 個水平的平均數)，其計算方式會是 \(\mu_{..} + \alpha_r + \beta_c\)。若兩個因子之間確實不存在交互作用，這個估計值其實會比原始的樣本平均數，能更準確地估計母群平均數。

在 jamovi 的 ANOVA 分析模組，可透過「模型 (Model)」設定選項來移除交互作用項，得到 圖 14.9 的示範分析結果。

圖 14.9: jamovi報表區展示非飽和模型的各組邊際平均值，列出臨床試驗資料集構成交互作用項目的各細格估計值

14.4 檢核變異數分析的適用條件

與單因子變異數分析一樣，因子設計因子變異數分析也有幾項關鍵的適用條件，即變異數同質性 (homogeneity of variance，所有組別的標準差皆相同)、殘差的常態性 (normality of the residuals)，以及觀測值的獨立性 (independence of the observations)。前兩項是可以透過統計方法來檢核的，第三項則需要研究者根據研究設計自行評估，判斷不同觀測值之間是否存在特殊關聯。以獨變項是「時間」的重複測量(repeated measures)設計來說，時間點一與時間點二的觀察值是有相關的，因為都是來自同一位參與者。此外，若研究者不是使用飽和模型 (像是省略交互作用)，等於也接受「被省略的項目是不重要的」的假設。當然，這一點可以很容易地透過「執行包含該省略項的 ANOVA 模型，並檢視其是否顯著」來進行確認。那麼，該如何檢核變異數同質性與殘差的常態性呢？事實上，檢核方法相當簡單，與單因子變異數分析的做法並無不同。

14.4.1 變異數的同質性

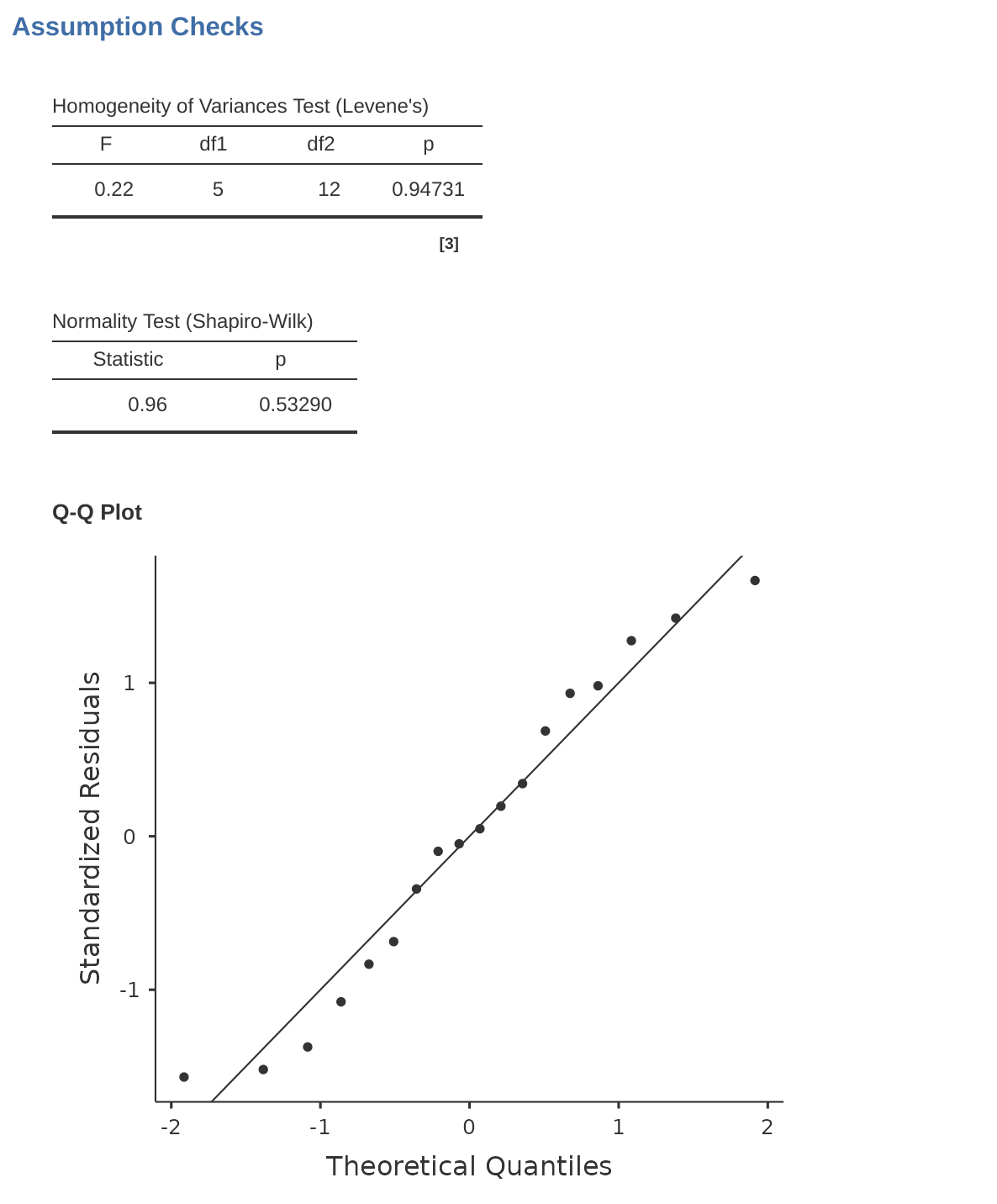
如同 小單元 13.6.1 所述，一個好的做法是，先建立視覺化圖表來檢視，比較各組別或各類別的標準差，然後再看 Levene 檢定的結果是否與圖表一致。Levene 檢定的理論基礎已在 小單元 13.6.1 介紹過，此處不再贅述。Levene檢定預設統計實務是採用飽和模型 (包含所有特定項的模型)，因為檢定的主要目標是組內變異數，而這個數值只有在飽和模型下進行計算才最具意義。在 jamovi 中，可在 ANOVA 分析的「適用條件檢核 (Assumption Checks)」–「同質性檢定 (Homogeneity Tests)」選項中執行 Levene 檢定，示範結果可參考 圖 14.10 。若 Levene 檢定結果不顯著，而且與標準差的視覺化趨勢一致，我們便可以認定變異數同質性的適用條件並未被違反。

14.4.2 殘差的常態性

與單因子變異數分析一樣，我們可以用 小單元 13.6.4 介紹過的方法測試殘差的常態性。不過，通常最好的方法是先使用QQ圖檢查有沒有殘差太大的資料。請參見 圖 14.10 的示範。

圖 14.10: ANOVA模型的適用條件檢定

14.5 共變數分析 (ANCOVA)

變異數分析的一種變形適合用於當研究中包含一個可能與依變項有相關的額外連續變項時。這個額外的變項，通常稱為共變項 (covariate)。 將共變項加入分析之中的做法，便稱為共變異數分析 (analysis of covariance, ANCOVA)。

執行共變異數分析之前，通常會根據共變項的影響程度「校正 」(adjusted) 依變項的數值。接著依照變異數分析的流程，檢定各組之間「校正後」的平均數是否存在差異。這種校正能提升分析的精確度，因此在檢定依變項的組間平均數是否相等時，能提供更強的檢定力 (power)。共變異數分析是如何提升檢定力的呢？雖然通常共變項並非研究所關心的重點，但是透過統計方法控制共變項，可以降低實驗誤差的估計值；藉由減少誤差變異數，就能提升統計結果的精確度。也就是說，研究者不當地「未能拒絕」虛無假說 (即偽陰性，或稱型二錯誤 Type II error) 的機率將會降低。也就是說，研究者錯將結果認定為不可拒絕虛無假說 (偽陰性，或稱型二錯誤 (Type II error)) 的機率將會降低。

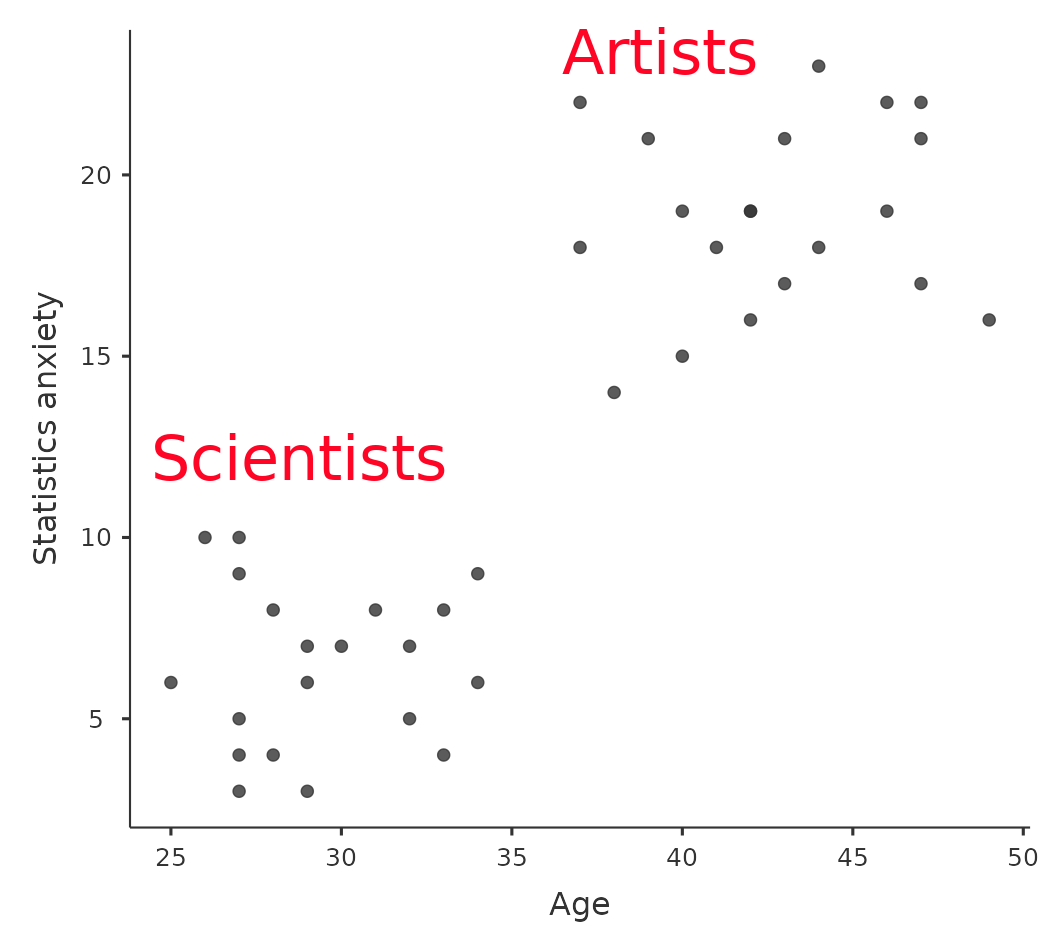
儘管有前述優點，共變異數分析仍然存在一個缺陷，可能會抵銷真實存在的組間差異，使用者必須避免這種狀況。以 圖 14.11 舉例說明，這份散佈圖呈現「統計焦慮」與「年齡」的關係，同時顯示兩個背景或偏好相異的分組：文組學生(Artists)與理組學生(Scientists)。

若將這個例子的年齡當作共變項，共變異數分析的結果可能會得出「兩組學生的統計焦慮程度並無差異」的結論。這個結論合理嗎？很可能不合理。因為看了散佈圖可知，兩組的年齡分佈並未重疊，因此變異數分析實質上是「從沒有資料存在的空間推斷研究結果」( Everitt (1996), p. 68 )。

圖 14.11: 統計焦慮與年齡的圖示，對於兩個不同的組別

顯然，要用共變異數分析處理組別差異懸殊的資料時，必須格外謹慎。這個原則無論是在單因子還是因子設計中都適用，因為共變異數分析可以應用於這兩種研究設計。

14.5.1 使用jamovi完成共變數分析

一位健康心理學家想探討平常通勤方式與壓力感受對幸福感的影響，參與者的年齡當作共變項。完整的研究資料集可見 ancova.csv 。

用 jamovi 開啟檔案後，執行共變數分析的步驟是：點選「分析 (Analyses)」–「變異數分析 (ANOVA)」–「共變異數分析 (ANCOVA)」，開啟分析對話窗 (參考 圖 14.12 )。將依變項「happiness」放進「依變項 (Dependent Variable)」欄位；將自變項「stress」與「commute」放進「固定因子 (Fixed Factors)」欄位；最後將共變項「age」放進「共變項 (Covariates)」欄位。接著，開啟選單「估計邊際平均數 (Estimated Marginal Means)」，設定圖表與表格選項。

圖 14.12: jamovi 共變異數分析 (ANCOVA) 操作選單

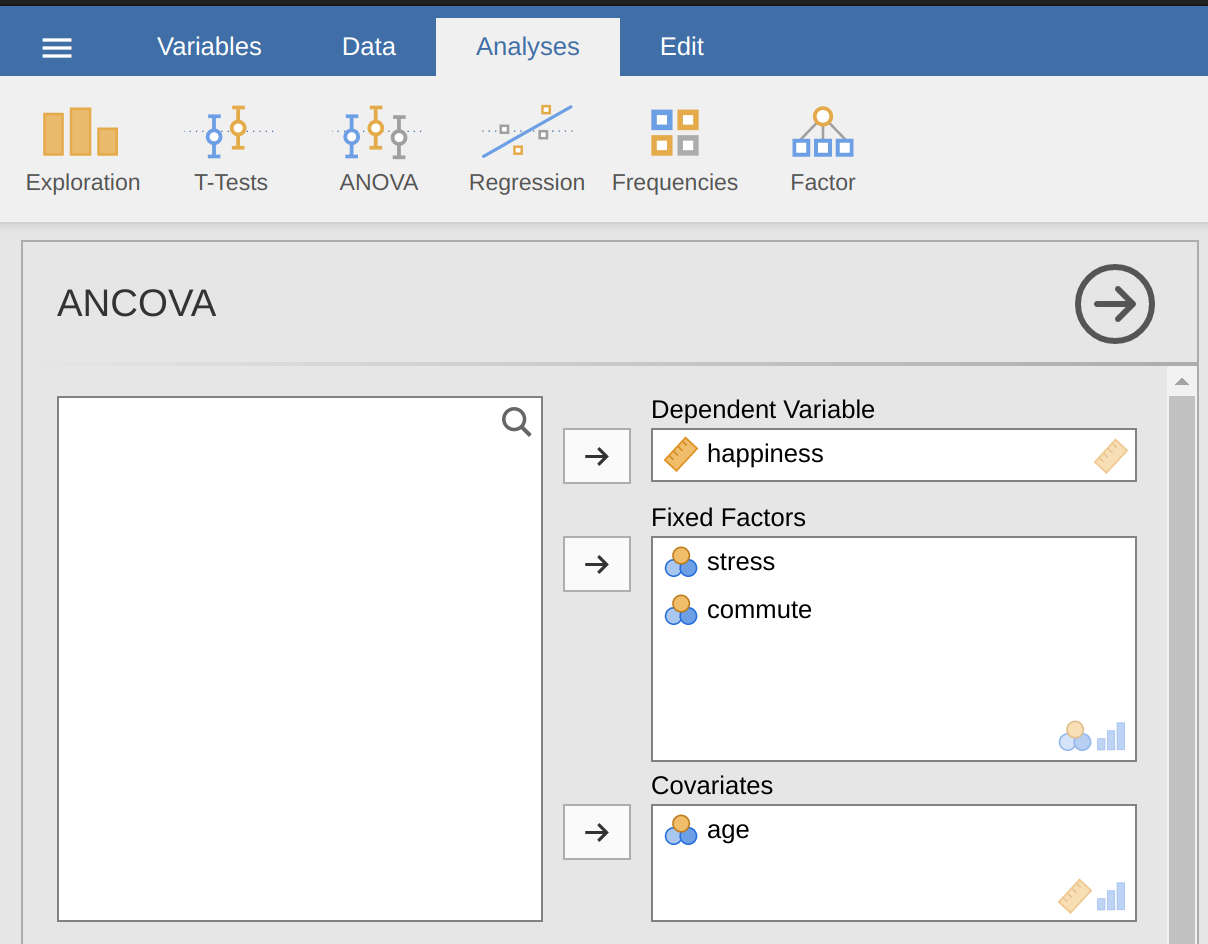
jamovi 的報表區會輸出 ANCOVA 結果表，標題是「受試者間效應檢定 (Tests of Between-Subjects Effects)」(參考 圖 14.13 )。首先看到共變項「age」的 F 值達到顯著水準 (\(p = .023\))，這代表年齡是依變項「happiness」的一個重要預測變項。接著檢視估計邊際平均數 (參考 圖 14.14 )，因為模型包含共變項「age」，會發現其數值已經過校正 (此處數值與未包含共變項的分析結果會有所不同)。運用像 圖 14.15 的視覺化圖表，更能詮釋顯著效果的意義。

圖 14.13: jamovi 共變異數分析 (ANCOVA) 結果表格：以「壓力」與「通勤方式」為因子，「年齡」為共變項，「幸福感」為依變項的分析結果

圖 14.14: 「壓力」與「通勤方式」對「幸福感」的平均數表格 (已針對共變項「年齡」進行校正)，含 95% 信賴區間

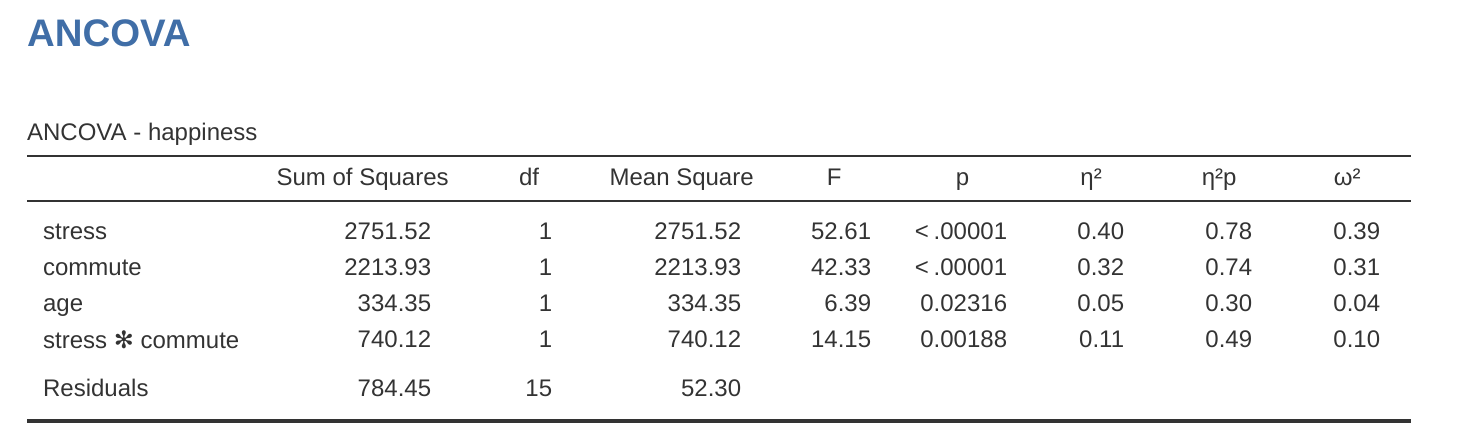
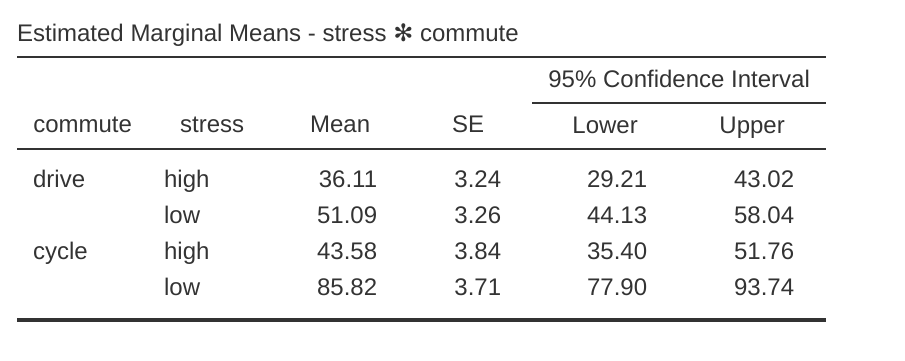
從表格中可見，「壓力」主要效果的 F 值為 52.61，對應的 p 值小於 .001；「通勤方式」主要效果的 F 值為 42.33，p 值亦小於 .001。由於這兩個 p 值都小於一般判定的顯著水準 (\(p < .05\))，我們可以宣稱「壓力」(\(F(1, 15) = 52.61, p < .001\)) 與「通勤方式」(\(F(1, 15) = 42.33, p < .001\)) 皆有顯著的主要效果。此外，研究也發現兩者之間有顯著的交互作用 (\(F(1, 15) = 14.15, p = .002\))。

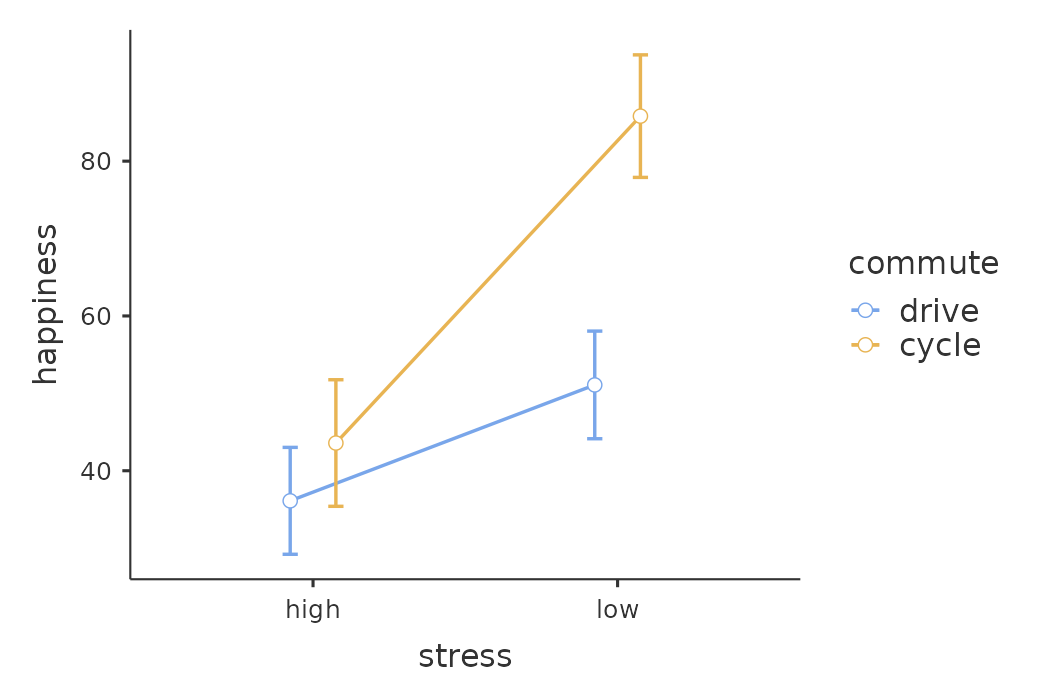
我們可以從 圖 14.15 看到，將年齡作為共變項加入 ANCOVA 模型後，校正後的邊際平均幸福感分數。這個交互作用的模式可以從 圖 14.15 的圖表中看出：低壓力且騎單車上班的分組，幸福感顯著高於其他三組，包括低壓力/開車上班，以及高壓力的所有通勤方式分組。分析結果同時也顯示顯著的「壓力」主要效果 (低壓力者比較高壓力者幸福)，以及顯著的「通勤方式」主要效果 (平均來說，騎單車者比開車者幸福)。

圖 14.15: 「壓力」與「通勤方式」對「幸福感」的平均數交互作用圖

還有一點需要注意，若想將共變項加入 ANOVA 模型，必須符合一項額外的適用條件：共變項與依變項之間的關係，在自變項的每一個水平之間都應當是相似的。要檢核這項條件，可以操作在 jamovi 的「模型 (Model)」–「模型項 (Model terms)」選單，為共變項與每一個自變項都新增交互作用項，來進行檢核。若每項交互作用效果不顯著，便可以移除；反之，若交互作用顯著，則可能需要採用更進階的其他統計方法(這部分已經超出本書範圍，建議讀者諮詢友善的統計學家)。

14.6 變異數分析就是線性模型

關於變異數分析與迴歸分析，有一件極為重要的事需要知道，就是去理解它們的本質是相同的。從表面上看，讀者可能不這麼認為。畢竟，本書至今的描述，似乎都在暗示變異數分析主要用途是檢定組間差異，而迴歸則是用來處理變項之間的相關性。就此而言，這樣的說法完全正確。然而，深入探究便會發現，變異數分析與迴歸的底層機制 (underlying mechanics) 極為相似。事實上，讀者若仔細回想，應該已經看見許多蛛絲馬跡：兩者都需要計算差異平方和 (SS)、都是使用 F 檢定等等。回想起來，實在很難擺脫 單元 12 與 單元 13 的內容有些重複的感覺。

之所以如此，是因為變異數分析與迴歸都是一種線性模型 (linear models)。對迴歸分析而言，這點無庸置疑。我們用來定義預測變項與結果變項之間關係的迴歸方程式，本身就是一個直線方程式，因此它顯然是一個線性模型，寫出來的公式是：

\[Y_p=b_0+b_1 X_{1p} +b_2 X_{2p} + \epsilon_p\]

其中 \(Y_p\) 代表第 p 個觀測值 (例如第 p 位受試者) 的結果變項數值；\(X_{1p}\) 是該觀測值的第一個預測變項數值；\(X_{2p}\) 則是第二個預測變項數值；\(b_0\)、\(b_1\) 與 \(b_2\) 是迴歸係數；而 \(\epsilon_p\) 則是第 p 個殘差。若我們先忽略殘差 \(\epsilon_p\)，只關注迴歸線，便會得到以下公式：

\[\hat{Y}_p=b_0+b_1 X_{1p} +b_2 X_{2p}\]

其中 \(\hat{Y}_p\) 是迴歸線對第 p 位受試者的 Y 預測值，對應實際觀測到的 \(Y_p\)。然而，先前章節較未闡明的是，我們也可以將變異數分析寫成線性模型的形式。其實這麼做能更直接了解變異數分析的本質。接下來，本書將從一個非常簡單的例子開始，將一個 \(2 \times 2\) 的因子設計ANOVA 改寫為線性模型。

14.6.1 示範資料

為了讓說明更具體，假設我們的結果變項，是學生課堂的成績，這是一個比率量尺 (ratio-scale) 變項，分數範圍介於 0% 到 100% 之間。研究中有兩個感興趣的預測變項：學生是否有出席上課 (變項 attend)，以及學生是否有讀過指定教材 (變項 reading)。我們將這兩個變項編碼：若學生有上課， attend = 1，反之則為 0。同樣地，若學生有讀過指定教材，則 reading = 1，反之則為 0。

好了，到目前為止還算簡單。接下來需要讀者辛苦一點，我要開始用一些數學符號說明了。在這個範例中，我們以 \(Y_p\) 代表班上第 p 位學生的成績。這個符號標示與本章先前的用法不完全相同。先前我們使用 \(Y_{rci}\) 來代表在預測因子 1 (列因子) 的第 r 組、且在預測因子 2 (行因子) 的第 c 組中的第 i 位受試者。那套符號標示在描述如何計算差異平方和 (SS) 時非常方便，但用在這個範例卻顯得礙手礙腳，因此接下來將更新符號標示。

\(Y_p\) 在視覺上比 \(Y_{rci}\) 感覺更簡潔，但缺點是無法追蹤受試者的組別歸屬資訊 (group memberships)。也就是說，若讀者看到 \(Y_{0,0,3} = 35\)，便能立刻知道我們所指的是第三位缺課 (attend = 0) 又未讀指定教材 (reading = 0) 的學生，而他的成績是 35 分。但若只寫 \(Y_p = 35\)，我們只能知道第 p 位學生的成績不好，卻沒有寫出關鍵的組別資訊。當然，要解決這個障礙並不難。我們只需引入兩個新的變項 \(X_{1p}\) 與 \(X_{2p}\) 來記錄這些資訊即可。以這個示範的學生案例來說，我們已經知道 \(X_{1p} = 0\) (attend = 0)，而且 \(X_{2p} = 0\) (reading = 0)。如此一來，資料便會呈現如同 表 14.8 的樣貌。

表 14.8:

成績、出席、與教材閱讀狀態資料表

person, \(p\)	grade, \(Y_p\)	attendance, \(X_{1p}\)	reading, \(X_{2p}\)
1	90	1	1
2	87	1	1
3	75	0	1
4	60	1	0
5	35	0	0
6	50	0	0
7	65	1	0
8	70	0	1

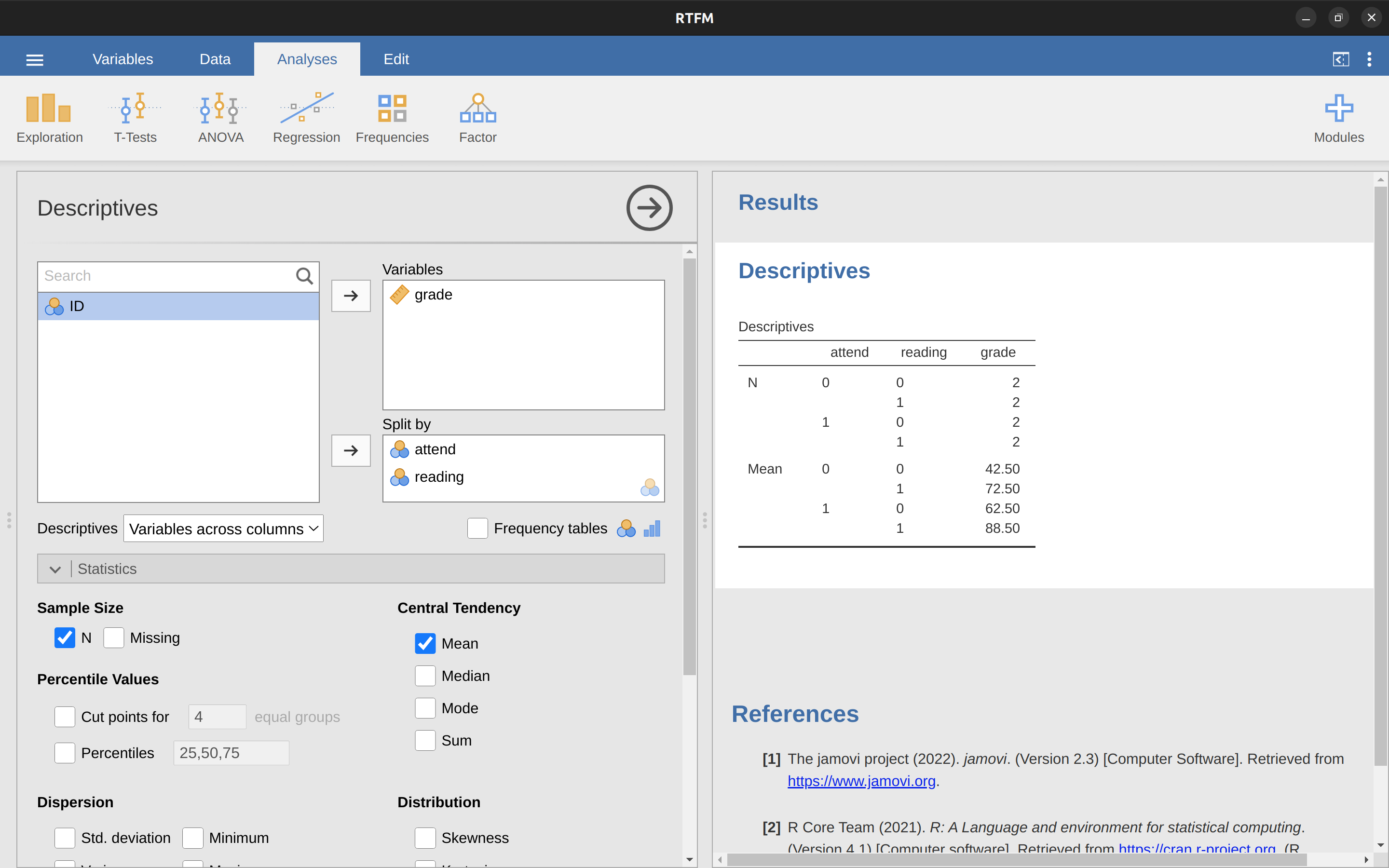
當然，這沒什麼特別之處，這正是我們所預期的資料格式！(詳見資料檔 rtfm.csv)。我們可以使用 jamovi 的描述統計 (Descriptives)分析，來確認這筆資料集屬於平衡設計，也就是 attend 與 reading 的每種組合裡，都有 2 個觀測值。同樣地，我們也能計算出每種組合的平均成績，如同 圖 14.16 的示範。從這些平均分數來看，可以讓人強烈地感覺到，閱讀指定教材與出席上課兩者都相當重要。

圖 14.16: rtfm 資料集的 jamovi 描述統計結果

14.6.2 以迴歸模型處理非連續因子

好啦，讓我們繼續數學符號的說明。現在起可用三個數值變項來表示資料內容：一個連續變項 \(Y\)，以及兩個二元變項 (binary variables) \(X_1\) 與 \(X_2\)。這裡希望讀者能理解，\(2 \times 2\) 因子設計ANOVA，完全等同於以下的迴歸模型：

\[Y_p=b_0+b_1 X_{1p} + b_2 X_{2p} + \epsilon_p\]

你沒看錯，這與先前用來描述有兩個預測變項的迴歸模型方程式完全相同！唯一的差別是，\(X_1\) 與 \(X_2\) 是二元變項 (數值只能是 0 或 1)，但是在典型的迴歸分析中，我們會先認定 \(X_1\) 與 \(X_2\) 是連續變項。

要如何說服讀者相信兩套方程式是等同的呢？一種可能是進行冗長的數學推導，但本書的多數讀者可能會覺得此舉令人厭煩而且沒幫助。因此，本書將採取另一種方式：先解釋基本概念，再透過 jamovi 來展示變異數分析與迴歸分析不僅相似，本質更是完全相同。讓我們先用變異數分析來執行分析。以下示範使用 rtfm 資料集，jamovi 的分析結果如 圖 14.17 的展示。

圖 14.17: jamovi 對 rtfm.csv 資料集的 ANOVA 分析結果 (已排除交互作用項)

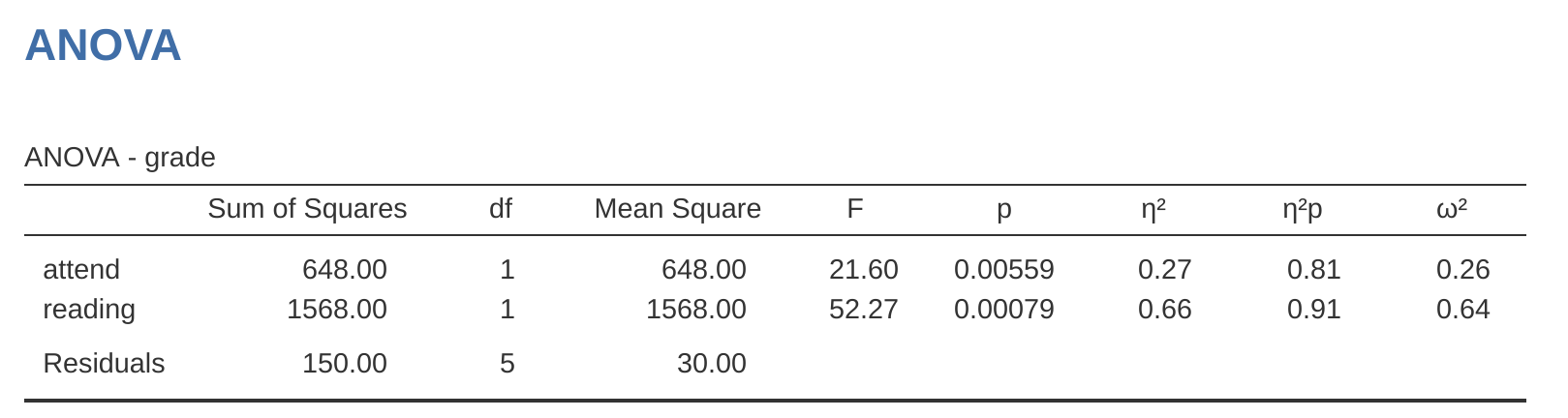
根據 ANOVA 表格及先前呈現的平均分數，可以解讀幾個關鍵結果：學生有出席課程 (\(F_{1,5} = 21.6, p = .0056\)) 以及有閱讀指定教材 (\(F_{1,5} = 52.3, p = .0008\))，會讓成績顯著較高。請各位先記下這些 p 值與 F 統計值。

接著讓我們從線性迴歸的角度來思考如何分析這筆資料，先將 rtfm 資料集的attend 與 reading 編碼為數值預測變項。以迴歸模型來說，這種做法完全可以接受。因為相較於缺課的學生 (attend = 0)，有來上課的學生 (attend = 1) 確實可被視為符合「較多的出席」。因此，將此作為迴歸模型中的預測變項並無不妥。雖然這個預測變項只有兩個數值，和之前的範例相比有些不尋常，但這並未違反任何線性迴歸的適用條件，且結果詮釋也相當直觀。若 attend 的迴歸係數大於 0，代表有出席課程的學生成績較高；若係數小於 0，則代表有出席課程的學生成績反而較低。這個的做法同樣適用 reading 變項。

不過先稍停一下，為什麼這樣的做法是可行的呢？對於修過幾門統計課、對數學不會陌生的讀者來說，這種做法相當直觀；但是對於初學者而言，卻不見得如此。要讓初學者理解其中緣由，仔細檢視幾個特定學生的案例會很有幫助。讓我們用資料集裡的第 6 位與第 7 位學生 (\(p=6\) 與 \(p=7\)) 來解釋。

這兩位學生都沒有課前閱讀指定教材，因此這兩位學生的reading變項都可以設定 reading = 0。用數學符號表示的話，就是 \(X_{2,6} = 0\) 與 \(X_{2,7} = 0\)。不過，第 7 位學生有出席課程 (attend = 1, \(X_{1,7} = 1\))，第 6 位學生則沒有 (attend = 0, \(X_{1,6} = 0\))。接下來，我們來看看將這些數值代入迴歸線公式後會發生什麼事。

迴歸模型預測第 6 位學生的成績為：

\[ \begin{split} \hat{Y}_6 & = b_0 + b_1 X_{1,6} + b_2 X_{2,6} \\ & = b_0 + (b_1 \times 0) + (b_2 \times 0) \\ & = b_0 \end{split} \]

因此，我們預期這位學生的成績會相等於截距項 \(b_0\) 代表的數值。那麼第 7 位學生呢？將數值代入迴歸線公式後，會得到：

\[ \begin{split} \hat{Y}_7 & = b_0 + b_1 X_{1,7} + b_2 X_{2,7} \\ & = b_0 + (b_1 \times 1) + (b_2 \times 0) \\ & = b_0 + b_1 \end{split} \]

因為這位學生有出席課程，預測成績等於截距項 \(b_0\) 加上 attend 變項的係數 \(b_1\)。所以，若 \(b_1\) 大於 0，我們預期有出席課程的學生，成績會高於缺課的學生。若此係數為負，則預期結果相反：有出席課程者的表現反而更差。

其實還可以再拿另一個學生示範。以第 1 位學生來說，他既有出席課程 (\(X_{1,1} = 1\)) 也有先讀指定教材 (\(X_{2,1} = 1\))。將這些數值代入迴歸模型會得到：

\[ \begin{split} \hat{Y}_1 & = b_0 + b_1 X_{1,1} + b_2 X_{2,1} \\ & = b_0 + (b_1 \times 1) + (b_2 \times 1) \\ & = b_0 + b_1 + b_2 \end{split} \]

因此，若我們假定出席課程有助於提升成績 (\(b_1 > 0\))，且閱讀指定教材也有助於提升成績 (\(b_2 > 0\))，那麼迴歸線的預測結果就是：第 1 位學生的成績將會高於第 6 位與第 7 位學生。

至此，讀者大概不會再感到意外：迴歸模型會預測第 3 位學生 (有閱讀、未出席) 的預測成績是 \(b_0 + b_2\)。這裡就不再為讀者做一次示範了，所有學生的預測成績已經整理在 表 14.9 。

表 14.9:

迴歸模型的預測成績

		read textbook
		no	yes
attended?	no	\( \beta_0 \)	\( \beta_0 + \beta_2 \)
	yes	\( \beta_0 + \beta_1 \)	\( \beta_0 + \beta_1 + \beta_2 \)

從表格中可以看到，截距項 \(b_0\) 的作用，就是代表那些既未出席課程、也未閱讀指定教材的學生的基準線成績。同樣地，\(b_1\) 代表預期有出席課程而帶來的成績提升；而\(b_2\) 則代表閱讀指定教材所能帶來的成績提升。若是改用變異數分析的術語來說，我們很自然地把 \(b_1\) 當做「出席」的主要效果，把 \(b_2\) 當做「閱讀」的主要效果。就一個簡單的 \(2 \\times 2\) 變異數分析來說，兩種模型確實是如此對應。

好了，既然我們已經可以接受為何 ANOVA 與迴歸分析本質上是同一回事，就讓我們實際使用 rtfm 資料集與 jamovi 的迴歸分析功能，來做個驗證。用已經學過的方式執行迴歸分析，會得到 圖 14.18 所示範的結果。

圖 14.18: jamovi 對 rtfm.csv 資料集的迴歸分析結果 (已排除交互作用項)

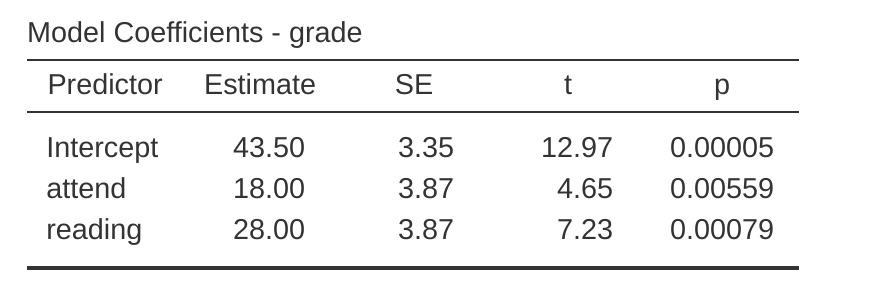
這裡有幾點值得注意。首先，截距項是43.5，這個數值相當接近既未閱讀指定教材也未出席課程的學生成續平均數42.5。還有，我們得到 attend (出席) 變項的迴歸係數 \(b_1 = 18.0\)，這代表有出席課程的學生，成績比未出席者的平均數高 18 分。因此，我們的預期是：那些有出席課程但未閱讀指定教材的學生，成績平均數應該是 \(b_0 + b_1\)，也就是 \(43.5 + 18.0 = 61.5\)。讀者可以自行檢視有閱讀指定教材的學生成績，驗證會不會得到相同的結論。

其實還有更直觀的方法，可以更進一步地確立變異數分析等同於迴歸。仔細閱讀迴歸分析的輸出報表，會發現 attend 與 reading 這兩個變項的 p 值，與先前變異數分析所輸出的數值完全相同。這或許有些令人意外，因為迴歸模型計算的是 t 統計值，而 ANOVA 計算的卻是 F 統計值。不過，如果讀者們還記得 單元 7 的說明，應該會知道 t 分配與 F 分配之間其實有密切關係。若有一個數值服從自由度為 k 的 t 分配，將之平方後，這個新的數值會服從自由度為 1 與 k 的 F 分配。透過迴歸模型報表的t統計值，我們可以來驗證這一點。以 attend 變項為例，t值為4.65。將此數值平方後，便會得到 21.6，這個數值正好與 ANOVA 報表對應的 F 統計值相符。

最後還有一件事值得一提。因為 jamovi 開發團隊了解 ANOVA 與迴歸分析都是線性模型，所以使用者可以從迴歸模型中，輸出傳統的 ANOVA 表格。操作步驟：「線性迴歸 (Linear Regression)」–「模型係數 (Model Coefficients)」–「整體檢定 (Omnibus Test)」–「ANOVA 檢定 (ANOVA Test)」。執行後便會得到如 圖 14.19 展示的表格。

圖 14.19: 使用 jamovi 迴歸分析輸出整體 ANOVA 檢定結果 (Omnibus ANOVA Test)

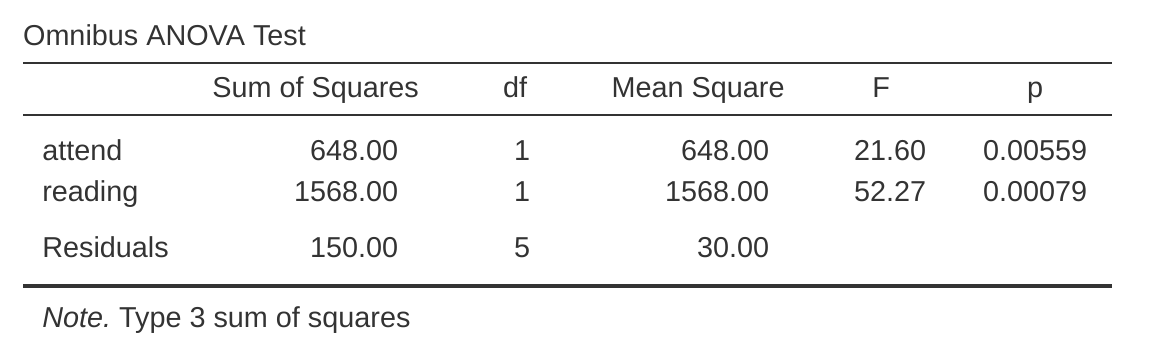
14.6.3 如何編碼因子設計的多重比較

至此，本書已經展示如何將 \(2 \times 2\) 的變異數分析 視做線性模型處理，這個概念也很容易延伸至 \(2 \times 2 \times 2\) 或 \(2 \times 2 \times 2 \times 2\) 的變異數分析，原理是相同的：只要當每一個因子都是一個二元變項即可。然而，當我們要處理有兩個以上水準的因子，情況就變得棘手一些。舉例來說，本單元稍早使用的示範資料 clinicaltrial.csv ，需要處理 \(3 \times 2\) 變異數分析，我們要如何將具有三個水準的「藥物」因子，轉換為迴歸模型的形式呢？

其實解決方法相當簡單：我們只要先了解一個概念，即一項有三個水準的因子，可以用兩個二元變項重新定義。 舉例來說，假設我們要建立一個新的二元變項名為 druganxifree 。當 drug 變項的值為 “anxifree” 時，我們便將 druganxifree 設為 1，否則設為 0。如此一來，這個變項便建立了一項對比 (contrast)，以此例來說，代表藥物”anxifree” 與另外兩種藥物之間的對比。 當然，單靠 druganxifree 一項對比，並不足以完全捕捉 drug 變項的所有資訊。我們還需要第二項對比，來區分 “joyzepam” 與安慰劑。為此，我們可以建立名為 drugjoyzepam 的第二項二元對比，當藥物是 “joyzepam”，其值就是1，否則為 0。結合這兩個對比，便能完美地區分所有三種可能的藥物。 表 14.10 展示如何用兩項對比的編碼代表三種藥物。

表 14.10:

用以區分三種藥物的二元對比編碼

drug	druganxifree	drugjoyzepam
"placebo"	0	0
"anxifree"	1	0
"joyzepam"	0	1

若病患服用的藥物是安慰劑，那麼這兩項對比的編碼都會是 0。若服用的是 Anxifree，則 druganxifree 變項為 1，drugjoyzepam 為 0。Joyzepam 的情況則正好相反：drugjoyzepam 為 1，而 druganxifree 為 0。

使用 jamovi 建立對比變項並不困難，只要使用「新增計算變項 (Compute New Variable)」功能就能完成。舉例來說，若要建立 druganxifree 這個變項，只要在公式欄位中輸入邏輯條件式：IF(drug == 'anxifree', 1, 0)

同樣地，建立 drugjoyzepam的邏輯條件式就是：IF(drug == 'joyzepam', 1, 0) 設定CBTtherapy 的對比變項也是一樣的方式：IF(therapy == 'CBT', 1, 0) 讀者可以在 jamovi 資料檔 clinicaltrial2.omv中，看到這些新增的變項以及其對應的邏輯條件式。

至此，我們已示範如何將一個有三個水準的因子，重新編碼為兩個二元變項。如同前一小節的介紹，變異數分析與迴歸處理二元變項的運算邏輯是相同的。然而，這種做法也會增加一些運算複雜度，這是下一節要討論的內容。

14.6.4 為什麼變異數分析等同於非二元因子迴歸分析

至此，clinicaltrial這筆資料有兩種版本：一個是原始資料 (clinicaltrial.csv)，其中的 drug 變項是一個三水準的因子；其二是擴充後的資料 (clinicaltrial2.omv)，其中的 drug 變項重新定義為兩個二元對比變項。接下來，我們想證明的是原先處理 \(3 \times 2\) 因子設計的變異數分析模型，等同以二元對比變項取代原始變項的迴歸模型。讓我們先重新執行變異數分析，結果列在 圖 14.20 。

圖 14.20: clinicaltrial資料的ANOVA 結果表(無交互作用項)

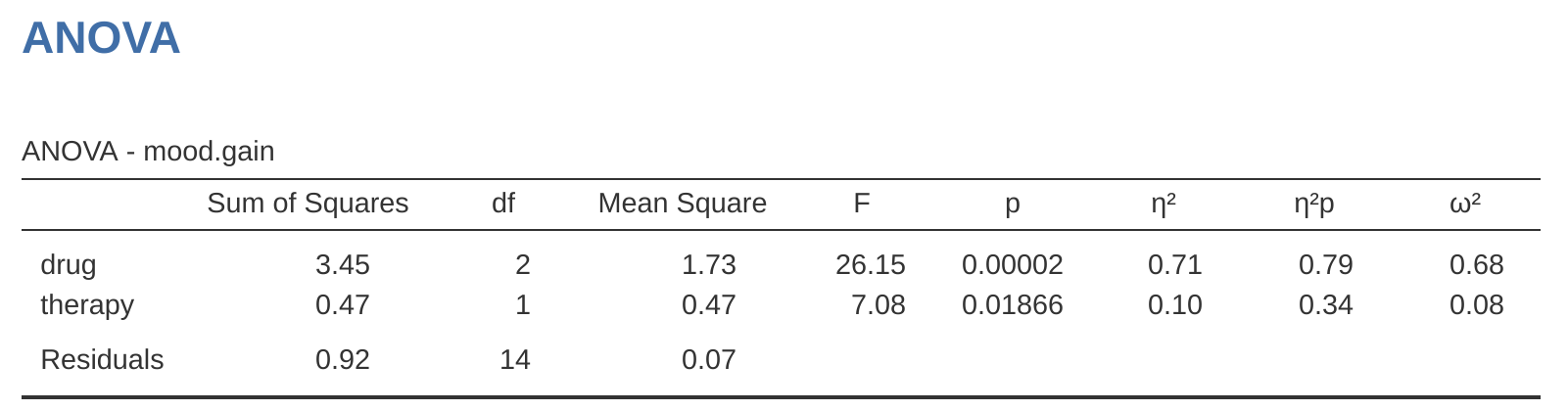
因為這個結果與前面執行過的變異數分析完全相同，很顯然沒有什麼要再補充說明的。接著改用druganxifree、drugjoyzepam與 CBTtherapy作為預測變項執行迴歸分析。結果展示在 圖 14.21 。

圖 14.21: clinicaltrial資料的迴歸分析結果表，包含對比變項 druganxifree 和 drugjoyzepam

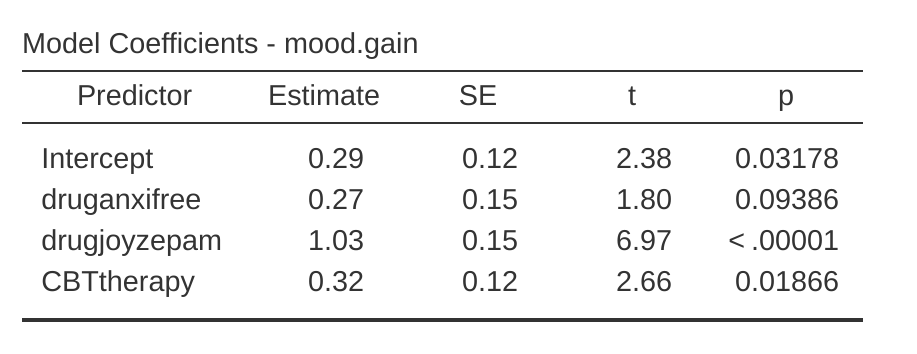
嗯，這個新輸出的表格與前一個完全不同。不出我們的預期，迴歸分析的報表會分開呈現三個預測變項的結果，如同之前曾做過的迴歸分析。一方面，我們可以看到 CBTtherapy 變項的 p 值，與變異數分析報表裡的 therapy p 值完全相同，這讓我們能確認迴歸模型處理這個變項的方式，與變異數分析是一樣的。另一方面，迴歸模型將 druganxifree 與 drugjoyzepam 這兩個對比變項分別進行檢定，彷彿兩者是完全無關的變項。

這種處理方式並不令人意外，因為迴歸模型不可能意識 drugjoyzepam 與 druganxifree 是來自重新編碼 drug的三個水準，所構成的兩個對比。對迴歸模型來說，這兩個變項之間的關聯性，跟 drugjoyzepam 與 CBTtherapy 之間沒什麼兩樣。然而，我們心知肚明，我們真正關心的並非這兩個對比是否各自顯著，而是想知道 drug 這個因子有沒有顯現整體效果。

也就是說，我們要用 jamovi 執行某種模型比較檢定 (model comparison test)，這個檢定能將兩個與「藥物」相關的對比項綁在一起進行評估。聽起來很熟悉吧？只要指定一個只包含 CBTtherapy 這個預測變項的虛無模型 (null model)，而且這個虛無模型不要納入兩個與代表藥物的二元對比變項即可，參考 圖 14.22 的示範。

圖 14.22: 迴歸分析的模型比較，模型 1(虛無)對比模型 2(含藥物變項)

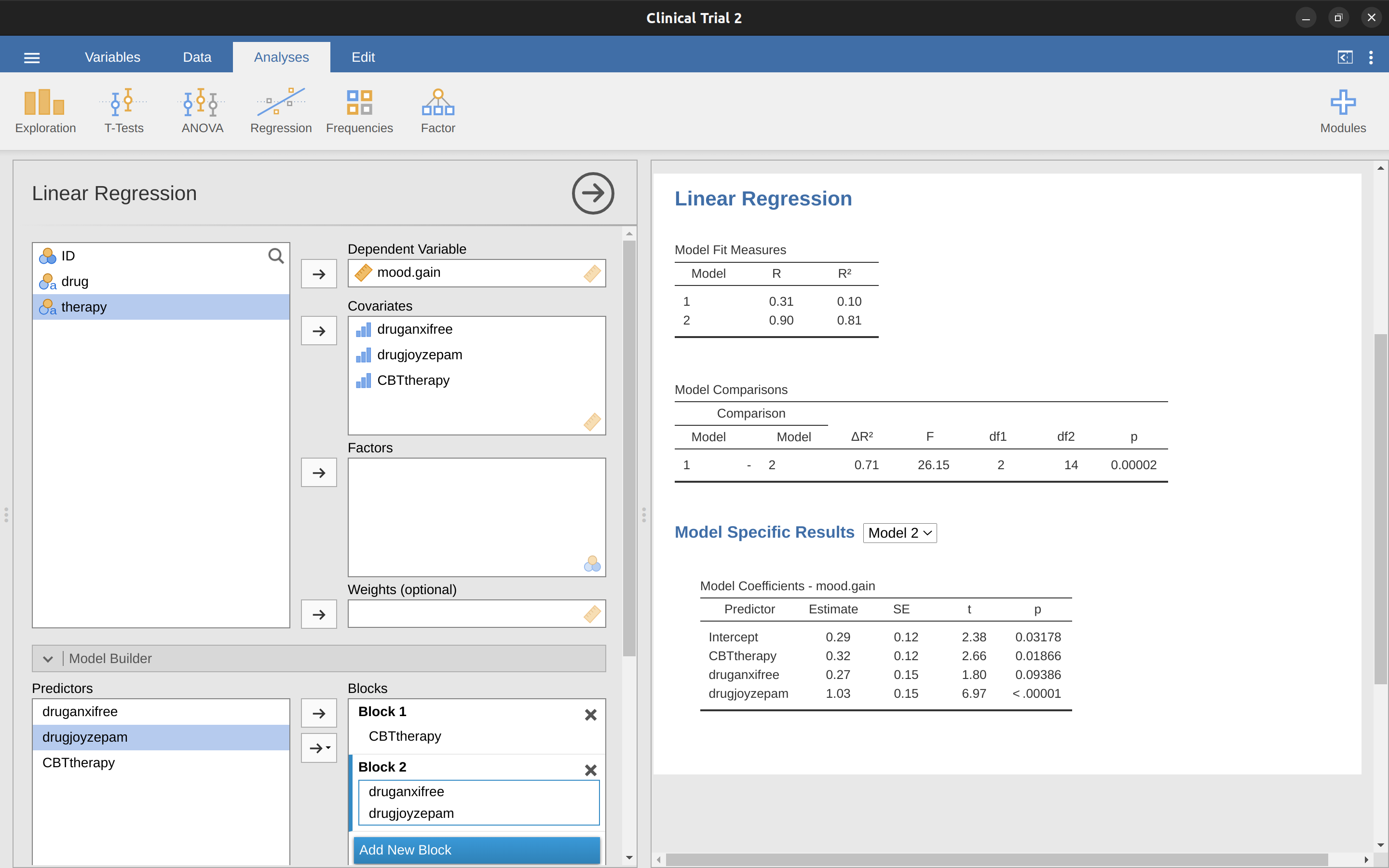
啊，這樣看起來好多了。報表的 F 統計值為 26.15，自由度為 2 與 14，p 值為 0.00002。這些數值與原先ANOVA報表的drug 主要效果所得到的數值完全相同。因此再一次證實，變異數分析與迴歸分析本質上是同一回事。它們都是一種線性模型，而且變異數分析的底層統計機制與迴歸模型分析的機制完全相同。理解這個事實是非常重要的，因為本章的剩餘部分的學習，將會相當依賴這個概念。

雖然為了證明變異數分析與迴歸模型的底層機制相同，我們大費周章地在 jamovi 建立兩個新的對比變項 druganxifree 與 drugjoyzepam，其實 jamovi 的線性迴歸分析模組，有一個更便捷的做法，參考 圖 14.23 的示範。

jamovi 模組設計的巧妙之處，在於它允許使用者直接將要設定為因子的預測變項，直接當作因子(factor)加入模型！很聰明吧！使用者還可以設定參考水準 (Reference Levels)，指定要以哪一組作為比較的基準。這裡我們分別設定為 placebo 與 no.therapy，因為這樣最能詮釋結果的意義。

圖 14.23: 包含所有因子和對比的迴歸分析，包括整體變異數分析檢定結果

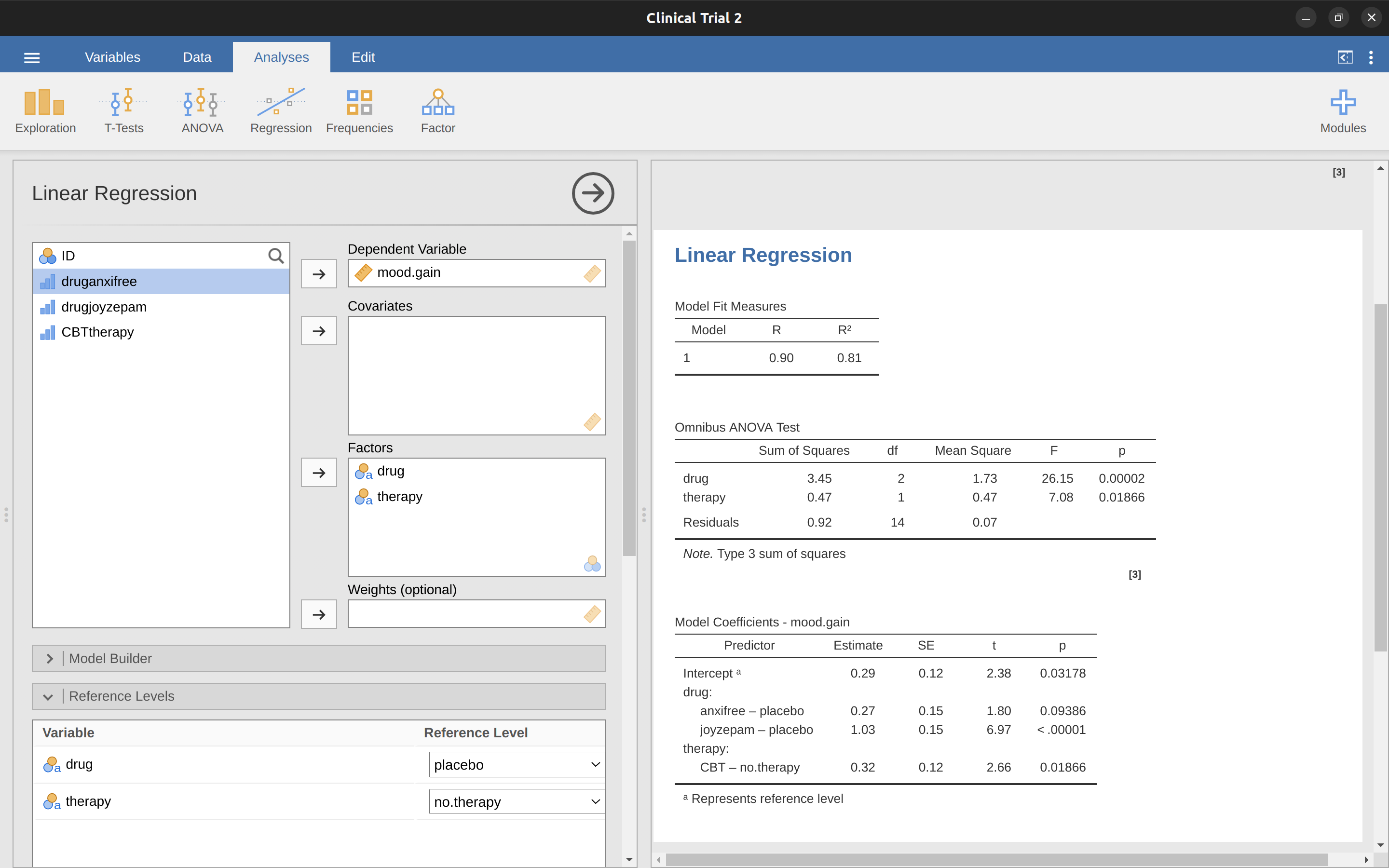
若是再開啟選單「模型係數 (Model Coefficients)」，點選「整體檢定 (Omnibus Test)」下方的「ANOVA 檢定 (ANOVA Test)」，便會看到 圖 14.23 所展示的報表：F 統計值為 26.15，自由度為 2 與 14，p 值為 0.00002。這些數字與我們原始 ANOVA 表格的drug 主要效果所得到的數值完全相同。這裡再次驗證ANOVA 與迴歸本質上是同一回事。

14.6.5 自由度就是計算有多少參數

終於，到了這裡可以給出一個令人滿意的自由度定義了：自由度就是模型中需要被估計的參數 (parameters) 個數。就迴歸模型或 ANOVA 而言，參數的個數即對應的迴歸係數 (即 b 值) 數量，其中也包含截距項。請讀者記住，任何 F 檢定，都必然是兩個模型之間的比較，第一個自由度 (\(df_1\))的意義就是兩個模型參數個數之間的差異值。舉例來說，前一小節示範的比較模型步驟裡，虛無模型 (mood.gain ~ therapyCBT) 有兩個參數：一個是 therapyCBT 變項的迴歸係數，另一個是截距項。而對立模型 (mood.gain ~ druganxifree + drugjoyzepam + therapyCBT) 則有四個參數：三個對比變項各有一個迴歸係數，再加上一個截距項。因此，這兩個模型之間參數數量差異便是自由度 \(df_1 = 4 - 2 = 2\)。

那麼，在某些看似沒有虛無模型的案例，該如何理解自由度的意義呢？例如，jamovi 線性迴歸分析的「模型配適度 (Model Fit)」功能，也有做 F 檢定。之前我們說過這對「整個迴歸模型」的檢定。然而，實際上這依然是兩個模型之間的比較。這種狀況的虛無模型是一個只包含 1 個迴歸係數 (即截距項) 的最簡模型。對立模型則包含 \(K + 1\) 個迴歸係數 (K 個預測變項加上截距項)。因此，這個 F 檢定的自由度，就是 \(df_1 = (K + 1) - 1 = K\)。

那麼 F 檢定的第二個自由度 (\(df_2\)) 又代表什麼呢？這個自由度永遠都與殘差有關。我們同樣也可以從參數的角度來思考如何解釋，不過可能有點違反一般人的直覺。

各位可以這麼想：假設整個研究的觀測值總數為 N。想要模型「完美地」描述這 N 個數值，我們就需要…不用懷疑，N 個參數。當我們建立一個迴歸模型時，其實就是嘗試用其中一部分參數，能夠完美地描述整體資料。若模型有 K 個預測變項與一個截距項，就是代表我們已經用掉了 \(K+1\) 個參數。如果不繼續深究具體細節，我們還需要多少個參數，才能將這個含有 \(K+1\) 個參數的迴歸模型，轉變為一個能完美重現原始資料的模型呢？若是讀者心中想的是 \((K + 1) + (N - K - 1) = N\)，所以答案必然是 \(N - K - 1\)——恭喜你，你答對了！

原則上，我們可以想像一個最複雜的迴歸模型，每一個資料點都是模型的一個參數，如此能完美地描述資料。這個「完整模型」會包含 N 個參數。而這裡所關心的殘差自由度，便是這個完整模型所需的參數個數 (N)，與我們實際接受的較簡潔模型所使用的參數個數 (\(K+1\)) 之間的差異值。因此，F 檢定中的第二個自由度便是 \(df_2 = N - (K + 1)\)，也就是 \(N - K - 1\)。這裡的 K，是指迴歸模型包含的預測變項個數，在 ANOVA 則是指二元對比變項的個數。以前一小節討論的範例來說，資料集有 \(N=18\) 個觀測值，而 ANOVA 模型有 \(K+1=4\) 個迴歸係數 (3 個對比變項 + 1 個截距)，因此殘差自由度為 \(df_2 = 18 - 4 = 14\)。

14.7 各種多重比較方案

前一節已經展示一種將因子轉換為數個對比組合的方法。我們用這個方法指定一組二元變項，並定義如同 表 14.11 展示的變項編碼。

表 14.11:

用以區分三種藥物的二元對比編碼

drug	druganxifree	drugjoyzepam
"placebo"	0	0
"anxifree"	1	0
"joyzepam"	0	1

表格中的每一行，對應因子的其中一個水準；每一列，則對應一個對比。這個表格的行數永遠比列數多一，這樣的表格有一個特殊的專有名詞：對比矩陣 (contrast matrix)。

設定對比矩陣的方式其實有很多種。這一節將討論幾種統計學家常用的標準對比矩陣，以及如何在 jamovi 設定對比矩陣。若讀者打算接著學習 小單元 14.10 ，仔細閱讀這一節會很有幫助。反之，若無此打算，大致看過即可，因為就平衡設計而言，對比方式怎麼設定並不太重要。

14.7.1 比較操作效果

先前所描述的對比編碼，我們設想某一個水準是特殊的，被當作是因子水準之間的基準線 (baseline)，例如前述範例的「安慰劑」。至於其他水準的編碼，都是根據這個基準線。這種對比編碼有個專有名稱，稱為處理對比 (treatment contrasts)，有時也被稱做虛擬編碼 (dummy coding)。這種對比編碼的每一個因子水準，都會與一個參考基準線相互比較，而這條基準線，就是截距項的數值。

之所以會這樣稱呼，是因為當因子中的某一水準確實是代表基準數值，採用這種對比編碼便會相當自然合理。這在臨床試驗範例資料是說得通的：「安慰劑」這個條件對應的是不給予受試者任何真正藥物的情境，因此可以做為基準線。另外兩個藥物條件，都是相對於安慰劑來做編碼：一個是用 Anxifree 取代安慰劑，另一個是用 Joyzepam 取代安慰劑。

這一節開頭展示的表格，是一個因子有三個水準的處理對比矩陣。但要怎麼設定有五個水準的因子處理對比矩陣呢？建議設定可參考 表 14.12 。

表 14.12:

因子有五個水準的處理對比矩陣

Level	2	3	4	5
1	0	0	0	0
2	1	0	0	0
3	0	1	0	0
4	0	0	1	0
5	0	0	0	1

在這個範例裡，第一個對比是水準 2 與水準 1 的比較，第二個對比是水準 3 與水準 1 的比較，依此類推。請注意，在預設情況下，因子的第一個水準，永遠會被視為基準線，也就是整列是 0、沒有自身對比項的那一組。jamovi 的使用者可以透過調整「資料變項 (Data Variable)」選單的變項水準順序，來指定要將哪一個水準設為因子的基準線。請在試算表欄位中，對變項名稱雙擊滑鼠左鍵，即可開啟「資料變項」視窗。

14.7.2 Helmert 比較法

處置對比在許多研究案例中都很有用，但它最適用的狀況，是當因子中確實存在一個基準組別，且研究者的目的，是想將所有其他組別都與該基準組別進行比較時。然而，在某些情況裡，並不會存在一個能做比較的基準類別，這時比較每組與先前的所有組別平均數，可能更有意義。

這便是可發揮 Helmert 對比 (Helmert contrasts) 的狀況。 jamovi 使用者可透過「變異數分析 (ANOVA)」–「對比 (Contrasts)」選單裡的 helmert 選項來設定。Helmert 對比的概念，是比較每一組與「先前」的所有組平均數。也就是說，第一個對比是比較第 2 組與第 1 組；第二個對比是比較第 3 組與第 1、2 兩組的平均數，依此類推。對於因子有五個水準的狀況，Helmert 對比矩陣的設定如同 表 14.13 示範。

表 14.13:

因子有五個水準的 Helmert 對比矩陣

1	-1	-1	-1	-1
2	1	-1	-1	-1
3	0	2	-1	-1
4	0	0	3	-1
5	0	0	0	4

Helmert 對比的一種實用特性，是每一個對比項的總和皆為零，也就是矩陣中各列的總和均為零。這種特性帶來的好處是：當我們將 ANOVA 當成迴歸模型時，採用 Helmert 對比，截距項所對應的數值就是全部資料的總平均數 (\(\mu_{..}\))。與處置對比的不同處是，後者的截距項對應的是基準類別的組別平均數。

這種特性在某些情況下非常有用。雖然本書至今示範的平衡設計資料裡，這個特性不是那麼重要，但後續如果要學習 小單元 14.10 ，將變得至關重要。其實，我們之所以不厭其煩地介紹這套編碼，主要原因便是：若讀者想透徹理解不平衡設計的 ANOVA，對比編碼的概念將是關鍵。

14.7.3 簡單比較

第三種要稍做介紹的對比編碼，稱為「和為零對比 (sum to zero contrasts)」，jamovi 功能選單的選項是「簡易對比 (Simple)」。這種功能被用來建構組別之間的成對比較 (pairwise comparisons)。具體來說，每一個對比的編碼，都是某個組別與基準類別之間的差異；這種對比編碼的基準類別，對應的是第一個組別 (表 14.14)。

表 14.14:

因子有五個水準的和為零對比矩陣

1	-1	-1	-1	-1
2	1	0	0	0
3	0	1	0	0
4	0	0	1	0
5	0	0	0	1

編碼方式與 Helmert 對比非常相似，對比矩陣的每一列總和也是零，這代表當 ANOVA 被視為迴歸模型時，截距項所對應的也是總平均數。在詮釋對比結果時，使用者要認知到，每一個對比都是第一組與其他其中一組之間的成對比較。具體而言，對比 1 代表的是「第 2 組減去第 1 組」的比較；對比 2 代表「第 3 組減去第 1 組」的比較，依此類推。⁷

14.7.4 jamovi的對比選項

jamovi 的 ANOVA 分析模組內建多種可產生各種對比編碼的選項。使用者可以在各種ANOVA主選單裡，從「對比 (Contrasts)」次選單中找到這些選項，如 表 14.15 列出的說明：

表 14.15:

jamovi ANOVA 分析模組可用的對比類型

Contrast type
Deviation	Compares the mean of each level (except a reference category) to the mean of all of the levels (grand mean)
Simple	Like the treatment contrasts, the simple contrast compares the mean of each level to the mean of a specified level. This type of contrast is useful when there is a control group. By default the first category is the reference. However, with a simple contrast the intercept is the grand mean of all the levels of the factors.
Difference	Compares the mean of each level (except the first) to the mean of previous levels. (Sometimes called reverse Helmert contrasts)
Helmert	Compares the mean of each level of the factor (except the last) to the mean of subsequent levels
Repeated	Compares the mean of each level (except the last) to the mean of the subsequent level
Polynomial	Compares the linear effect and quadratic effect. The first degree of freedom contains the linear effect across all categories; the second degree of freedom, the quadratic effect. These contrasts are often used to estimate polynomial trends

14.8 事後檢定

現在轉換一下主題。有別於使用「對比」來檢定事前計畫的比較，假如我們執行了 ANOVA ，而且發現結果具有顯著效果。由於 F 檢定是一種「總括檢定 (omnibus test)」，它只告訴我們「所有組別平均數皆相等」這個虛無假說不成立，但是無法得知是哪幾組之間彼此不同。單元 13 曾經討論過這個課題，那裡介紹的解決方案，是為所有可能的組別配對都執行一次 t 檢定，並透過多重比較校正 (例如 Bonferroni 或 Holm 法) 來控制整體的型一錯誤率 (Type I error rate)。這個方法的優點是相對單純，而且適用多種需要檢定複數假設的情境；但是若要在多因子研究的狀況進行有效率的事後比較 (post hoc testing)，這種方法未必是最佳選擇。統計文獻中存在著非常多種執行多重比較的方法 (Hsu, 1996)，逐一詳細介紹會超出這本入門教科書的範圍。

話雖如此，本書仍想特別介紹一套事後檢定方法，就是 Tukey 的「誠實顯著差異法」，簡稱 Tukey’s HSD。在這裡，我們將省略介紹公式，專注在理解背後的概念。Tukey’s HSD 的基本概念，是檢視所有相關組別之間的成對比較；也因此，只有在研究者所關心的確實是成對差異時，才合適使用 Tukey’s HSD 。⁸舉例來說，分析clinicaltrial.csv 資料集的因子設計ANOVA，在指定了「藥物」與「治療」兩個主要效果後，我們所關心的，便是以下四組的成對比較：

• Anxifree vs. 安慰劑，兩組在情緒改善程度上的差異。
• Joyzepam vs. 安慰劑，兩組在情緒改善程度上的差異。
• Anxifree vs. Joyzepam，兩組在情緒改善程度上的差異。
• CBT 治療 vs. 無治療，兩組在情緒改善程度上的差異。

對於任何一組的比較，我們感興趣的都是各組別所代表的母群，所估計的平均數之間真實差異。Tukey’s HSD 會運算全部四組比較，建構同步信賴區間 (simultaneous confidence intervals)。所謂 95%「同步」信賴區間的意思是：若我們重複這項研究非常多次，在 95% 的研究結果中，所有資料建構的信賴區間，都會同時包含所對應的真實參數值。此外，我們也可以利用這些信賴區間，來計算任何一種特定比較的校正後 p 值。

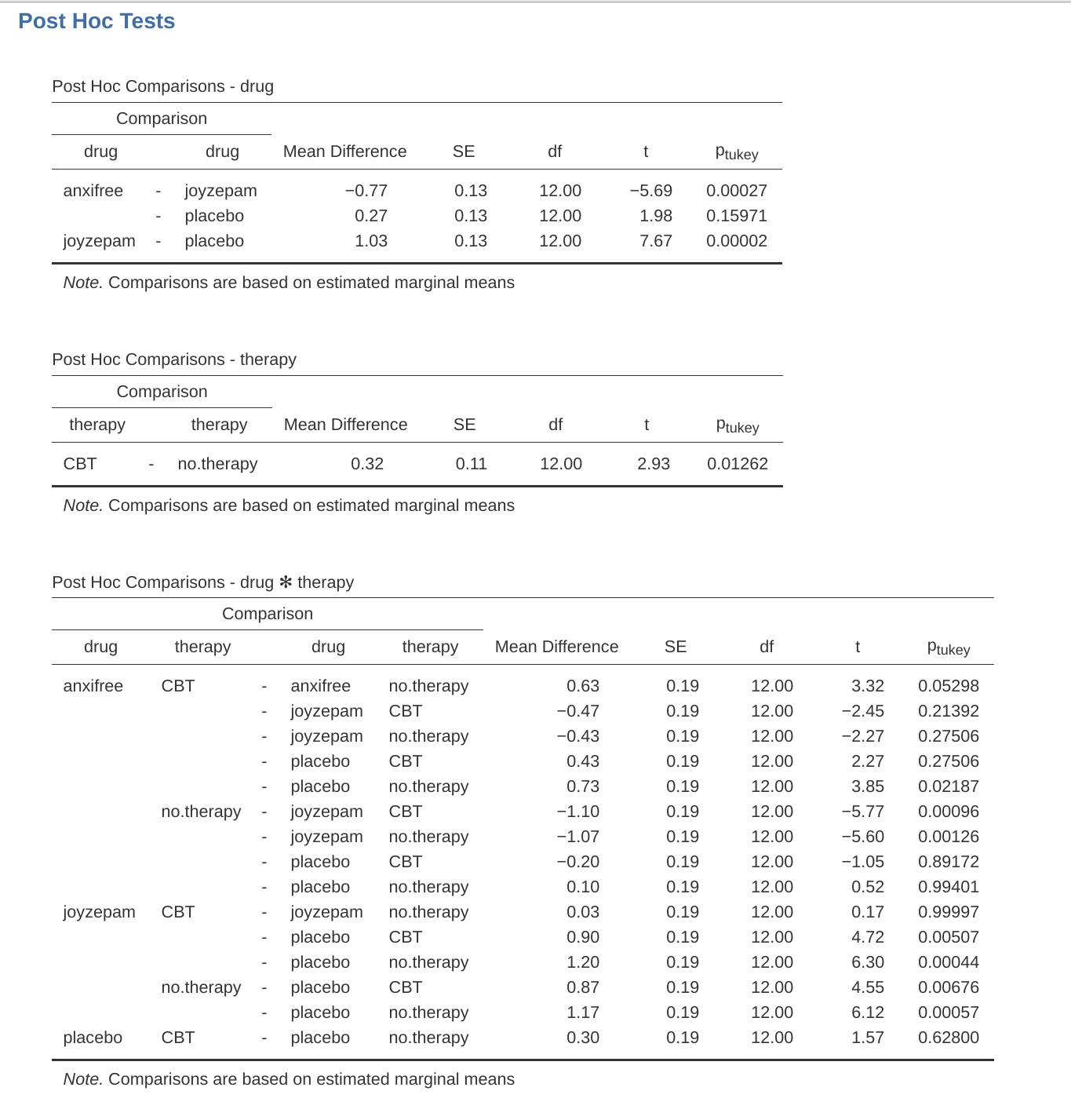
用 jamovi 執行 Tukey HSD 相當容易。使用者只需指定針對哪一個 ANOVA 模型的特定項，要進行事後比較。舉例來說，若我們想針對主要效果進行事後比較，並且不考慮 交互作用 ，操作步驟是：在 ANOVA 的分析視窗，點開「事後比較 (Post Hoc Tests)」次選單，將 drug 與 therapy 這兩個變項移至右方的對話框，然後從可用的校正方法選項，勾選「Tukey」。執行完成的結果報表，如同 圖 14.24 展示。

圖 14.24: jamovi 因子設計ANOVA 的 Tukey HSD 事後比較 (模型不含交互作用項)

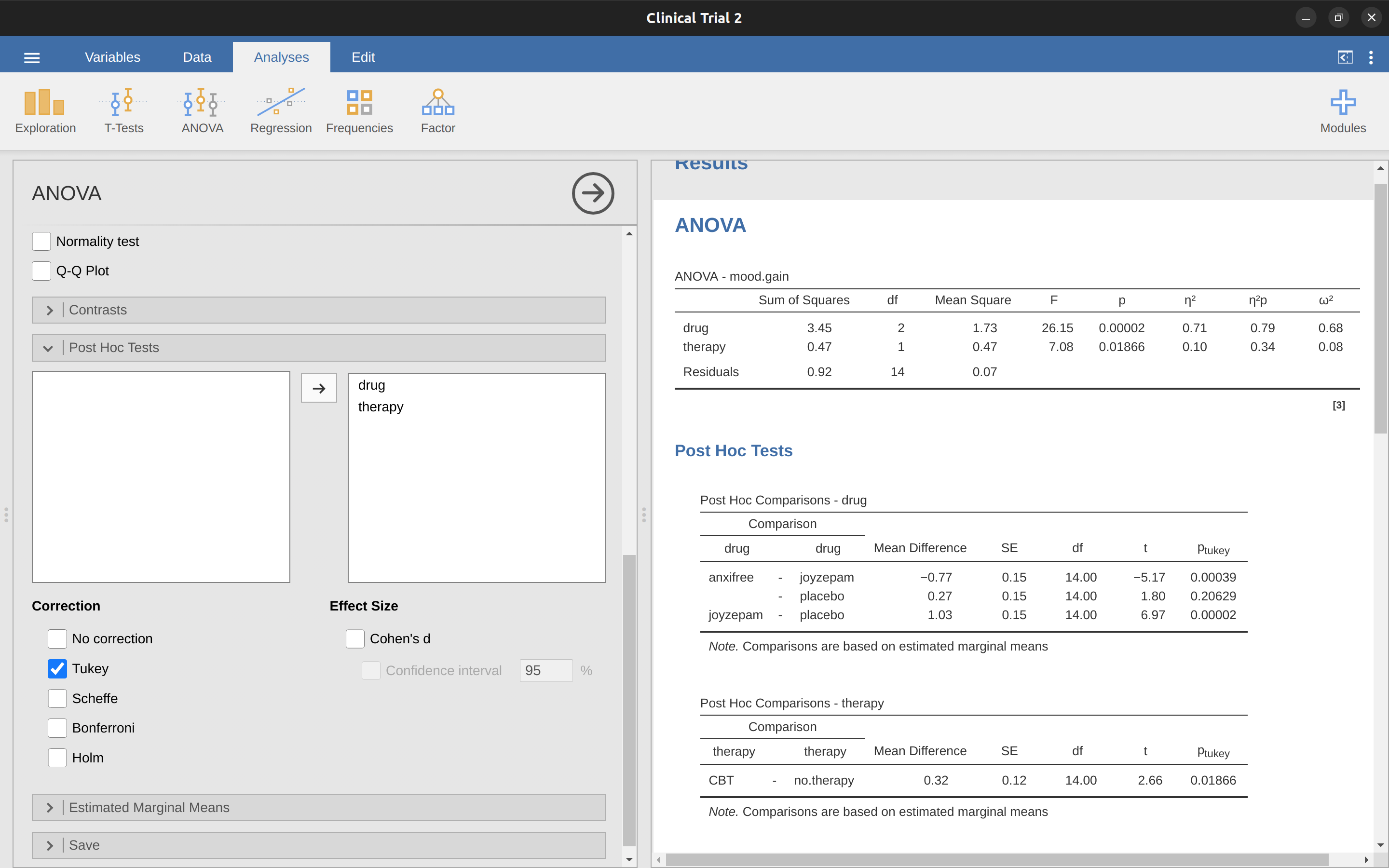
「事後比較」結果報表的內容相當簡單明瞭。舉例來說，第一組比較的是 Anxifree 與安慰劑的差異，報表的第一部分顯示，兩組平均數的觀測差異值為 .27。下一個數值是差異的標準誤，雖然目前版本的 jamovi 尚未直接提供，但是讀者若有需要，可以據此計算出 95% 信賴區間。接著依序是自由度、t 統計值，以及 p 值。從表格內容可以知道，第一組比較的校正後 p 值為 .21。相對地，下一行顯示 Joyzepam 與安慰劑的觀測差異值為 1.03，且此結果達到顯著水準 (\(p < .001\))。

目前為止，一切順利。那麼，如果分析模型有交互作用項時，要如何處理呢？舉例來說，jamovi 的預設選項，便是設定「藥物」與「治療」之間存在交互作用。在這種情況，我們需要考慮的成對比較數量便會開始增加。

如前所述，我們還是要考慮與「藥物」主要效果相關的三組比較，以及與「治療」主要效果相關的唯一一組比較。但是要探討交互作用顯著的原因時，就要找出是哪些組別的差異，造成了交互作用顯著，便需考慮以下的比較組合：

• 使用 Anxifree 且接受 CBT 治療者 vs. 使用安慰劑且接受 CBT 治療者，兩者在情緒改善程度上的差異。
• 使用 Anxifree 且未接受治療者 vs. 使用安慰劑且未接受治療者，兩者在情緒改善程度上的差異。
• …以此類推。

我們會發現需要考慮的比較組合數量相當多。因此，對這個包含交互作用的 ANOVA 模型執行 Tukey 事後分析後，會發現它計算了大量的成對比較 (總計 19 組)，如同 圖 14.25 的展示。很明顯地，報表格式與前一個非常相似，只是比較的組數變得更多了。

圖 14.25: jamovi 因子設計ANOVA 的 Tukey HSD 事後比較 (模型包含交互作用項)

14.9 事前檢定方法

延續前面關於 ANOVA 中「對比」與「事後比較」的討論，本書認為計畫式比較 (planned comparisons) 也相當重要，值得在此簡單介紹。在關於多重比較方案的討論裡，包括這個單元，還有 單元 13 ，都是預設研究者所執行的是事後比較。舉例來說，在藥物改善情緒的示範案例裡，研究者可能預期不同藥物對情緒會有不同效果，也就是假設藥物的主要效果存在，但是對於「效果會如何不同」，以及「哪些成對比較值得探討」，並沒有任何具體的事前假設。在這種情況，確實就需要像 Tukey’s HSD 這類的事後比較方法。

然而，事前檢定的情況將會截然不同，如果研究者打從一開始要進行感興趣的特定比較，就會事先提出明確且具體的假說，並且絕對不打算探究任何事先指定範圍之外的比較。若是如此，且研究者能誠實、嚴格地堅守此「高尚的意圖」，不去執行任何額外的比較。就算是資料看起來，那些未曾預先設定假說的比較，呈現出誘人的顯著效果 (deliciously significant effects)，也不為所動。那麼採用像 Tukey’s HSD 這樣的方法便不太合理。因為 Tukey’s HSD 會對一整批研究者從未關心、也無意探究的比較，進行多餘的校正。在這種研究情境，研究者可以安心地執行有限數量的假說檢定，而無需進行多重比較校正。這種作法，便稱為「計畫式比較」，有時會應用於臨床試驗中。然而，更深入的探討已超出這本入門書的範圍，但至少，讀者現在知道有這類方法存在！

14.10 不平衡的因子設計分析

因子設計ANOVA 是一個相當實用的統計方法。數十年來，它一直是分析實驗資料的標準方法之一；讀者會發現，在心理學領域，閱讀大約兩三篇論文，就會看到 ANOVA 的統計資訊。然而，在實際的科學文獻中所見到的 ANOVA，與本書所描述的 ANOVA 有一個巨大的差別：在現實世界中，很少有研究案能執行完美的平衡設計 (balanced design)。出於種種原因，許多研究中，部分細格的觀測值數量，往往會比其他細格來得多。換言之，我們所身處的世界其實是充斥著不平衡設計 (unbalanced design)。

處理不平衡設計需要比處理平衡設計更加謹慎，要理解的統計理論也混亂許多。或許正是因為要了解的理論很雜亂，或者授課時間不夠，根據本書作者的經驗，大學部的心理學研究法課程，常有一種壞習慣，就是完全跳過這個課題。許多統計教科書對此課題通常是輕描淡寫。本書作者認為，這最終導致許多領域要處理統計實務的研究者，其實並不曉得不平衡設計的 ANOVA 存在數種相異的「類型」，各種類型其實會產出各自不同的結果。

最令人驚訝的是，多數心理學文獻報告的不平衡因子設計ANOVA 結果的論文，其實並未提供足以重現其分析的詳細資訊。作者私自懷疑，大多數研究者甚至沒有意識到，他們所用的統計軟體，後台預設值讓他們無意間避過許多重大的資料分析決策。細想起來，這其實有點恐怖。因此，若讀者想避免將資料分析的主控權，交給一套笨拙的軟體擺佈，就請繼續讀下去。

14.10.1 咖啡飲用資料

如同我們一路走來的風格，利用實際資料來學習會很有幫助。coffee.csv 這個資料檔是一筆\(3 \times 2\)的虛構資料集，可用不平衡設計 ANOVA 分析。假想我們要用這筆資料探討一個問題：人們喝了太多咖啡後變得很愛說話，究竟純粹是咖啡本身的效果，還是咖啡中所加的牛奶與糖也造成了影響？

假定我們找了 18 位受試者，請他們喝咖啡。咖啡因的含量是固定的，但我們操弄了兩個因子：第一個是「牛奶」，這是一個二元因子，有兩個水準：「加」與「不加」。第二個是「糖」，這是有三個水準的因子，分別是：「真糖」、「代糖 (人工甜味劑)」，以及「無糖」。結果變項babble是一個連續變項，用來衡量受試者「愛說話」的程度，其中具體的心理學意義是什麼，在此先不計較。這筆資料匯入 jamovi 試算表的內容，如同 圖 14.26 展示。

圖 14.26: jamovi 中的 coffee.csv 資料集，並依因子水準呈現描述統計

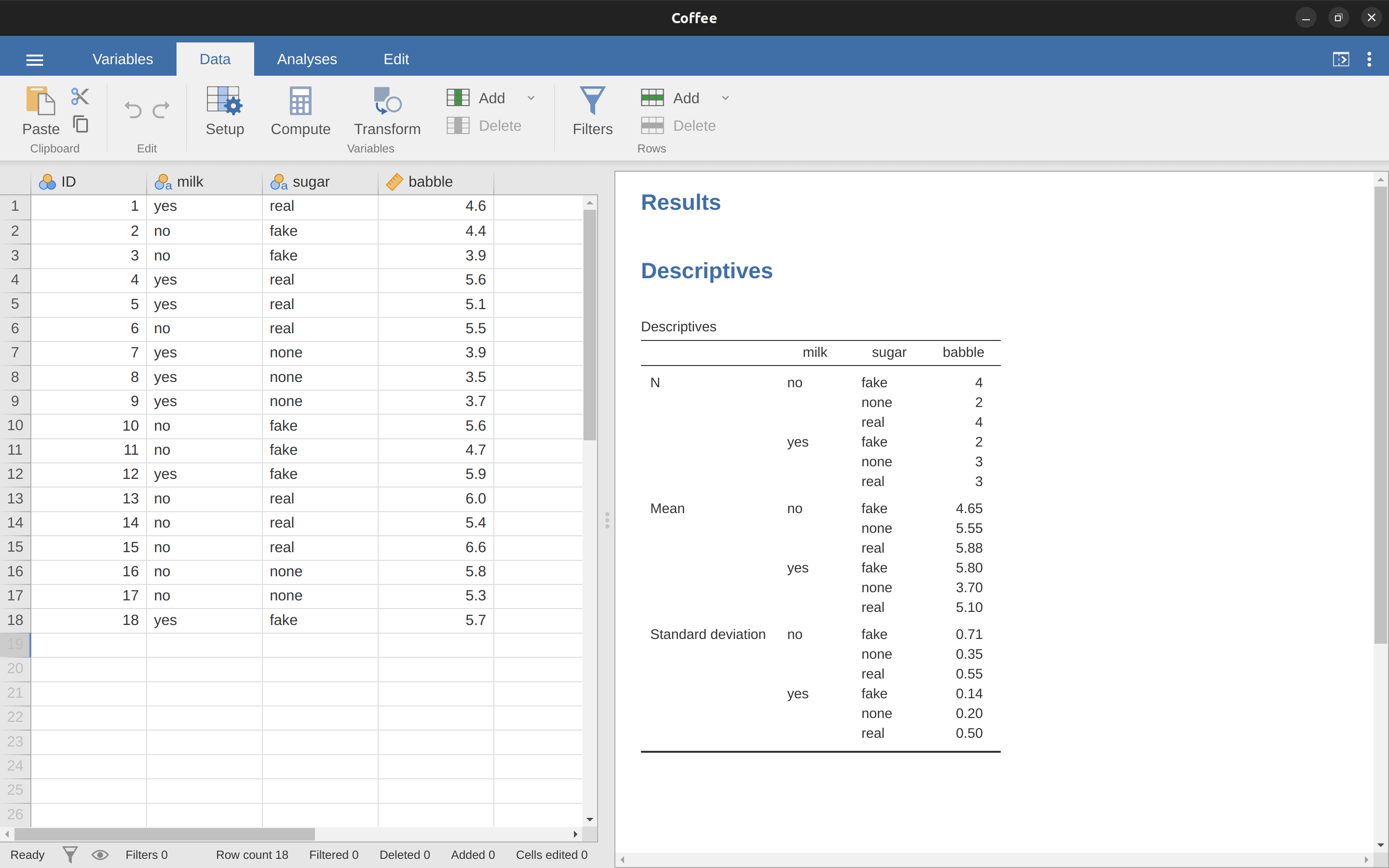
看過 圖 14.26 報表區的平均數表格，可以讓人強烈感覺到組別之間存在差異，特別是比較一下各組平均數與標準差，會發現標準差最小只有 .14，最大是 .71，相較於各組平均數之間的差異，這樣的數值差異是相當小的。⁹

乍看之下這筆資料使用因子設計ANOVA分析是理所當然，但是看過各組的觀測值個數之後，問題便浮現了。 圖 14.26 表格列出的各組 N 值可知，這筆資料違反最基本的適用條件：各組的受試者人數應相等。如何處理這種狀況，本書至今尚未真正討論。

14.10.2 不平衡設計不適用「標準變異數分析」

不平衡設計帶來一個有點令人不安的發現：其實世界上並沒有可以被稱為「標準 ANOVA」的存在。實際上，我們可以透過三種截然不同的方式¹⁰來處理不平衡設計ANOVA。如果是平衡設計，這三種方式會產生完全相同的結果，包括平方和 (SS)、F 值等，都會與本章一開始所討論的公式相同。然而用在不平衡設計，各種方法的計算結果便會不同。此外，並非所有方式都是適用於所有情境；某些方式會比其他方式更適合您的研究情境。有鑑於此，理解處理不平衡設計的各種 ANOVA 類型，以及它們彼此之間有何差異，是最重要的課題。

處理不平衡設計的第一種 ANOVA 類型，按照命名慣例，稱為第一型平方和 (Type I sum of squares)。讀者大概能猜到另外兩種類型的名稱。這個名稱中的「平方和」一詞，最初是出現在 SAS 統計軟體，後成為標準術語，但是這個名稱在某些地方會誤導使用者。

之所以會用不同類型的「平方和」來命名，背後邏輯或許是，使用者閱讀軟體產出的 ANOVA 表格時，最吸引注意力的數值就是SS。自由度並未改變，平方和平均 (MS) 依然是 SS 除以 df，以此類推。

然而，這個術語的不夠充分之處，在於它並未揭露各種 SS 內在各異的原因。有鑑於此，建議讀者將這三種類型的 ANOVA，理解為三種不同的假說檢定策略 (hypothesis testing strategies)。各種策略確實會導致不同的 SS 數值，但是我們要了解的重點是「策略」本身，而非 SS 的數值。

回顧 小單元 14.6 可以發現，任何一個 F 檢定，都是為了比較兩個線性模型的資料解釋能力是否不同。閱讀 ANOVA 表格的每一個 F 檢定值，務必記得都是對應一組要相互比較的模型。由此帶出一個問題：我們比較的究竟是「哪一組」模型呢？這便是第一類、第二類、與第三類 ANOVA 之間的根本差異：每一種類型各自對應一種為檢定選擇模型配對的方式。

14.10.3 第一型平方和

第一型平方和有時也會被稱為序列 (sequential)平方和，因為它來自將模型項逐一加入的過程。以 範例資料coffee.csv來說，假如要執行一個包含交互作用項的完整 \(3 \times 2\) 因子設計ANOVA，這個模型包含結果變項 babble、預測變項 sugar 與 milk，以及交互作用項 sugar × milk，模型公式可寫成 babble ~ sugar + milk + sugar × milk。第一型的策略就是循序漸進地建構這個模型，從最簡單的模型開始，逐步加入模型項。

這筆資料的最簡單模型，是假設 milk 與 sugar 對 babble 都不具任何效果，所以模型只有截距項，可寫成 babble ~ 1，也就是 小單元 14.6 提到的虛無假設模型。僅次於虛無假設的簡單模型，是只有兩個主要效果其中之一的線性模型。這裡有兩種選擇：可以先加入 milk，也可以先加入 sugar。稍後，我們會知道順序其實相當重要，不過目前我們先隨意選擇 sugar。因此，模型序列的第二個模型便是 babble ~ sugar，如此構成我們第一個檢定的對立假說。至此，我們便能進行第一個假說檢定 (表 14.16)。

表 14.16:

以 babble 為結果變項的虛無假說與對立假說

Null model:	\(babble \sim 1\)
Alternative model:	\(babble \sim sugar\)

這個比較代表針對 sugar 主要效果的假設檢定。模型建構的下一步，是加入另一個主要效果項，因此序列的下一個模型便是 babble ~ sugar + milk。這組模型形成第二個假設檢定 (表 14.17)。

表 14.17:

以 babble 為結果變項的第二組假說檢定

Null model:	\(babble \sim sugar\)
Alternative model:	\(babble \sim sugar + milk\)

這組模型比較構成對 milk 主要效果的假說檢定。從某個角度來看，這種方法非常「優雅」：第一個檢定的對立假說，直接成為了第二個檢定的虛無假說。正是如此的過程，第一型平方和的方法是如同字面意義的「序列性」，每一個檢定都是建立在前一個檢定的結果之上。然而，從另一個角度來看，這種方式非常「不優雅」，因為各組檢定之間存在著強烈的不對稱性：「sugar」主要效果的檢定 (第一個檢定) 完全忽略 milk，而「milk」主要效果的檢定 (第二個檢定) 卻將 sugar 納入比較。無論如何，模型序列的第四個模型，就是包含交互作用的完整模型 babble ~ sugar + milk + sugar × milk，對應的假說檢定如同 表 14.18 展示。

表 14.18:

以 babble 為結果變項的第三組假說檢定

Null model:	\(babble \sim sugar + milk\)
Alternative model:	\(babble \sim sugar + milk + sugar * milk \)

jamovi 的 ANOVA 模組預設值，是計算第三型平方和。因此，若要執行第一型平方和的分析，必須在「ANOVA」–「模型 (Model)」選項中，將「平方和 (Sum of squares)」次選單的預設值改為「第一型 (Type 1)」。這會產出如同 圖 14.27 展示的 ANOVA 表格。

圖 14.27: jamovi 採用第一型平方和生成的 ANOVA 結果表格

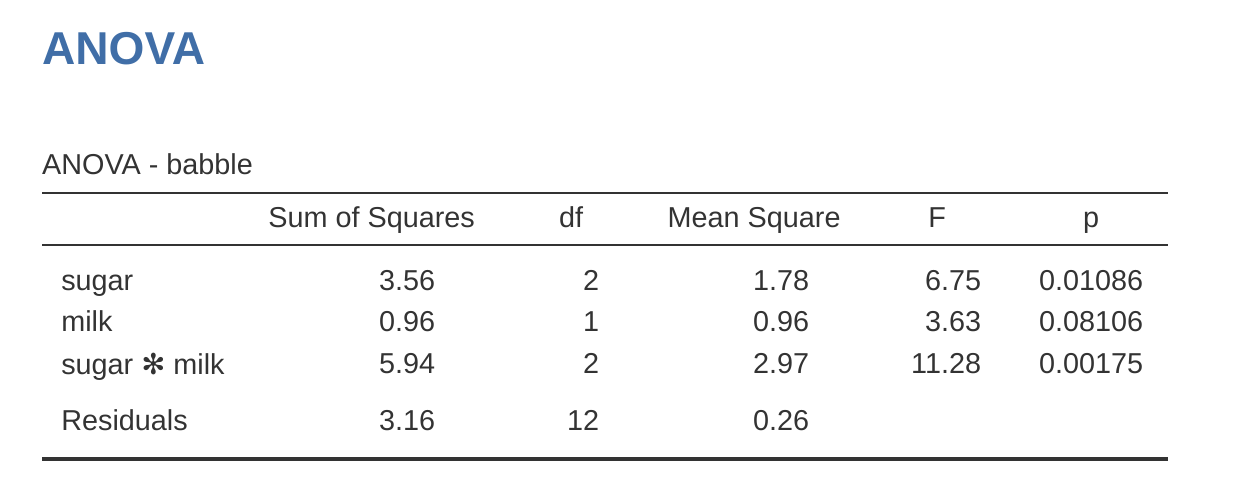
使用第一型平方和的最大問題，在於其結果會受到變項加入模型的順序所影響。然而，在許多實務狀況，研究者大多沒有任何理論依據，能說明為何某個排序是優先於另一個。這就是牛奶與糖問題反映的真實情況。我們應該先放牛奶，還是先放糖？這個數據分析問題，感覺就像點咖啡時一樣隨興。或許有些人對某種順序有堅定不移的看法，但很難想像這個問題存在著任何有可靠根據的答案。

然而，當我們改變加入變項的順序時 (參考 圖 14.28 )，看一看發生了什麼事：兩個主要效果的 p 值都改變了，而且改變幅度相當大。其中，milk 的效果甚至變得顯著。儘管我們已經知道，應避免對此結果變化下過強的結論。那麼，這兩份 ANOVA 報表(圖 14.27 或 圖 14.28 )，我們該呈現哪一份呢？答案並非顯而易見。

圖 14.28: jamovi 採用第一型平方和生成的 ANOVA 結果表格 (因子投入順序不同，milk 優先)

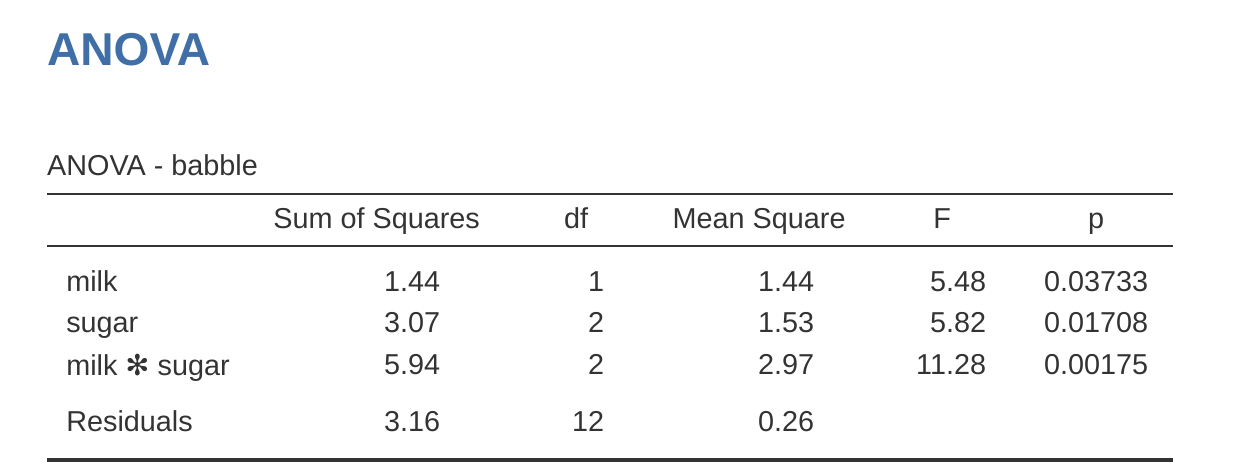
當我們檢視用來定義「第一個」與「第二個」主要效果的假說檢定時，會發現它們在本質上有所不同。在最初的範例中，sugar主要效果的檢定完全忽略了milk，而milk主要效果的檢定卻考量了sugar。因此，第一型的檢定策略，確實是將第一個加入的主要效果，賦予了某種凌駕於第二個主要效果之上的「理論優先性」。根據本書作者的經驗，現實中極少、甚至從未出現有任何理論優越性，能支持我們將兩個主要效果進行如此不對稱的處理。

這一切所導致的結論是：第一型檢定在多數情況下都不能回答我們真正感興趣的問題，因此，我們要來認識第二型與第三型。

14.10.4 第三型平方和

經過使用第一型平方和進行假設檢定的實例討論，讀者可能會認為接下來自然該談談第二型檢定。然而，在討論較為棘手的第二型之前，先來討論概念較簡單的第三型會更為自然，而且是 jamovi ANOVA 模組的預設選項。

第三型的基本概念相當單純：無論要評估模型的哪一個特定項，F 檢定的對立假設，永遠都是使用者所設定的完整 ANOVA 模型；而虛無假設，則是從完整模型移除被檢定的目標特定項之模型。以咖啡範例資料來說，完整模型是 babble ~ sugar + milk + sugar × milk。那麼，檢定「sugar」主要效果，便是比較 表 14.19 列出的兩個模型。

表 14.19:

以’babble’作為結果變量的零假設和替代假設，使用類型 III 平方和

Null model:	\(babble \sim milk + sugar * milk\)
Alternative model:	\(babble \sim sugar + milk +sugar * milk \)

同理，檢定「milk」的主要效果，就是比較「完整模型」與「移除 milk 的虛無模型」，如同 表 14.20 的展示。

表 14.20:

以’babble’作為結果變量的更多零假設和替代假設，使用類型 III 平方和

Null model:	\(babble \sim sugar + sugar * milk\)
Alternative model:	\(babble \sim sugar + milk +sugar * milk \)

最後要檢定「sugar × milk」的交互作用項，也是依循完全相同的方式：比較「完整模型」與「一個移除了 sugar × milk 交互作用項的虛無模型」，如同 表 14.21 展示。

表 14.21:

從以“babble”為結果變量的假設中刪除交互項，使用類型 III 平方和

Null model:	\(babble \sim sugar + milk\)
Alternative model:	\(babble \sim sugar + milk +sugar * milk \)

這些基本概念，可以延伸至處理設計更複雜的 ANOVA。舉例來說，如果我們的資料要處理包含 A、B、C 三個因子的 ANOVA，其中要檢定所有可能的主要效果與交互作用，包括三因子交互作用 A × B × C。 表 14.22 展示這種狀況的第三型檢定要比較的各組模型。雖然這張表格看起來有些嚇人，其實概念相當單純。在所有情況下，對立假說皆對應到包含三個主要效果項 (如 A)、三個雙因子交互作用 (如 A × B)，以及三因子交互作用 (A × B × C) 的完整模型。至於虛無假說，永遠都是從這 7 個項中移除目標效果項的那一個縮減模型。

表 14.22:

具有三個因素和所有主效應和交互項的類型 III 測試

Term being tested is	Null model is outcome ~ ...	Alternative model is outcome ~ ...
A	\(B + C + A*B + A*C + B*C + A*B*C \)	\(A + B + C + A*B + A*C + B*C + A*B*C \)
B	\(A + C + A*B + A*C + B*C + A*B*C \)	\(A + B + C + A*B + A*C + B*C + A*B*C\)
C	\(A + B + A*B + A*C + B*C + A*B*C \)	\(A + B + C + A*B + A*C + B*C + A*B*C \)
A*B	\(A + B + C + A*C + B*C + A*B*C \)	\(A + B + C + A*B + A*C + B*C + A*B*C \)
A*C	\(A + B + C + A*B + B*C + A*B*C \)	\(A + B + C + A*B + A*C + B*C + A*B*C \)
B*C	\(A + B + C + A*B + A*C + A*B*C \)	\(A + B + C + A*B + A*C + B*C + A*B*C \)
A*B*C	\(A + B + C + A*B + A*C + B*C \)	\(A + B + C + A*B + A*C + B*C + A*B*C \)

乍看之下，用第三型平方和做假設檢定似乎是個好方法。首先，它排除第一型檢定中所遇到的不對稱問題。而且，由於現在所有效果項都是用一樣的方式處理，假說檢定的結果，並不會受到效果項加入順序的影響，這無疑是一件好事。然而，在詮釋檢定結果時，特別是針對主要效果項，卻存在一個大問題。

我們再用 coffee 資料來說明。假設根據第三型的檢定結果，milk 的主要效果不顯著。這說明 babble ~ sugar + sugar*milk 這個模型，比完整模型更能配適資料。但這究竟代表什麼？如果 sugar*milk 這個交互作用項也不顯著，我們或許會傾向下結論說：資料顯示唯一重要的因子是 sugar。但假設我們得到的是一個顯著的交互作用，以及一個不顯著的 milk 主要效果。在這種情況下，我們應該認定真的存在「sugar 的效果」、也存在「milk 與 sugar 的交互作用」，卻不存在「milk 的效果」嗎？這聽起來太古怪了。

正確的答案必然是：當交互作用顯著時，去談論主要效果是沒有意義的。¹¹ 這似乎是多數統計學家的共識建議，本書作者也認為這是正確的建議。然而，若是交互作用顯著時，談論不顯著的主要效果是沒有意義的，那麼「為何第三型檢定要允許一個『包含交互作用項，卻移除了構成該交互作用之主要效果』的模型，來作為虛無假說」，這樣的前提就變得非常不合理了。當我們用這種方式來描述檢定結果時，第三型的虛無假設就真的沒什麼道理了。

稍後我們將會看到，第三型的檢定結果在某些實務情況，依然有其價值。但首先，讓我們先看一下採用第三型平方和的 ANOVA 結果表格，請見 圖 14.29 。

圖 14.29: 在 jamovi 中使用類型 III 和平方的 ANOVA 結果表

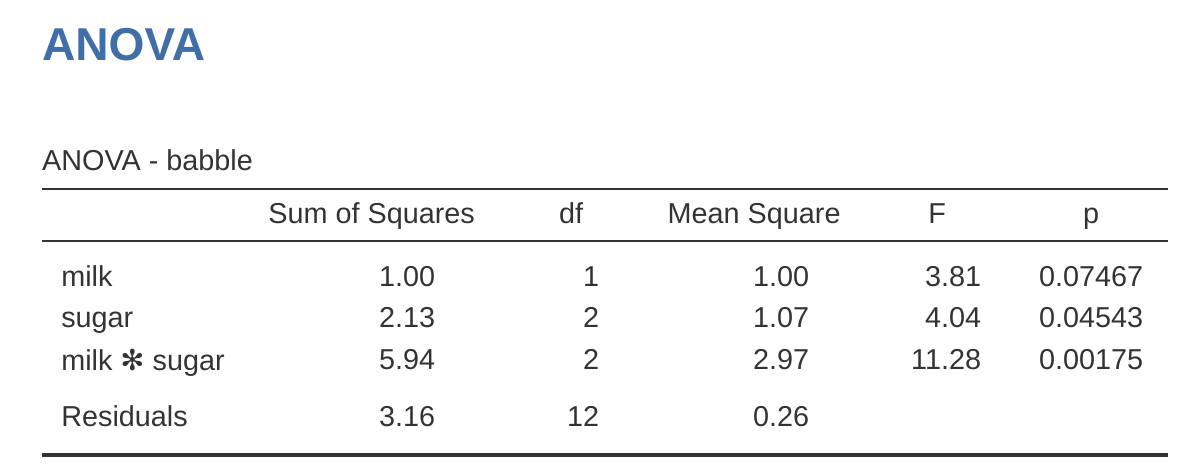
但請注意，第三型檢定策略有一個古怪的特性：一般來說，檢定結果會受到研究者用來編碼因子的「對比」類型所影響 (如果讀者忘了不同類型的對比是什麼，可回顧 ?sec-Different-ways-to-specify-contrasts 一節)。¹²

好啦，既然第三型分析所產出的 p 值，對「對比」的選擇如此敏感(這裡指jamovi以外的統計軟體)，這是否代表第三型檢定結果本質是武斷的、不可信的？某種程度上來說，確實如此；當我們稍後討論第二型的檢定策略，會看到第二型分析完全避免了這種武斷性。但本書作者認為這樣的判斷有些過於武斷。首先，務必認知到，某些「對比」的選擇，產出的答案永遠是相同 (啊，這就是 jamovi 的演算常態)。特別重要的一點是：若是對比矩陣的每一行總和都被限制為零，那麼第三型分析永遠都是提供相同的答案。

14.10.5 第二型平方和

好了，我們已經討論了第一型與第三型的假設檢定，兩種都相當直接了當。第一型是透過逐一加入模型效果項；第三型則是從完整模型出發，檢視移除每一個效果項後所發生的變化。然而，這兩種方式都有限制：第一型檢定會受到加入變項的順序影響；第三型檢定則會受到對比編碼方式的影響。相比之後，第二型的檢定雖然要用點功夫理解概念，但是能避免以上的問題，因此檢定結果的詮釋也相對容易。

第二型的檢定程序與第三型大致類似，都是從一個「完整」模型出發，透過刪除特定的項來進行檢定。不過，第二型是基於邊際性原則 (marginality principle)，這個原則主張：若模型中有高階效果項 (例如交互作用)，那麼所有與該高階效果相關的低階效果 (例如構成該交互作用的主要效果項) 都不應被省略。舉例來說，如果完整模型包括雙因子交互作用 A × B (二階效果項)，要比較的模型也應該要包括 A 與 B 這兩個主要效果 (一階效果項)。同理，如果完整模型包括三因子交互作用 A × B × C，要比較的模型就必須同時包含 A、B、C 三個主要效果，以及 A × B、A × C、B × C 等較簡單的交互作用。

第三型的檢定程序很容易違反邊際性原則。例如，處理包含所有可能交互作用項的三因子 ANOVA，根據第三型檢定，若要檢定 A 的主要效果，虛無假說與對立假說會是像 表 14.23 。

表 14.23:

在包含所有可能交互作用項的三因子 ANOVA 中，對主要效果 A 的第三型檢定

Null model:	\(outcome \sim B + C + A*B + A*C + B*C + A*B*C\)
Alternative model:	\(outcome \sim A + B + C + A*B + A*C + B*C + A*B*C\)

注意，這套虛無假說移除主要效果 A，卻有保留 A × B、A × C、以及 A × B × C 等項。根據第二型的觀點，這並不是一個好的虛無假說選擇。

若要檢定「A 與結果變項無關」的虛無假設，較好的做法應該是設定虛無假設為「不包含 A的任何最複雜模型形式，即使交互作用有A也不能算」；對立假設則是對應於這個虛無假設，再加上 A 的主要效果項。這個概念更貼近多數人對於「A 的主要效果」的直觀理解，所以第二型要檢定的模型組合如同 表 14.24 展示。¹³

表 14.24:

在包含所有可能交互作用項的三因子 ANOVA 中，對主要效果 A 的第二型檢定

Null model:	\(outcome \sim B + C + B*C\)
Alternative model:	\(outcome \sim A + B + C + B*C\)

總之，為了讓讀者對第二型的檢定過程有完整概念， 表 14.25 呈現一個三因子變異數分析，檢定各種效果項的假設模型。

表 14.25:

三因子模型的第二型檢定

Term being tested is	Null model is outcome ~ ...	Alternative model is outcome ~ ...
A	\(B + C + B*C \)	\(A + B + C + B*C \)
B	\(A + C + A*C \)	\(A + B + C + A*C\)
C	\(A + B + A*B \)	\(A + B + C + A*B\)
A*B	\(A + B + C + A*C + B*C \)	\(A + B + C + A*B + A*C + B*C \)
A*C	\(A + B + C + A*B + B*C \)	\(A + B + C + A*B + A*C + B*C \)
B*C	\(A + B + C + A*B + A*C \)	\(A + B + C + A*B + A*C + B*C \)
A*B*C	\(A + B + C + A*B + A*C + B*C \)	\(A + B + C + A*B + A*C + B*C + A*B*C \)

這個小節示範的 coffee 資料是個二因子設計，ANOVA 假設檢定更單純。主要效果「sugar」的 F 檢定，比較的是 表 14.26 展示的兩個模型。

表 14.26:

在 coffee 資料中，對「sugar」主要效果的第二型檢定

Null model:	\(babble \sim milk \)
Alternative model:	\(babble \sim sugar + milk\)

檢定「milk」主要效果，所比較的模型組合如 表 14.27 展示。

表 14.27:

在 coffee 資料中，對「milk」主要效果的第二型檢定

Null model:	\(babble \sim sugar \)
Alternative model:	\(babble \sim sugar + milk\)

最後，檢定「sugar × milk」交互作用的模型比較，請見 表 14.28 。

表 14.28:

對「sugar × milk」交互作用項的第二型檢定

Null model:	\(babble \sim sugar + milk \)
Alternative model:	\(babble \sim sugar + milk + sugar*milk \)

執行檢定的步驟同樣很簡潔：只要在 jamovi 的「ANOVA」–「模型 (Model)」的選單，將「平方和 (Sum of squares)」的選項改成「第二型 (Type 2)」，便能得到如同 圖 14.30 展示的 ANOVA 表格。

圖 14.30: 採用第二型平方和的 ANOVA 結果表格

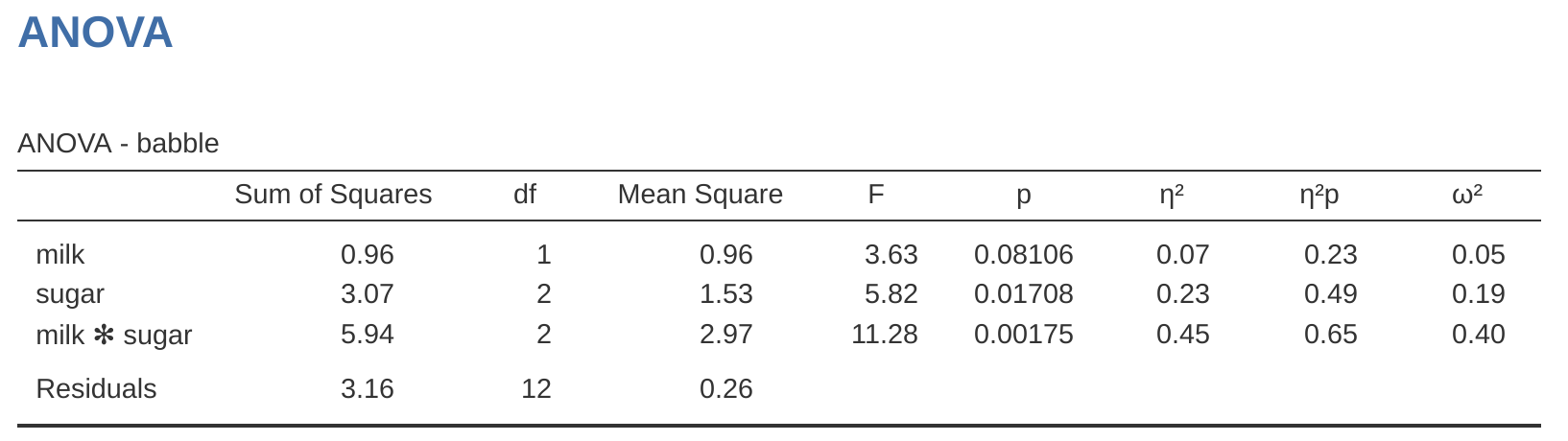
相較於第一型與第三型，第二型具有一些明顯的優勢：它既不依賴使用者指定因子的順序(第一型的缺點)，也不依賴使用者設定的對比編碼 (第三型的缺點)。 雖然關於對比編碼，學界尚未有清楚的共識，而且最終的選擇仍取決於研究者想要如何處理資料，但本書作者認為，第二型所檢定的假設，更有可能對應到研究者真正關心的問題。因此，詮釋第二型檢定的結果，通常會比詮釋第一型或第三型更容易。所以本書作者的初步建議是：若研究者想在不平衡設計中執行 ANOVA，卻又不清楚那些是能直接對應研究問題的模型比較組合，採用第二型檢定模式，可能是比第一型或第三型更好的選擇。¹⁴

14.10.6 效果量(還有非加成平方和)

如同 圖 14.30 展示的報表，選取計算效果量的選項，jamovi 會提供 \(\eta^2\) 與偏 \(\eta^2\) 等效果量估計值。然而，在不平衡設計中，這個課題會更複雜一些。

回顧一下先前有關 ANOVA 的討論，讀者應還記得從計算平方和學到的關鍵概念：將模型的所有效果項平方和 (SS) 與殘差平方和 (\(SS_R\)) 相加後，總和應等於總平方和 (\(SS_T\))。此外，\(\eta^2\) 的核心概念是，將某個效果項的 SS 除以總平方和，便能將 \(\eta^2\) 詮釋為該效果項所能解釋的變異量百分比。然而，在不平衡設計的狀況，事情就沒那麼單純了，因為部分的變異量會「憑空消失」。

第一次聽到這件事會覺得有點奇怪，原因說明如下：在不平衡的設計，因子之間會存在關聯性，導致我們很難區分因子 A 的效果與因子 B 的效果。最極端情況會像是 表 14.29 。

表 14.29:

2 × 2 極度不平衡因子設計中的 N 值

	sugar	no sugar
milk	100	0
no milk	0	100

在這個 \(2 \times 2\) 的實驗設計，各組人數極度不平衡：100 位受試者有牛奶也有糖，100 位受試者既無牛奶也無糖，然而，沒有任何受試者是「有牛奶、無糖」或「有糖、無牛奶」。現在假想一下，蒐集資料後發現，「有牛奶有糖」組與「無牛奶無糖」組之間，存在巨大且有統計顯著的差異。請問這是糖的主要效果？還是牛奶的主要效果？還是兩個變項的交互作用？我們完全無從得知，因為「有沒有糖」與「有沒有牛奶」兩者之間具有完全的關聯性。假如讓這個研究設計變得稍微平衡一些，像是 表 14.30 。

表 14.30:

仍然非常不平衡的 2 × 2 因子設計中的 N 值

	sugar	no sugar
milk	100	5
no milk	5	100

從技術上來說，這一次能夠區分牛奶與糖的效果了，因為總算有一些受試者只有牛奶或只有糖了。然而，區分兩個變項的效果依然相當困難，因為糖與牛奶之間仍然有非常強的關聯性，而且其中兩組的觀察值數量極少。我們很可能再次陷入一種情況：我們知道預測變項 (牛奶與糖) 與結果變項 (變得愛說話的程度) 有關，卻無法得知這些關聯性的本質，究竟是其中一個預測變項的主要效果，還是兩者的交互作用。

14.11 本章小結

• 平衡且無交互作用的因子設計分析以及[有交互作用因子設計分析]
• 因子設計變異數分析的效果量估計平均值以及信賴區間。
• [檢核變異數分析的執行條件]
• 共變數分析 (ANCOVA)
• 變異數分析就是線性模型還有各種多重比較方案
• 事後檢定談到杜凱氏HSD，還有提到規劃使用事前檢定方法要思考的條件。
• 不平衡的因子設計分析

Everitt, B. S. (1996). Making sense of statistics in psychology. A second-level course. Oxford University Press.

Hsu, J. C. (1996). Multiple comparisons: Theory and methods. Chapman; Hall.

---

1. 這套下標標示法的好處，在於其良好的延伸性 (generalisability)。如果我們的實驗包含第三個因子，只需多加一個下標即可。原則上，這套標示法可以延伸至任意數量的因子；但在本書中，我們罕少討論超過兩個因子的分析，且絕不涉及三個以上的因子。

2. 嚴格來說，邊際化 (marginalising) 與一般的平均數不完全相同。它是一種加權平均數 (weighted average)，計算時需考量所平均之不同事件的發生頻率。然而，在平衡設計 (balanced design) 中，根據定義，所有細格的次數 (cell frequencies) 皆相等，因此兩者是等價的。我們稍後會討論非平衡設計 (unbalanced designs)，屆時讀者將會發現，所有的計算都會變得相當棘手。但目前讓我們先忽略這個問題。

3. 現在我們的標示法已經確立，便可以用相對熟悉的方式，計算出兩個因子的平方和。對於因子 A，其組間平方和的計算，是透過衡量各個列的邊際平均數 (\(\bar{Y}_{1.}\)、\(\bar{Y}_{2.}\) 等) 與總平均數 (\(\bar{Y}_{..}\)) 之間的差異程度。計算方式與單因子變異數分析相同：計算 \(\bar{Y}_{r.}\) 值與 \(\bar{Y}_{..}\) 值之間的離均差平方和 (sum of squared difference)。具體來說，如果每個細格有 \(N\) 位受試者，那麼計算公式如下：
   \[SS_A=(N \times C)\sum_{r=1}^R (\bar{Y}_{r.}-\bar{Y}_{..})^2\]
   與單因子變異數分析一樣，此公式最不繁瑣[^a] 的部分，是 \((\bar{Y}_{r.}-\bar{Y}_{..})^2\) 這部分，它對應的是第 r 個水平的離均差平方。這個公式的運作方式是：先計算出因子所有 \(R\) 個水平的離均差平方，將其加總，最後再將結果乘以 \(N \times C\)。
   之所以要乘以 \(N \times C\)，是因為在我們的研究設計中，因子 A 的每一個水平 (如水平 \(r\)) 都會出現在多個細格裡。事實上，它會對應到因子 B 的所有 \(C\) 個水平，因此總共會出現在 \(C\) 個細格中。舉例來說，在我們的範例中，就有兩個不同的細格對應 Anxifree 這種藥物：一個是「無治療」組，另一個是「CBT」組。不僅如此，每一個細格中都還包含 \(N\) 個觀測值。因此，若我們想將這個平方和 (SS) 的計算基礎，轉換到「每一個觀測值」的層級，就必須乘以 \(N \times C\)。
   因子 B 的公式自然也是同理，只是更動了下標而已：
   \[SS_B=(N \times R)\sum_{c=1}^C (\bar{Y}_{.c}-\bar{Y}_{..})^2\]
   有了這些公式後，便可以將計算結果與先前章節的 jamovi 輸出進行核對。同樣地，建議讀者可使用試算表軟體來輔助這類計算，親自動手試試。讀者也可參考本書提供的 Excel 檔案 clinicaltrial_factorialanova.xls。
   首先，計算「藥物」主要效果的平方和。在每個細格中，受試者人數為 \(N = 3\)，而治療的種類 (因子 B 的水平數) 為 \(C = 2\)。換句話說，服用任一種特定藥物的總人數為 \(3 \times 2 = 6\) 人。在試算表軟體中完成計算後，會得到「藥物」主要效果的平方和為 3.45。不意外地，這個數值與 圖 14.3 的 ANOVA 表格中，「藥物」因子的 SS 值完全相同。
   接著，我們能以相同方式計算「治療」的效果。同樣地，每個細格的受試者人數為 \(N = 3\)，但這次藥物的種類 (因子 A 的水平數) 為 \(R = 3\)。因此，接受任一種特定治療的總人數為 \(3 \times 3 = 9\) 人。此次計算結果，會得到「治療」主要效果的平方和為 \(0.47\)。這個數值同樣也與 圖 14.3 的 ANOVA 輸出結果相符。
   以上就是計算兩個主要效果的平方和 (SS) 的方式。這些 SS 值，類似於我們在 單元 13 中進行單因子變異數分析時所計算的組間平方和。然而，最好不要再將它們視為組間平方和，因為現在有兩個不同的分組變項，容易造成混淆。
   不過，為了建構 F 檢定，我們還需要計算組內平方和 (within-groups sum of squares)。為了與 單元 12 章節及 jamovi 輸出的 ANOVA 表格術語保持一致，接下來會將組內平方和稱為殘差平方和 (\(SS_R\))。
   要理解殘差平方和，最簡單的方式，就是將其視為：在考量了邊際平均數的差異 (亦即減去 \(SS_A\) 與 \(SS_B\)) 之後，結果變項中所剩餘的變異量。也就是說，我們可以先計算出總平方和 (total sum of squares)，記為 \(SS_T\)。其計算公式與單因子變異數分析的公式幾乎相同：計算每一個觀測值 \(Y_{rci}\) 與總平均數 \(\bar{Y}_{..}\) 的離均差平方，再將全部數值加總。
   \[SS_T=\sum_{r=1}^R \sum_{c=1}^C \sum_{i=1}^N (Y_{rci}-\bar{Y}_{..})^2\]
   這裡的「三重加總 (triple summation)」看起來比實際上複雜。前兩個加總是對因子 A 的所有水平 (即表格中所有可能的行 r) 與因子 B 的所有水平 (即所有可能的列 c) 進行加總。每一個 rc 組合對應一個細格，而每個細格又包含 \(N\) 位受試者，因此我們還必須對細格中所有受試者 (即所有 \(i\) 值) 進行加總。換言之，我們在此所做的，就只是將資料集中的所有觀測值 (即所有可能的 rci 組合) 加總起來。
   至此，我們已知結果變項的總變異量 (\(SS_T\))，也知道其中有多少變異量可歸因於因子 A (\(SS_A\)) 及因子 B (\(SS_B\))。因此，殘差平方和的定義即為：無法歸因於這兩個因子的 Y 變異量。換言之：
   \[SS_R=SS_T-(SS_A+SS_B)\]
   當然，也可以使用一個公式來直接計算殘差平方和，但從概念上這樣思考會更有助於理解。之所以稱之為「殘差」，其意義便在於它是「剩餘的變異量」，而上述公式便清楚地體現了這點。此外也需注意，依照迴歸章節所使用的術語，通常會將 \(SS_A + SS_B\) 稱為可歸因於「ANOVA 模型」的模型平方和 (model sum of squares)，記為 \(SS_M\)。因此我們常說：總平方和等於模型平方和，加上殘差平方和。稍後在本章中將會看到，這不僅是表面上的相似：ANOVA 與迴歸在根本上其實是同一回事。
   無論如何，值得花點時間用此公式來計算 \(SS_R\)，並驗證我們得到的答案與 jamovi 的 ANOVA 表格輸出結果相同。在試算表軟體中，計算過程相當直接 (可參見 clinicaltrial_factorialanova.xls 檔案)：先用上述公式算出總平方和 (\(SS_T = 4.85\))，然後計算殘差平方和 (\(SS_R = 0.92\))。最終，我們再次得到了相同的答案。
   —
   [^a]：原文為 “least tedious”，意為「最不繁瑣」。

4. 要透過虛無假說與對立假說，將交互作用效應的概念公式化，確實有些困難，本書多數讀者對此可能也不會太感興趣。儘管如此，作者在此盡力為有興趣的讀者介紹其中的基本概念。
   首先，我們需要更明確地定義主要效果。以因子 A (本章範例資料的「藥物」) 的主要效果為例。我們最初是將其虛無假說定義為所有邊際平均數 (\(\mu_{r.}\)) 皆相等。顯然，若所有邊際平均數都相等，那它們必然也會等於總平均數 (\(\mu_{..}\))。因此，我們可以將因子 A 在水平 r 的效果 (effect) 定義為邊際平均數 \(\mu_{r.}\) 與總平均數 \(\mu_{..}\) 之間的差值。我們將此效果記為 \(\alpha_r\)，也就是：\[\alpha_r=\mu_{r.}-\mu_{..}\]根據定義，所有 \(\\alpha\_r\) 值的總和必然為零 (原因與「各列邊際平均數的平均值，必然等於總平均數」相同)。同理，我們也能定義因子 B 在水平 c 的效果，即行邊際平均數 \(\mu_{.c}\) 與總平均數 \(\mu_{..}\) 的差值：\[\beta_c=\mu_{.c}-\mu_{..}\]同樣地，所有 \(\beta_c\) 值的總和也必然為零。
   統計學家有時偏好使用 \(\alpha_r\) 與 \(\beta_c\) 這些參數來討論主要效果，是因為這能讓他們精確地定義「不存在交互作用」的意涵。如果完全沒有交互作用，那麼單靠 \(\alpha_r\) 與 \(\beta_c\) 這兩個主要效果參數，便足以完美地描述每一個細格平均數 (\(\mu_{rc}\))。具體來說，這代表：\[\mu_{rc}=\mu_{..}+\alpha_{r}+\beta_{c}\]換言之，只要知道所有的邊際平均數，就能完美預測出每一個細格平均數，不存在任何「特殊加成」。這，就是我們的虛無假說。而對立假說則是：在表格中，至少有一個細格 (\(rc\)) 的情況並非如此：\[\mu_{rc} \neq \mu_{..}+\alpha_{r}+\beta_{c}\]然而，統計學家們通常會偏好另一種稍微不同的寫法。他們會定義一個與細格 \(rc\) 相關的特定交互作用數值，並給它一個有點彆扭的稱呼：\((\alpha\beta)_{rc}\)。然後，他們會將對立假說寫成：\[\mu_{rc}=\mu_{..} +\alpha_{r} +\beta_{c} + (\alpha \beta )_{rc}\]其中，至少有一個細格的 \((\alpha\beta)_{rc}\) 不為零。這套標示法看起來有些不甚雅觀，但在後續討論平方和的計算時，讀者會發現這樣標示非常方便。
   那麼，交互作用項的平方和 (\(SS\_{A:B}\)) 該如何計算呢？首先，有助於我們回想先前是如何定義交互作用的：亦即「實際的細格平均數」與「僅從邊際平均數推斷的預期值」之間的差異程度。當然，先前所有的公式都涉及母群參數而非樣本統計量，所以我們無從得知其真實數值。然而，我們可以透過樣本平均數來取代母群平均數，藉此估計這些參數。
   因此，對於因子 A，其在水平 r 的主要效果，一個好的效果估計值( \(\hat{\alpha}_r\)) 便是在樣本中所觀察到的邊際平均數 \(\bar{Y}_{r.}\) 與總平均數 \(\bar{Y}_{..}\) 的差值：\[\hat{\alpha}_r = \bar{Y}_{r.}-\bar{Y}_{..}\]同理，因子 B 在水平 c 的主要效果的估計值 (\(\hat{\beta}_c\)) 則為： \[\hat{\beta}_{c}=\bar{Y}_{.c}-\bar{Y}_{..}\] 若讀者回顧前文用來描述兩個主要效果的 SS 公式，便會注意到，這些「效果估計值」(\(\hat{\alpha}_r\) 與 \(\hat{\beta}_c\)) 正是我們進行平方與加總的對象！那麼，這個邏輯該如何類比到交互作用項上呢？答案可以透過重新排列對立假說的公式來得到： \[\begin{aligned} (\alpha \beta)_{rc} & = \mu_{rc} - \mu_{..} - \alpha_r - \beta_c \\ & = \mu_{rc} - \mu_{..} - (\mu_{r.}-\mu_{..})-(\mu_{.c}-\mu_{..}) \\ & = \mu_{rc} - \mu_{r.} - \mu_{.c} +\mu_{..} \end{aligned}\] 如此一來，只要再次以樣本統計量取代母群平均數，我們便能得到細格 \(rc\) 的交互作用效果估計值，亦即：\[(\hat{\alpha \beta})_{rc}=\bar{Y}_{rc}-\bar{Y}_{r.}-\bar{Y}_{.c}+\bar{Y}_{..}\] 現在，我們只需將所有細格的交互作用效果估計值，對因子 A 的所有 \(R\) 個水平、以及因子 B 的所有 \(C\) 個水平進行加總，便能得到整個交互作用的平方和公式：
   \[SS_{A:B}=N \sum_{r=1}^R \sum_{c=1}^C (\bar{Y}_{rc}-\bar{Y}_{r.}-\bar{Y}_{.c}+\bar{Y}_{..})^2\] 此處之所以要乘以 \(N\)，是因為每個細格中都有 \(N\) 個觀測值，而我們希望 SS 值所反映的，是由交互作用所解釋的「觀測值之間」的變異，而非「細格之間」的變異。
   有了計算 \(SS_{A:B}\) 的公式後，務必認知到交互作用項也是模型的一部分。因此，與模型相關的平方和 (\(SS_M\))，現在會等於三個相關平方和的總和：\(SS_A + SS_B + SS_{A:B}\)。
   殘差平方和 (\(SS_R\)) 的定義依然是剩餘的變異量，即 \(SS_T - SS_M\)；但由於現在模型中包含了交互作用項，其公式變為：\[SS_R=SS_T-(SS_A+SS_B+SS_{A:B})\]這麼做的結果是，此處的殘差平方和 (\(SS_R\))，將會小於我們原先那個不包含交互作用項的 ANOVA 模型中的殘差平方和。

5. 前一節我們討論如何查看jamovi報表的主要效果分析時，讀者可能已經發現這一點。為讓本書的解釋脈絡順暢，前一節呈現的模型特意刪除交互作用項，以保持內容清晰簡單。

6. 這個單元似乎創下了字母 R 指涉對象數量的新紀錄。到目前為止，R 已經代表過：R 語言套件、平均數表格的列數 (rows)、模型中的殘差 (residuals)，以及現在迴歸分析中的相關係數 (correlation coefficient)。向各位說聲抱歉，英文字母顯然不夠用。不過，本書已經盡力在內文中清楚標示每個 R 的不同指涉對象。

7. 讀者可能會好奇，處置對比與簡易對比之間有何差異？以一個性別為主要效果案例來說，假設男性 (m) 編碼為 0，女性 (f) 編碼為 1。在處置對比中，迴歸係數所衡量的，是女性與男性平均數之間的差異，而截距項則會是男性的平均數 (基準組)。然而，若採用簡易對比 (例如將男性編碼為 -1，女性為 1)，截距項則是兩組平均數的平均值，也就是總平均數。主要效果參數所代表的，就是各組平均數與此截距項的差異值。

8. 舉例來說，若研究者想知道的是「A 組的平均數，是否與 B、C 兩組的平均值顯著不同」，那麼就需要使用不同的工具 (例如更為保守的 Scheffe 法，這也超出了本書範圍)。然而，在多數統計實務，研究者關心的通常是成對的組間差異，因此 Tukey’s HSD 是相當實用的工具。

9. 各組標準差的差異，可能會讓細心的讀者懷疑，這些資料是否違反變異數同質性的適用條件？本書將此問題當作練習題，讓讀者自行使用 Levene 檢定做檢核。

10. 坦白說，這裡的說法並不完全正確。除了本書所討論的類型之外，ANOVA模型還有其他的變化形式。例如，本書完全不談固定效果模型 (fixed-effect models) (因子的水準由實驗者或資料世界所「固定」) 與隨機效果模型 (random-effect models) (因子的水準是從一個更大的可能水準母群中隨機抽樣而來) 之間的差異，本書只討論固定效果模型。讀者切勿誤以為本書或任何一本書，能告訴你所有「你需要知道的統計學知識」，如同不可能有一本書可以窮盡所有心理學、物理學或哲學的知識一樣。現實世界遠比任何一本書複雜得多。不過，讀者不必感到絕望。多數研究者僅憑藉本書所涵蓋的 ANOVA 基礎知識，便足以應付研究工作。這裡只是想提醒讀者，本書只是一個漫長故事的開端，而非全部。

11. 或至少可以說，是很少能引發研究興趣的。

12. 然而，無論使用者選擇何種對比， jamovi 的第三型平方和 ANOVA 分析結果都是相同的。因此，jamovi 顯然採用某些不一樣的運算方式！

13. 當然，要如何設定取決於使用者所設定的原始模型。若原始模型並未有 B × C 的交互作用，那麼虛無或對立假設自然也不會有這一項。但這點對三種類型的檢定程序來說都一樣：統計軟體演算法永遠不會納入使用者未曾指定的效果項，演算法只會針對使用者已納入的項，提供不同的檢定模型建構。

14. 有趣的是，R語言的預設是第一型，SPSS 與 jamovi 的預設卻是第三型。這兩種設定都不甚合我意。此外，更令人沮喪的是，心理學文獻中幾乎沒有人會費心報告他們究竟用了哪一種類型的檢定，更不用說報告第一型的變項順序、或第三型的對比類型了。他們通常連自己用了什麼軟體也不報告。唯一能理解這些報告的方式，就是從字裡行間透露的蛛絲馬跡去猜測他們用了哪套軟體，並假設他們從未更改過任何預設值。請千萬不要這麼做！已經了解這些議題的讀者，請務必在報告中註明你所使用的軟體型號；如果報告的資料是用不平衡設計的 ANOVA 結果，請指明你執行的是哪一種類型的檢定；若是第一型，請註明變項順序；若是第三型，請註明對比類型。或者，更好的做法是：直接針對那些能對應你真正關心議題的假說檢定，然後如實報告它們！