12 比較多組平均值(單因子變異數分析)
譯者註 20230416初步以ChatGPT-4完成翻譯,內容待編修。
本章介紹了心理統計學中最廣泛使用的工具之一,稱為”變異數分析”,但通常簡稱為ANOVA。基本程序來自20世紀初的羅蘭.費雪爵士的貢獻,他給這套方法的命名也給此時此刻正在學習與使用這套方法的我們一些苦惱。變異數分析這個名稱通常會帶給初學者兩點誤導。首先,儘管名字裡有「變異數」,實際上ANOVA是比較平均數之間的差異。其次,有好幾套統計方法都與變異數分析有密切關係,其中一些方法的名稱只與其命名有非常微弱的聯繫。在後續章節,我們會學到各式各樣的變異數分析方法,分別有各自適用的情況,但就本章的學習目的而言,我們只會學習最簡單的單因子變異數分析,即研究設計只有觀察幾個不同群組,我們的興趣是了解這些群組在某個獨變項的測量結果是否有所不同。
本章的學習順序如下:首先,我將介紹示範用的虛擬資料集,在這一章會使用這個資料集進行操作示範。接著我將說明單因子變異數分析的運作原理,然後詳細說明如何使用 jamovi的變異數分析模組執行變異數分析。這兩個部分是本章重點。
接下來分別討論在執行變異數分析時必須考慮的一系列重要課題,像是如何計算效果量大小、事後檢定和多重比較的校正,以及變異數分析的適用條件。我們還會討論如何檢查這些條件,以及適用條件不成立時可以做什麼樣的補救措施。最後一節,我們會學習重覆量數變數分析。
12.1 獨立樣本變異數分析示範資料
假想你協助執行一件臨床試驗,研究一種名為Joyzepam的新型抗憂鬱藥物效用。為了公平地測試這種新藥的效用,你要分別測試包括新藥的三種藥物。另外兩種的其中一種是安慰劑,另一種是已經上市,名為Anxifree的抗憂鬱/抗焦慮藥物。你一開始招募了18名患有中度至重度抑鬱症的參與者。由於有的參與者不只有服用藥物,也同時接受心理治療,因此所有參與者包括9個正在進行認知行為治療(CBT)的個案和9個未進行任何治療的個案。參與者以雙盲的隨機方式派給藥物,因此每一種藥物分給3位接受CBT的個案和3位無接受治療的個案。每位個案各自使用被分派的藥物3個月後,再由研究者評估每個人的情緒改善狀態,從\(-5\)到\(+5\)的範圍代表每位個案的情緒改善狀況。現在我們可以載入資料檔 clinicaltrial.csv,看看這種研究設計的內容,檔案包含三個變項,分別是藥物、治療和情緒提升分數。
以這一章的學習目標來說,我們想了解的是藥物對情緒提升的效用。首先要做的是進行描述性統計並繪製一些圖表。在 Chapter 4 ,同學們已經學到如何使用完成描述統計,就像 Figure 12.1 顯示的圖表。
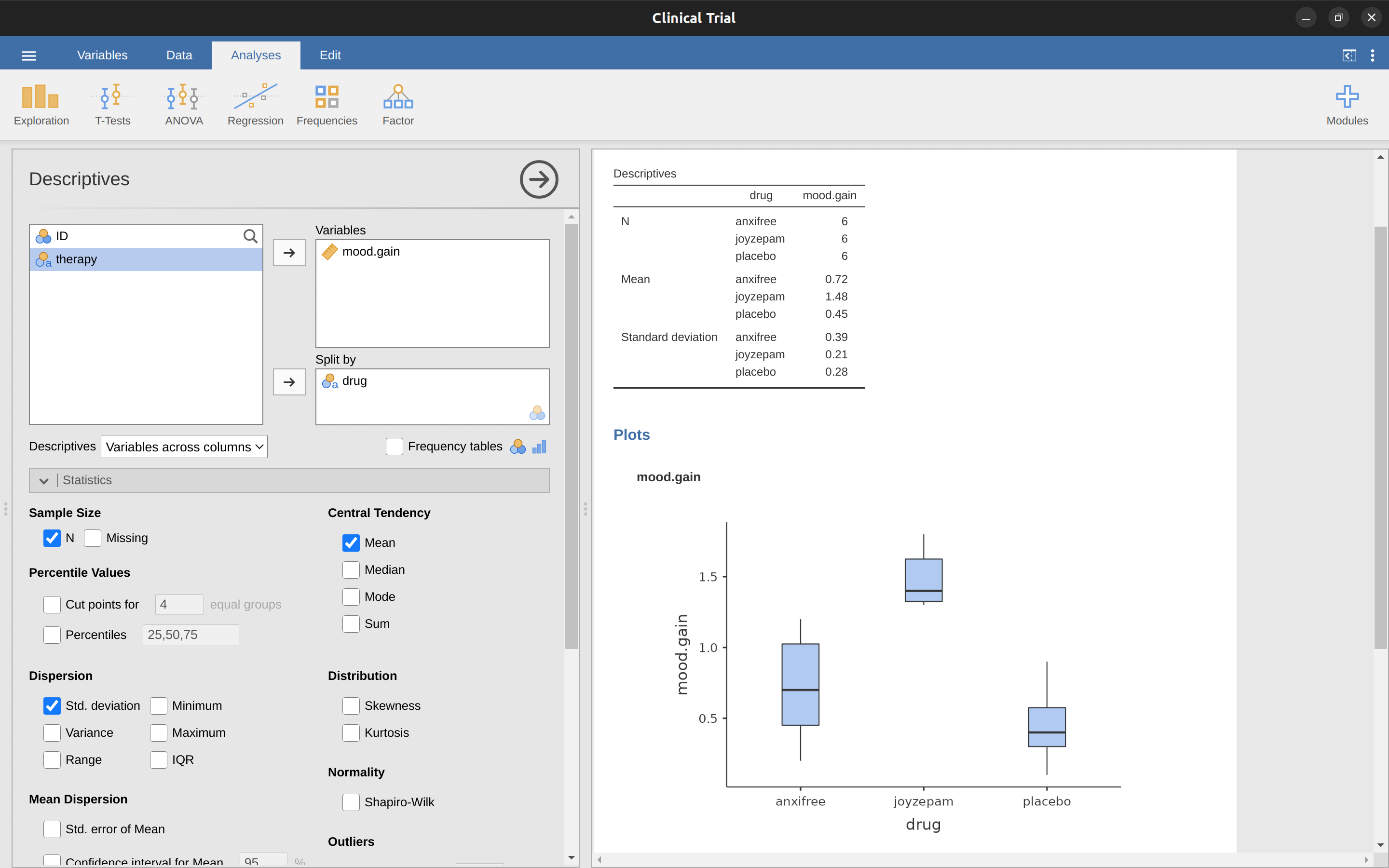
如 Figure 12.1 所示,服用Joyzepam的參與者,情緒的改善程度大於服用Anxifree或安慰劑。Anxifree的情緒提升程度大於安慰劑,但是差距沒有像Joyzepam那麼大。在此要回答的問題是,這些藥效的差異是否“真有其事”,還是僅僅是偶然的結果?
12.2 變異數分析的運作原理
為了回答我們的臨床試驗數據所提出的問題,我們將進行單因素變異數分析(one-way ANOVA)。首先,我將通過自下而上地構建統計工具並向您展示,如果您無法使用jamovi中的任何酷炫內置ANOVA功能,該如何做。我希望您能仔細閱讀,嘗試一兩次用較長的方法來確保您真正了解ANOVA是如何運作的,然後一旦您掌握了概念,就永遠不要再用這種方法了。
在上一節中我描述的實驗設計強烈表明,我們對比較三種不同藥物的平均心情變化感興趣。在這個意義上,我們討論的分析類似於t檢驗(參見 Chapter 11 ),但涉及多於兩個組別。如果我們讓\(\mu_P\)表示安慰劑引起的情緒變化的母體平均值,並讓\(\mu_A\)和\(\mu_J\)表示我們的兩種藥物Anxifree和Joyzepam的對應平均值,那麼我們要檢驗的(有些悲觀的)虛無假設是:所有三個母體平均值都相同。也就是說,這兩種藥物都沒有比安慰劑更有效。我們可以將此虛無假設寫為:
\[H_0: \text{ 事實上 } \mu_P=\mu_A=\mu_J\]
因此,我們的替代假設是:三種不同治療中至少有一種與其他治療不同。將其用數學表示有點困難,因為(正如我們將要討論的那樣)虛無假設可能以很多不同的方式是錯誤的。所以目前我們只將替代假設寫成這樣:
\[H_1: \text{ 事實 }\underline{ 不是 }\text{ } \mu_P=\mu_A=\mu_J\]
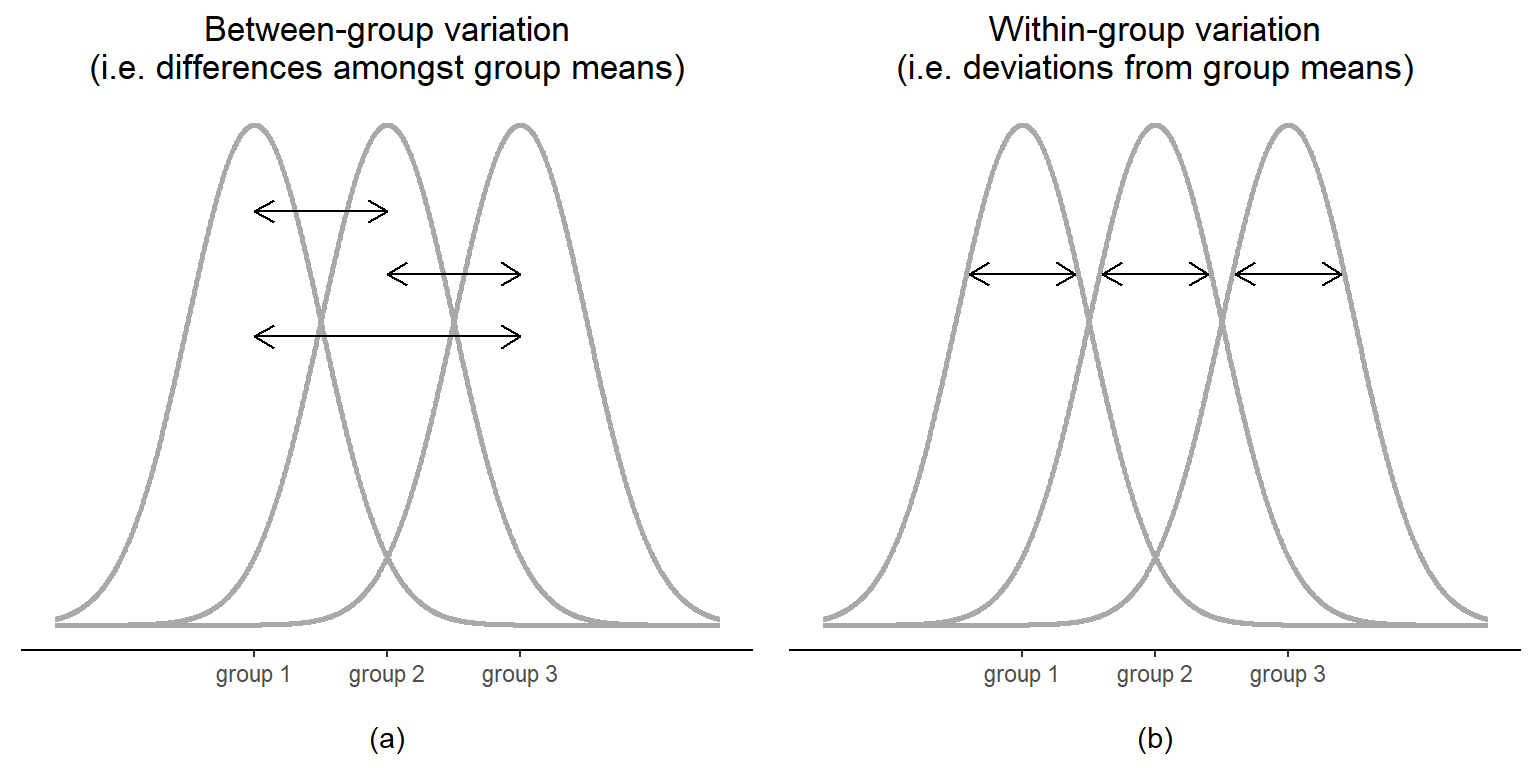
這個虛無假設比我們之前見過的任何一個都要棘手得多。我們應該如何檢驗它?一個明智的猜測是「進行方差分析」,因為這是本章的標題,但是目前還不太清楚為什麼「方差分析」會幫助我們了解有關均值的有用信息。事實上,這是人們首次接觸方差分析時遇到的最大概念困難之一。要了解其原理,我認為從方差開始談起是最有幫助的,具體來說就是組間變異性和組內變異性( Figure 12.2 )。
12.2.1 計算依變項變異數的兩套公式
首先,讓我們引入一些符號。我們將使用 G 來表示組的總數。對於我們的數據集,有三種藥物,所以有 \(G = 3\) 個組。接下來,我們將使用 \(N\) 表示總樣本大小;在我們的數據集中,一共有 \(N = 18\) 人。同樣地,讓我們用 \(N_k\) 表示第 k 個組中的人數。在我們的虛擬臨床試驗中,所有三組的樣本大小都是 \(N_k = 6\)。1 最後,我們將使用 Y 表示結果變項。在我們的案例中,Y 指的是心情變化。具體來說,我們將使用 Yik 指代第 k 個組中第 i 個成員所經歷的心情變化。同樣,我們將使用 \(\bar{Y}\) 作為實驗中所有 18 人的平均心情變化,並使用 \(\bar{Y}_k\) 指代第 k 組中 6 人所經歷的平均心情變化。
現在我們已經整理好符號,我們可以開始寫下公式。首先,讓我們回想一下在 Section 4.2 中使用的方差公式,在那個做描述性統計的較早時期。Y 的樣本方差被定義為以下公式 \[Var(Y)=\frac{1}{N}\sum_{k=1}^{G}\sum_{i=1}^{N_k}(Y_{ik}-\bar{Y})^2\] 這個公式看起來與 Section 4.2 中的方差公式幾乎相同。唯一的區別是這次我有兩個求和:我對組進行求和(即 \(k\) 的值)以及對組內的人進行求和(即 \(i\) 的值)。這只是一個純粹的表面細節。如果我使用符號 \(Y_p\) 來表示樣本中第 p 個人的結果變項值,那麼我只有一個求和。我們在這裡有兩個求和的唯一原因是我將人分類到組,然後為組內的人分配數字。
在這裡,具體的例子可能很有用。讓我們考慮 Table 12.1 ,在這個表格中,我們有總共 \(N = 5\) 個人分成 \(G = 2\) 個組。任意地說,讓我們說「酷」的人是第 1 組,「不酷」的人是第 2 組。結果發現我們有三個酷人(\(N_1 = 3\))和兩個不酷的人(\(N_2 = 2\))。
| name | person P | group | group num. k | index in group | grumpiness \( Y_{ik} \) or \( Y_p \) |
|---|---|---|---|---|---|
| Ann | 1 | cool | 1 | 1 | 20 |
| Ben | 2 | cool | 1 | 2 | 55 |
| Cat | 3 | cool | 1 | 3 | 21 |
| Tim | 4 | uncool | 2 | 1 | 91 |
| Egg | 5 | uncool | 2 | 2 | 22 |
注意到這裡我構建了兩個不同的標記方案。我們有一個「人」變項 p,所以說到 Yp 作為樣本中的第 p 人的脾氣是完全合理的。例如,表格顯示 Tim 是第四個,所以我們會說 \(p = 4\)。所以,在談到這個「Tim」這個人(無論他是誰)的脾氣 \(Y\) 時,我們可以通過說 \(Y_p = 91\) 來指稱他的脾氣,即對於人 \(p = 4\)。然而,這不是我們唯一可以指稱 Tim 的方法。作為一個替代方法,我們可以注意到 Tim 屬於「不酷」的組(\(k = 2\)),實際上是不酷組中列出的第一個人(\(i = 1\))。所以,通過說 \(Y_{ik} = 91\),在 \(k = 2\) 和 \(i = 1\) 的情況下,同樣有效地指稱 Tim 的脾氣。
換句話說,每個人 p 都對應一個唯一的 ik 組合,所以我之前給出的公式實際上與我們原始的方差公式是相同的,即 \[Var(Y)=\frac{1}{N}\sum_{p=1}^{N}(Y_p-\bar{Y})^2\] 在兩個公式中,我們所做的就是對樣本中的所有觀察值求和。大多數時候,我們只使用更簡單的 Yp 記號;使用 \(Y_p\) 的等式顯然是兩者中更簡單的一個。然而,在進行方差分析(ANOVA)時,我們需要跟踪哪些參與者屬於哪個組別,並且我們需要使用 Yik 記號來完成這項工作。
12.2.2 變異數與平方差總和
好的,既然我們對方差的計算有了很好的了解,讓我們定義一個叫做總平方和(total sum of squares)的東西,記作 SStot。這很簡單。計算方差時,我們是對平方偏差求平均,而計算總平方和時,我們只需將它們加起來。2
當我們在 ANOVA 的上下文中談論分析變異數時,我們實際上是在處理總平方和,而不是實際的方差。3
接下來,我們可以定義一個僅捕捉組間差異的變異概念。我們通過查看組平均值 \(\bar{Y}_k\) 和整體平均值 \(\bar{Y}\) 之間的差異來實現這一點。4
這並不太難以證明,實驗中人們之間的總變異(\(SS_{tot}\))實際上是組間差異(\(SS_b\))和組內變異(\(SS_w\))之和。即,
\[SS_w+SS_b=SS_{tot}\] 好耶。
好的,那麼我們發現了什麼?我們已經發現了與結果變項相關的總變異(\(SS_{tot}\))可以在數學上被劃分為“由於不同組的樣本均值之間的差異所產生的變異”(\(SS_b\))加上“其他所有變異”(\(SS_w\))之和5。
那怎麼幫助我找出這些組是否有不同的母體均值呢?嗯。等等。稍等一下。現在想想,這正是我們在尋找的。如果原假設成立,那麼您會期望所有樣本均值彼此非常相似,對吧?這將意味著您會期望 \(SS_b\) 非常小,或者至少您會期望它比“與其他所有事物相關的變異”(\(SS_w\))小得多。嗯。我感覺到了一個假設檢驗的來臨。
12.2.3 平方差總和與F檢定
正如我們在上一節中看到的,ANOVA 的定性思想是將兩個平方和值 \(SS_b\) 和 \(SS_w\) 相互比較。如果組間變異 \(SS_b\) 相對於組內變異 \(SS_w\) 較大,那麼我們有理由懷疑不同組的母體均值彼此並不相同。為了將這一點轉化為可操作的假設檢驗,我們需要進行一些“小小的調整”。首先,我將向您展示我們如何計算檢驗統計量——F 值(F ratio),然後嘗試讓您了解為什麼我們要這樣做。
為了將我們的 SS 值轉換為 F 比,我們首先需要計算與 \(SS_b\) 和 \(SS_w\) 值相關的自由度。通常情況下,自由度對應於對特定計算做出貢獻的唯一“數據點”的數量,減去它們需要滿足的“約束”條件的數量。對於組內變異性,我們計算的是個體觀測值(\(N\) 個數據點)與組平均值(\(G\) 個約束)之間的變異。相反,對於組間變異性,我們關心的是組平均值(\(G\) 個數據點)在整體平均值(1 個約束)周圍的變化。因此,在這裡的自由度為:
\[df_b=G-1\] \[df_w=N-G\]
好吧,這似乎很簡單。接下來,我們將平方和值轉換為“平均平方”值,方法是除以自由度:
\[MS_b=\frac{SS_b}{df_b}\] \[MS_w=\frac{SS_w}{df_w}\]
最後,我們通過將組間 MS 除以組內 MS 來計算 F 比:
\[F=\frac{MS_b}{MS_w}\]
從非常一般的層面上,F 統計量背後的直覺很簡單。F 值越大,表示組間變異相對於組內變異越大。因此,F 值越大,我們反駁虛無假設的證據就越多。但是 \(F\) 必須多大才能實際拒絕 \(H_0\)?要理解這一點,您需要更深入地了解 ANOVA 是什麼以及平均平方值實際上是什麼。
下一節將詳細討論這個問題,但對於不感興趣實際衡量試驗內容的讀者,我將直接進入主題。為了完成我們的假設檢定,我們需要知道在虛無假設為真時 F 的抽樣分佈。不足為奇的是,在虛無假設下 F 統計量的抽樣分佈是一個 \(F\) 分佈。如果您回顧我們在 Chapter 7 中關於 F 分佈的討論,\(F\) 分佈有兩個參數,對應於涉及的兩個自由度。第一個 \(df_1\) 是組間自由度 \(df_b\),第二個 \(df_2\) 是組內自由度 \(df_w\)。
| between
groups | within
groups | |
|---|---|---|
| df | \( df_b=G-1 \) | \( df_w=N-G \) |
| sum of squares | \( SS_b=\sum_{k=1}^{G} N_k (\bar{Y}_k-\bar{Y})^2 \) | \( SS_w=\sum_{k=1}^{G} \sum_{i=1}^{N_k} (Y_{ik}-\bar{Y}_k)^2 \) |
| mean squares | \( MS_b=\frac{SS_b}{df_b} \) | \( MS_w=\frac{SS_w}{df_w} \) |
| F-statistic | \( F=\frac{MS_b}{MS_w} \) | - |
| p-value | [complicated] | - |
在 Table 12.2 中顯示了涉及單因素 ANOVA 的所有關鍵數量的概要,包括顯示如何計算它們的公式。
[額外的技術細節 6]
12.2.4 實例演練
先前的討論相當抽象且有點技術性,所以我認為此刻可能需要看一個實際示例。為此,讓我們回到本章開頭介紹的臨床試驗數據。我們在開始時計算的描述性統計數據告訴我們各組的平均值:安慰劑的平均情緒增益為 \(0.45\),Anxifree 為 \(0.72\),Joyzepam 為 \(1.48\)。有了這個想法,讓我們像 1899 年一樣開趴7,開始用鉛筆和紙做一些計算。我只會對前 \(5\) 個觀察值進行此操作,因為現在不是該死的 \(1899\) 年,而且我非常懶。讓我們從計算 \(SS_w\) 開始,即組內平方和。首先,讓我們繪製一個漂亮的表格來協助我們的計算( Table 12.3 )
| group k | outcome \( Y_{ik} \) |
|---|---|
| placebo | 0.5 |
| placebo | 0.3 |
| placebo | 0.1 |
| anxifree | 0.6 |
| anxifree | 0.4 |
在這個階段,我在表格中包含的只是原始數據本身。也就是說,每個人的分組變項(即藥物)和結果變項(即心情增益)。請注意,這裡的結果變項對應於我們先前方程式中的 \(\bar{Y}_{ik}\) 值。接下來的計算步驟是為研究中的每個人寫下相應的組平均值,\(\bar{Y}_k\)。這有點重複,但並不是特別困難,因為我們在進行描述性統計時已經計算了這些組平均值,見 Table 12.4 。
| group k | outcome \( Y_{ik} \) | group mean \( \bar{Y}_k \) |
|---|---|---|
| placebo | 0.5 | 0.45 |
| placebo | 0.3 | 0.45 |
| placebo | 0.1 | 0.45 |
| anxifree | 0.6 | 0.72 |
| anxifree | 0.4 | 0.72 |
既然我們已經寫下了這些,我們需要再次為每個人計算與相應組平均值的偏差。也就是說,我們想要減去 \(Y_{ik} - \bar{Y}_k\)。在我們做完這個之後,我們需要將所有東西平方。當我們這樣做時,這就是我們得到的結果( Table 12.5 )
| group k | outcome \( Y_{ik} \) | group mean \( \bar{Y}_k \) | dev. from group mean \( Y_{ik} - \bar{Y}_k \) | squared deviation \( (Y_{ik}-\bar{Y}_k)^2 \) |
|---|---|---|---|---|
| placebo | 0.5 | 0.45 | 0.05 | 0.0025 |
| placebo | 0.3 | 0.45 | -0.15 | 0.0225 |
| placebo | 0.1 | 0.45 | -0.35 | 0.1225 |
| anxifree | 0.6 | 0.72 | -0.12 | 0.0136 |
| anxifree | 0.4 | 0.72 | -0.32 | 0.1003 |
最後一步同樣簡單。為了計算組內平方和,我們只需將所有觀察值的平方偏差相加:
\[ \begin{split} SS_w & = 0.0025 + 0.0225 + 0.1225 + 0.0136 + 0.1003 \\ & = 0.2614 \end{split} \]
當然,如果我們真的想得到正確的答案,我們需要對數據集中的所有18個觀察值進行此操作,而不僅僅是前五個。如果我們想要的話,我們可以繼續使用鉛筆和紙進行計算,但這相當繁瑣。或者,使用專用的電子表格程序(如 OpenOffice 或 Excel)也不是很困難。嘗試自己做。我在 Excel 中做的那個文件名為 clinicaltrial_anova.xls。當你做完後,你應該得到一個組內平方和值為 \(1.39\)。
好的。現在我們已經計算了組內變異 \(SS_w\),是時候將我們的注意力轉向組間平方和 \(SS_b\) 了。對於這種情況,計算非常相似。主要區別在於,對於所有觀察值,我們不再計算觀察值 Yik 和組平均值 \(\bar{Y}_k\) 之間的差異,而是計算所有組的組平均值 \(\bar{Y}_k\) 和總平均值 \(\bar{Y}\)(在這種情況下為 \(0.88\))之間的差異(Table 12.6)。
| group k | group mean \( \bar{Y}_k \) | grand mean \( \bar{Y} \) | deviation \( \bar{Y}_k - \bar{Y} \) | squared deviation \( ( \bar{Y}_k-\bar{Y})^2 \) |
|---|---|---|---|---|
| placebo | 0.45 | 0.88 | -0.43 | 0.19 |
| anxifree | 0.72 | 0.88 | -0.16 | 0.03 |
| joyzepam | 1.48 | 0.88 | 0.60 | 0.36 |
然而,對於組間計算,我們需要將每個平方偏差乘以 \(N_k\),即組中的觀察值數量。我們這樣做是因為該組中的每個觀察值(所有 \(N_k\) 個觀察值)都與組間差異有關。因此,如果安慰劑組有六個人,並且安慰劑組的平均值與總平均值相差 \(0.19\),那麼這六個人與組間變異之間的關聯總和為 \(6 \times 0.19 = 1.14\)。因此,我們必須擴展我們的計算表格( Table 12.7 )。
| group k | ... | squared deviations \( (\bar{Y}_k-\bar{Y})^2 \) | sample size \( N_k \) | weighted squared dev \( N_k (\bar{Y}_k-\bar{Y})^2 \) |
|---|---|---|---|---|
| placebo | ... | 0.19 | 6 | 1.14 |
| anxifree | ... | 0.03 | 6 | 0.18 |
| joyzepam | ... | 0.36 | 6 | 2.16 |
現在,我們的組間平方和是通過將這些“加權平方偏差”在研究中的所有三組中求和而得到的:
\[\begin{aligned} SS_b & = 1.14 + 0.18 + 2.16 \\ &= 3.48 \end{aligned}\]
如您所見,組間計算要短得多 8。現在我們已經計算出了平方和值 \(SS_b\) 和 \(SS_w\),剩下的 ANOVA 分析就相當簡單了。下一步是計算自由度。由於我們有 \(G = 3\) 個組和 \(N = 18\) 個觀察值,我們的自由度可以通過簡單的減法來計算:
\[ \begin{split} df_b & = G-1 = 2 \\ df_w & = N-G = 15 \end{split} \]
接下來,由於我們已經計算了平方和值和自由度的值,對於組內變異性和組間變異性,我們可以通過將一個除以另一個來獲得平均平方值:
\[ \begin{split} MS_b & = \frac{SS_b}{df_b} = \frac{3.48}{2} = 1.74 \\ MS_w & = \frac{SS_w}{df_w} = \frac{1.39}{15} = 0.09 \end{split} \]
我們快完成了。平均平方值可用於計算我們感興趣的 F 值,這是我們感興趣的檢驗統計量。我們通過將組間 MS 值除以組內 MS 值來完成此操作。
\[ \begin{split} F & = \frac{MS_b}{MS_w} = \frac{1.74}{0.09} \\ & = 19.3 \end{split} \]
哇!這真的非常令人興奮,對嗎?現在我們有了檢驗統計量,最後一步是找出檢驗本身是否給我們一個顯著結果。如 Chapter 9 在“過去的日子”中所討論的,我們要做的是打開一本統計教科書或翻到後面的部分,這裡會有一個巨大的查找表,我們會找到對應特定 alpha 值(空假設拒絕區域)的閾值 F 值,例如 \(0.05\),\(0.01\) 或 \(0.001\),對於 2 和 15 度的自由度。用這種方法,對於 alpha 為 \(0.001\) 的情況,我們會得到一個閾值 F 值為 \(11.34\)。由於這小於我們計算出的 F 值,我們說 \(p < 0.001\)。但那是過去的日子,現在花哨的統計軟件會為您計算出確切的 p 值。實際上,確切的 p 值為 \(0.000071\)。所以,除非我們對 Type I 錯誤率非常保守,否則我們幾乎可以保證拒絕虛無假設。
此刻,我們基本上完成了。完成計算後,將所有這些數字整理成類似於表 12.1 的 ANOVA 表是傳統做法。對於我們的臨床試驗數據,ANOVA 表將如 Table 12.8 。
| df | sum of squares | mean squares | F-statistic | p-value | |
|---|---|---|---|---|---|
| between groups | 2 | 3.48 | 1.74 | 19.3 | 0.000071 |
| within groups | 15 | 1.39 | 0.09 | - | - |
如今,您可能永遠沒有太多理由想要自己構建這樣的表格,但您會發現幾乎所有的統計軟件(包括 jamovi)都傾向於將 ANOVA 的輸出組織成這樣的表格,所以最好習慣閱讀它們。然而,儘管軟件將輸出完整的 ANOVA 表,但幾乎從來沒有充分理由在您的撰寫中包含整個表格。報告此結果的統計塊的一種非常標準的方法是寫下類似以下的內容:
單因素 ANOVA 顯示藥物對情緒增益有顯著影響(F(2,15) = 19.3,p < .001)。
嘆氣。這麼多工作,只為了一個簡短的句子。
12.3 jamovi的變異數分析模組
我相當確定在讀完上一節之後,您在想什麼,特別是如果您按照我的建議,用鉛筆和紙(即在試算表中)自己完成所有這些工作。自己做 ANOVA 計算很糟糕。沿途我們需要做相當多的計算,如果每次想做 ANOVA 都要一次又一次地做這些計算,會讓人厭煩。
12.3.1 使用jamovi完成變異數分析
為了讓您的生活更輕鬆,jamovi 可以做 ANOVA… 哈拉! 轉到「ANOVA」-「ANOVA」分析,將 mood.gain 變項移到「依賴變項」框中,然後將 drug 變項移到「固定因子」框中。這樣應該會得到 Figure 12.3 中所示的結果。9 注意我還勾選了 ’Effect Size’選項下的 \(\eta^2\) 复选框,念作“ eta 平方”,這也顯示在結果表格上。稍後我們將回到效應大小。
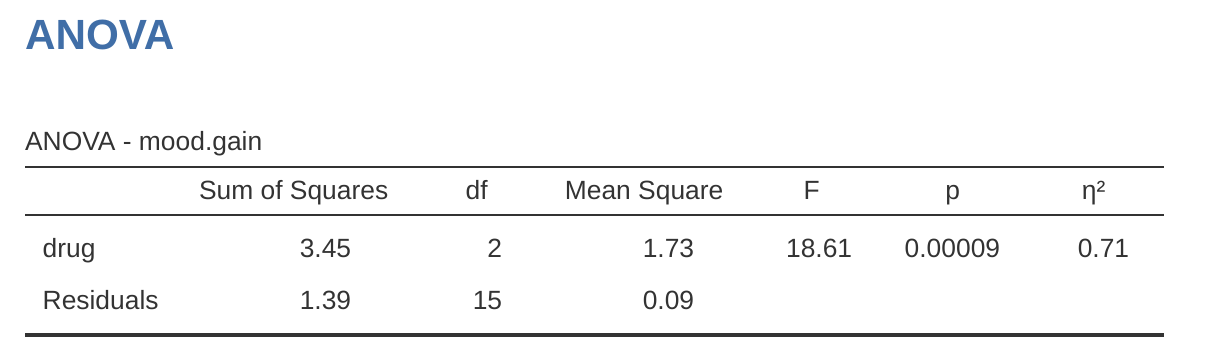
jamovi 的結果表格顯示了平方和值、自由度以及我們現在並不真正感興趣的其他一些數量。然而,請注意,jamovi 不使用「組間」和「組內」這兩個名稱。 相反,它嘗試分配更有意義的名稱。 在我們的特定示例中,組間方差對應於藥物對結果變項的影響,組內方差對應於“剩餘”的可變性,因此它將其稱為殘差。 如果我們將這些數字與 [A worked example] 中我手工計算的數字進行比較,可以看到它們或多或少是相同的,除了四捨五入誤差。組間平方和為 \(SS_b = 3.45\),組內平方和為 \(SS_w = 1.39\),各自的自由度為 \(2\) 和 \(15\)。我們還得到了 F 值和 p 值,同樣,這些數字與我們在手工計算時的數字差不多相同,只是四捨五入誤差。
12.4 效果量
有幾種不同的方法可以衡量 ANOVA 中的效應大小,但最常用的衡量指標是 \(\eta^2\)(eta 平方)和偏 \(\eta^2\)。對於單因素變異數分析,它們彼此相同,所以目前我只解釋 \(\eta^2\)。\(\eta^2\) 的定義實際上非常簡單:
\[\eta^2=\frac{SS_b}{SS_{tot}}\]
就是這樣。所以當我查看 Figure 12.3 中的 ANOVA 表時,我看到 \(SS_b = 3.45\) 和 \(SS_tot = 3.45 + 1.39 = 4.84\)。因此,我們得到一個 \(\eta^2\) 值:
\[\eta^2=\frac{3.45}{4.84}=0.71\]
\(\eta^2\) 的解釋同樣直接。它表示可以根據預測變項(藥物)解釋的結果變項(mood.gain)可變性的比例。\(\eta^2=0\) 表示兩者之間完全沒有關係,而 \(\eta^2=1\) 表示關係是完美的。更好的是,\(\eta^2\) 值與 Section 10.6.1 中討論的 \(R^2\) 關係非常密切,並具有等效的解釋。儘管許多統計教科書建議在 ANOVA 中使用 \(\eta^2\) 作為默認的效應大小衡量指標,但 Daniel Lakens 的一篇有趣的博客文章表明,eta 平方在實際數據分析中可能不是最好的效應大小衡量指標,因為它可能是一個有偏估計量。有用的是,jamovi 中還有一個選項可以指定 ω 平方(\(\omega^2\)),它與 η 平方相比偏差較小。
12.5 多重比較與事後檢定
每當您對多於兩個組進行 ANOVA,並得到顯著效應時,您可能首先想問的是哪些組之間實際上存在差異。在我們的藥物示例中,我們的零假設是所有三種藥物(安慰劑、Anxifree 和 Joyzepam)對情緒的影響完全相同。但是如果你仔細想一想,實際上零假設一次聲稱了三個不同的事情。具體來說,它聲稱:
- 您的競爭對手的藥物(Anxifree)並不比安慰劑更好(即,\(\mu_A = \mu_P\) )
- 您的藥物(Joyzepam)並不比安慰劑更好(即,\(\mu_J = \mu_P\) )
- Anxifree 和 Joyzepam 同樣有效(即,\(\mu_J = \mu_A\))
如果上述三個聲稱中的任何一個是偽的,那麼零假設也是偽的。因此,現在我們已經拒絕了我們的零假設,我們認為至少有一件事是不正確的。但哪些呢?所有三個命題都很有趣。既然您肯定想知道您的新藥 Joyzepam 是否比安慰劑更好,那麼了解它與現有商業替代品(即 Anxifree)的比較如何就變得很重要了。甚至有用的是檢查 Anxifree 與安慰劑的表現。即使 Anxifree 已經被其他研究人員廣泛地與安慰劑進行了對照測試,但檢查您的研究是否產生了與早期工作相似的結果仍然非常有用。
當我們根據這三個不同的命題來描述零假設時,我們需要區分的八種可能的“世界狀態”變得清晰了( Table 12.9 )。
| possibility: | is \( \mu_P = \mu_A \)? | is \( \mu_P = \mu_J \)? | is \( \mu_A = \mu_J \)? | which hypothesis? |
|---|---|---|---|---|
| 1 | \( \checkmark \) | \( \checkmark \) | \( \checkmark \) | null |
| 2 | \( \checkmark \) | \( \checkmark \) | alternative | |
| 3 | \( \checkmark \) | \( \checkmark \) | alternative | |
| 4 | \( \checkmark \) | alternative | ||
| 5 | \( \checkmark \) | \( \checkmark \) | \( \checkmark \) | alternative |
| 6 | \( \checkmark \) | alternative | ||
| 7 | \( \checkmark \) | alternative | ||
| 8 | alternative |
通過拒絕零假設,我們已經決定我們不相信 #1 是真實的世界狀態。下一個問題是,我們認為其他七個可能性中的哪一個*是對的?面對這種情況,通常最好先看看數據。例如,如果我們查看 Figure 12.1 中的繪圖,我們很容易得出 Joyzepam 優於安慰劑和 Anxifree,但 Anxifree 和安慰劑之間沒有實際差別的結論。然而,如果我們想對此得到更清晰的答案,則可能需要進行一些測試。
12.5.1 成對t檢定
我們如何解決問題?考慮到我們需要比較三對不同的平均值(安慰劑對 Anxifree,安慰劑對 Joyzepam,和 Anxifree 對 Joyzepam),我們可以執行三個單獨的 t 檢驗,看看會發生什麼。在 jamovi 中這很容易做到。轉到 ANOVA 的 ‘Post Hoc Tests’(事後檢驗)選項,將 ‘drug’(藥物)變項移到右側的活動框中,然後單擊 ‘No correction’(無校正)複選框。這將產生一個整齊的表格,顯示藥物變項的三個水平之間的所有成對 t 檢驗比較,如 Figure 12.4 中所示。
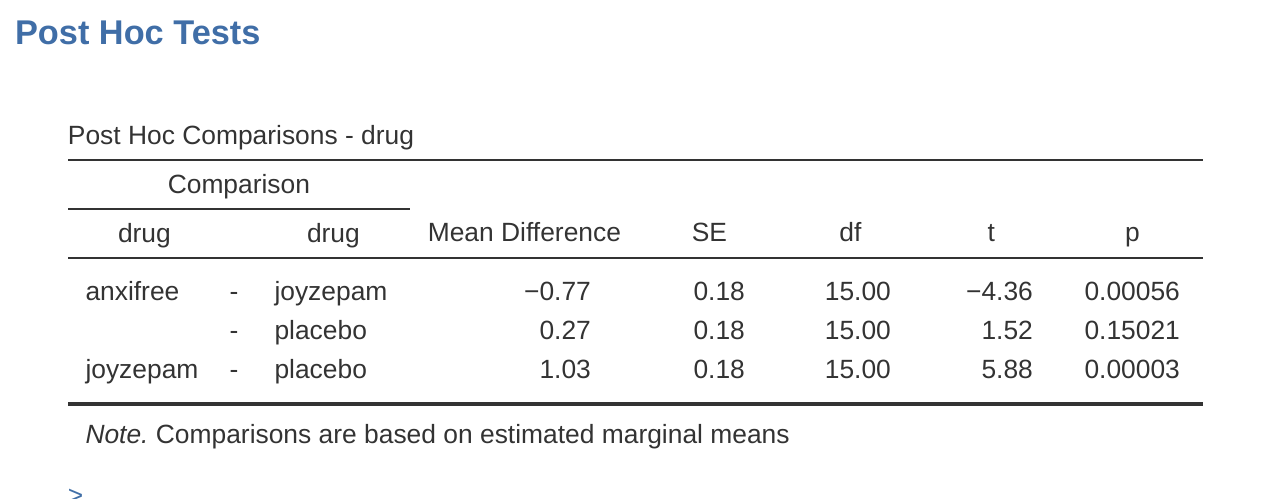
12.5.2 多重檢定的校正
在上一節中,我暗示了執行大量 t 檢驗存在問題。我們擔心的是,在執行這些分析時,我們正在進行一個「捕魚之旅」。我們在沒有太多理論指導的情況下執行了大量測試,希望其中一些測試顯示出顯著性。這種對團體差異的無理論基礎的搜索被稱為事後分析(“post hoc” 是拉丁語,意為 “after this”)。[^13-comparing-several-means-one-way-anova-10]
[^13-comparing-several-means-one-way-anova-10]:如果您確實有一些理論基礎,希望研究某些比較而不是其他比較,那就是另一回事了。在這種情況下,您實際上並不是在執行「事後分析」,而是在進行「預先計劃的比較」。我確實在本書後面談到了這種情況- Section 13.9 ,但現在我想保持簡單。
進行事後分析是可以的,但需要非常小心。例如,在上一節中進行的分析應該避免,因為每個單獨的 t 檢驗都設計為 5% 的第一型錯誤率(即 \(\alpha = .05\)),而我執行了其中的三個檢驗。想象一下,如果我的 ANOVA 涉及 10 個不同的組,我決定執行 45 個「事後」t 檢驗,試圖找出哪些組之間存在顯著差異,那麼僅憑機會就會出現 2 到 3 個顯著結果。正如我們在 Chapter 9 中看到的那樣,虛無假設檢驗背後的核心組織原則是控制我們的第一型錯誤率,但是現在,由於我同時執行了大量 t 檢驗以確定 ANOVA 結果的來源,整個試驗家族的實際第一型錯誤率已經完全失控。
解決這個問題的常用方法是對 p 值進行調整,目的是控制整個試驗家族的總誤差率(參見 Shaffer (1995))。這種調整通常(但不總是)應用於事後分析,通常被稱為多重比較校正,儘管有時也被稱為「同時推斷」。無論如何,進行這種調整的方法有很多。我將在本節和下一章節 Section 13.8 中討論其中的一些方法,但您應該意識到還有很多其他方法(例如,參見 Hsu (1996) )。
12.5.3 Bonferroni校正
這些調整中最簡單的一種被稱為邦弗隆尼校正(Dunn, 1961),它確實非常簡單。假設我的事後分析包括 m 個單獨的檢驗,我希望確保出現任何第一型錯誤的總概率最多為 \(\alpha\)。[^13-comparing-several-means-one-way-anova-11] 如果是這樣,那麼邦弗隆尼校正只是說「將所有原始 p 值乘以 m」。如果讓 \(p\) 表示原始 p 值,讓 \(p_j^{'}\) 表示經過校正的值,那麼邦弗隆尼校正告訴我們:
[^13-comparing-several-means-one-way-anova-11]:順便值得一提的是,並非所有調整方法都試圖這樣做。我在這裡描述的是一種用於控制「家族式第一型錯誤率」的方法。然而,還有其他事後檢驗試圖控制「偽發現率」,這是一個有點不同的概念。
\[p_j^{'}=m \times p\]
因此,如果您使用邦弗隆尼校正,則在 \(p_j^{'} < \alpha\) 的情況下拒絕零假設。這種校正背後的邏輯非常簡單。我們正在進行 m 個不同的檢驗,因此,如果我們安排使每個檢驗的第一型錯誤率至多為 \(\frac{\alpha}{m}\),那麼這些檢驗的總第一型錯誤率不能大於 \(\alpha\)。這很簡單,簡單到在原始論文中,作者寫道:
在這裡給出的方法如此簡單,而且如此通用,我確信它肯定已經被使用過了。然而,我沒有找到它,所以只能得出一個結論:也許正是它的極簡單讓統計學家意識不到它在某些情況下是一個非常好的方法(Dunn (1961),第52-53頁)。
要在 jamovi 中使用邦弗隆尼校正,只需單擊「校正」選項中的「邦弗隆尼」復選框,您將在 ANOVA 結果表中看到另一列,顯示邦弗隆尼校正的調整後 p 值( Table 12.8 )。如果我們將這三個 p 值與未校正的成對 t 檢驗的 p 值進行比較,很明顯 jamovi 所做的唯一事情就是將它們乘以 \(3\)。
12.5.4 Holm校正
雖然邦弗隆尼校正是最簡單的調整方法,但它通常不是最好的選擇。經常使用的另一種方法是霍爾姆校正(Holm correction)(Holm, 1979)。霍爾姆校正背後的思路是假設您正在按順序進行測試,從最小(原始)的 p 值開始,然後移動到最大的 p 值。對於第 j 大的 p 值,調整是以下兩者之一
\[p_j^{'}=j \times p_j\]
(即最大的 p 值保持不變,第二大的 p 值翻倍,第三大的 p 值翻三倍,依此類推),或者
\[p_j^{'}=p_{j+1}^{'}\]
其中較大者。這可能聽起來有點困惑,所以讓我們慢慢解釋。霍爾姆校正的工作原理如下。首先,您按順序對所有 p 值進行排序,從最小到最大。對於最小的 p 值,您只需將其乘以 \(m\),然後就完成了。然而,對於其他所有的 p 值,這是一個兩階段的過程。例如,當您移動到第二小的 p 值時,首先將其乘以 \(m - 1\)。如果這產生的數字大於您上次得到的調整後的 p 值,那麼保留它。但如果它比上一個小,那麼您將複製上一個 p 值。為了說明這是如何工作的,請考慮 Table 12.10 ,該表顯示了五個 p 值的霍爾姆校正計算。
| raw p | rank j | p \( \times \) j | Holm p |
|---|---|---|---|
| .001 | 5 | .005 | .005 |
| .005 | 4 | .020 | .020 |
| .019 | 3 | .057 | .057 |
| .022 | 2 | .044 | .057 |
| .103 | 1 | .103 | .103 |
希望這能讓事情變得清晰。
雖然計算起來稍微困難一些,但霍爾姆校正具有一些非常好的特性。它比邦弗隆尼更具威力(即具有更低的 Type II 錯誤率),但是,儘管可能令人反直覺,它具有相同的 Type I 錯誤率。因此,在實踐中,沒有理由使用更簡單的邦弗隆尼校正,因為它總是被稍微複雜一點的霍爾姆校正所超越。正因為如此,霍爾姆校正應該是您的首選多重比較校正。 Figure 12.4 還顯示了霍爾姆校正後的 p 值,如您所見,最大的 p 值(對應於 Anxifree 和安慰劑之間的比較)沒有改變。它的值為 .15,與我們最初在完全不做校正時得到的值完全相同。相比之下,最小的 p 值(Joyzepam 與安慰劑)已乘以三。
12.5.5 事後檢定的報告格式
最後,在執行事後分析以確定哪些組別之間的差異顯著之後,您可以這樣寫出結果:
事後檢驗(使用霍爾姆校正來調整 p 值)表明,與 Anxifree(p = .001)和安慰劑(\((p = 9.0 \times{10^{-5}}\))相比,Joyzepam 產生了顯著更大的心情變化。我們沒有發現 Anxifree 表現優於安慰劑的證據(\(p = .15\))。
或者,如果您不喜歡報告精確的 p 值,那麼分別將這些數字更改為 \(p < .01\)、\(p < .001\) 和 \(p > .05\)。無論哪種方式,關鍵是要表明您使用了霍爾姆的校正來調整 p 值。當然,我假設在撰寫的其他部分,您已經包括了相關的描述性統計資料(即組平均值和標準差),因為這些 p 值本身並不是很有信息量。
12.6 單因子變異數分析的適用條件
像任何統計檢驗一樣,變異數分析依賴於關於數據(特別是殘差)的一些假設。您需要了解三個關鍵假設:正態性、方差同質性和獨立性。
[額外的技術細節 [^13-comparing-several-means-one-way-anova-12]]
[^13-comparing-several-means-one-way-anova-12]:如果您記得回到[一個實例],我希望您至少瀏覽了一遍,即使您沒有讀完整篇文章,我以這種方式描述了支撐ANOVA的統計模型:\[H_0:Y_{ik}=\mu + \epsilon_{ik}\] \[H_1:Y_{ik}=\mu_k + \epsilon_{ik}\]在這些等式中,\(\mu\)指的是對所有組別都相同的單個總群體均值,µk是第k個組的群體均值。到目前為止,我們主要關心的是我們的數據是最好用單個總均值(零假設)來描述,還是用不同的特定組均值(替代假設)來描述。當然,這是有道理的,因為這實際上是重要的研究問題!然而,我們所有的檢驗過程都是在一個關於殘差 \(\epsilon_{ik}\) 的具體假設下進行的,即:\[\epsilon_{ik} \sim Normal(0,\sigma^2)\]如果沒有這部分,所有的數學都不能正常工作。或者,確切地說,您仍然可以進行所有計算,最終得到一個F統計量,但是您無法保證這個F統計量實際上衡量了您認為它衡量的內容,因此您可能基於F檢驗得出的任何結論都可能是錯誤的。
那麼,我們如何檢查對殘差的假設是否準確呢?嗯,正如我上面所指出的,這個陳述中隱含了三個不同的主張,我們將分別考慮它們。
- 方差同質性。注意到我們只有一個群體標準差的值(即,\(\sigma\)),而不是讓每個組都有它自己的值(即,\(\sigma_k\))。這被稱為方差同質性(有時稱為等方差性)假設。ANOVA假定所有組的群體標準差相同。我們將在[檢查方差同質性假設]部分詳細論述這一點。
- 正態性。假定殘差呈正態分布。正如我們在 Section 11.9 中看到的,我們可以通過查看QQ圖(或運行Shapiro-Wilk檢驗)來評估這一點。我將在[檢查正態性假設]部分中更多地討論這個問題。
- 獨立性。獨立性假設有點棘手。它基本上的意思是,了解一個殘差對於了解任何其他殘差都沒有幫助。所有的 \(\epsilon_{ik}\) 值都被假定是在不考慮或與其他任何值無關的情況下生成的。對於這一點,沒有顯而易見或簡單的檢驗方法,但有些情況是明顯違反這一假設的。例如,如果您有一個重複測量設計,每個參與者在研究中出現在多個條件下,那麼獨立性就不成立了。在這種情況下,某些觀察之間存在特殊關係,即對應於同一個人的觀察!當這種情況發生時,您需要使用類似[重複測量單因子ANOVA]的方法。
12.6.1 同質性檢核
要進行方差的初步檢驗,就像乘坐划艇出海,看看海面條件是否足夠平靜,讓一艘大型遊輪離港!
– 喬治·博克斯 (Box, 1953)
俗話說,殺貓有很多方法,檢驗方差同質性假設也有很多方法(不過出於某種原因,沒有人把它變成一句俗話)。在文獻中,我見過的最常用的檢驗方法是Levene檢驗(Levene, 1960),以及與之密切相關的Brown-Forsythe檢驗(Brown & Forsythe, 1974)。
無論您是進行標準Levene檢驗還是Brown-Forsythe檢驗,檢驗統計量(有時表示為\(F\),但也有時表示為\(W\)),都是按照計算常規ANOVA中的F-統計量的方式,只是使用\(Z_{ik}\)而不是\(Y_{ik}\)。有了這個思路,我們可以繼續看看如何在jamovi中運行檢驗。
[額外的技術細節[^13-comparing-several-means-one-way-anova-13]]
[^13-comparing-several-means-one-way-anova-13]:Levene檢驗非常簡單。假設我們有結果變項\(Y_{ik}\)。我們所要做的就是定義一個新變項,我將其稱為\(Z_{ik}\),表示與組均值的絕對偏差:\[Z_{ik}=Y_{ik}-\bar{Y}_{k}\]好吧,這對我們有什麼好處呢?那麼,讓我們花一點時間來思考一下\(Z_{ik}\)到底是什麼以及我們要檢驗什麼。\(Z_{ik}\)的值是度量第\(i\)次觀測在第\(k\)個組中與其組平均值的偏差程度。我們的零假設是所有組的方差都相同,即所有組平均值的總偏差相同!因此,Levene檢驗中的零假設是所有組的\(Z\)的母體平均值相同。嗯。那麼我們現在需要的是一個統計檢驗來檢驗所有組均值相同的零假設。我們在哪裡見過這個檢驗?哦對了,這就是ANOVA,所以Levene檢驗所做的就是對新變項\(Z_{ik}\)進行ANOVA。Brown-Forsythe檢驗呢?它有做什麼特別不同的事情嗎?不,與Levene檢驗唯一的不同是它以稍微不同的方式構建轉換變項Z,使用組中位數的偏差而不是組平均值的偏差。也就是說,對於Brown-Forsythe檢驗:\[Z_{ik}=Y_{ik}-median_k(Y)\]其中,\(median_k(Y)\)是第k組的中位數。
12.6.2 jamovi的Levene檢定
好的,那麼我們該如何進行Levene檢驗呢?其實很簡單 - 在ANOVA的”假設檢查”選項下,只需點擊”變異數同質性檢驗”複選框。如果我們查看 Figure 12.5 中的輸出,我們可以看到檢驗結果並無顯著差異(\(F_{2,15} = 1.45, p = .266\)),所以變異數同質性假設看起來沒有問題。然而,外表可能會讓人受騙!如果您的樣本量相當大,那麼即使變異數同質性假設沒有被違反到影響ANOVA的穩健性,Levene檢驗也可能顯示出顯著效應(即p < .05)。這正是George Box在上面引述中所指出的觀點。同樣地,如果您的樣本量相當小,那麼變異數同質性假設可能不被滿足,而Levene檢驗可能不顯著(即p > .05)。這意味著,在對假設是否被滿足進行任何統計檢驗的同時,您應該總是繪製每個分組/類別的均值周圍的標準差……只是為了看看它們是否看起來相當相似(即變異數同質性)或不相似。
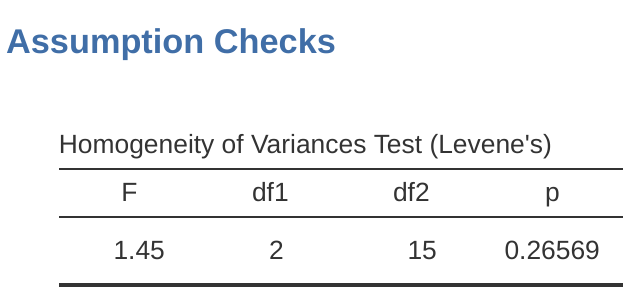
12.6.3 校正異質性的分析結果
在我們的示例中,變異數同質性假設被證明是相當可靠的:Levene檢驗結果並無顯著差異(儘管我們還應該查看標準差的圖形),因此我們可能不需要擔心。然而,在現實生活中,我們並非總是如此幸運。當變異數同質性假設被違反時,我們該如何拯救我們的ANOVA呢?如果您回想一下我們對t檢驗的討論,我們之前遇到過這個問題。Student t檢驗假設等方差,所以解決方法是使用不需要等方差假設的Welch t檢驗。實際上, Welch (1951) 還展示了我們如何解決ANOVA的這個問題(Welch單因素檢驗)。它在jamovi中使用One-Way ANOVA分析實現。這是一種專為單因素ANOVA設計的分析方法,要在我們的示例中執行Welch單因素ANOVA,我們將按照之前的方式重新運行分析,但這次使用jamovi的ANOVA - One Way ANOVA分析命令,並選擇Welch檢驗的選項(參見 Figure 12.6 )。為了理解這裡發生了什麼,讓我們將這些數字與我們在[最初在jamovi中運行ANOVA]時得到的數字進行比較。為了省去您回顧的麻煩,上次我們得到的是:\(F(2, 15) = 18.611, p = .00009\),這也顯示為 Figure 12.6 中One-Way ANOVA的Fisher檢驗。
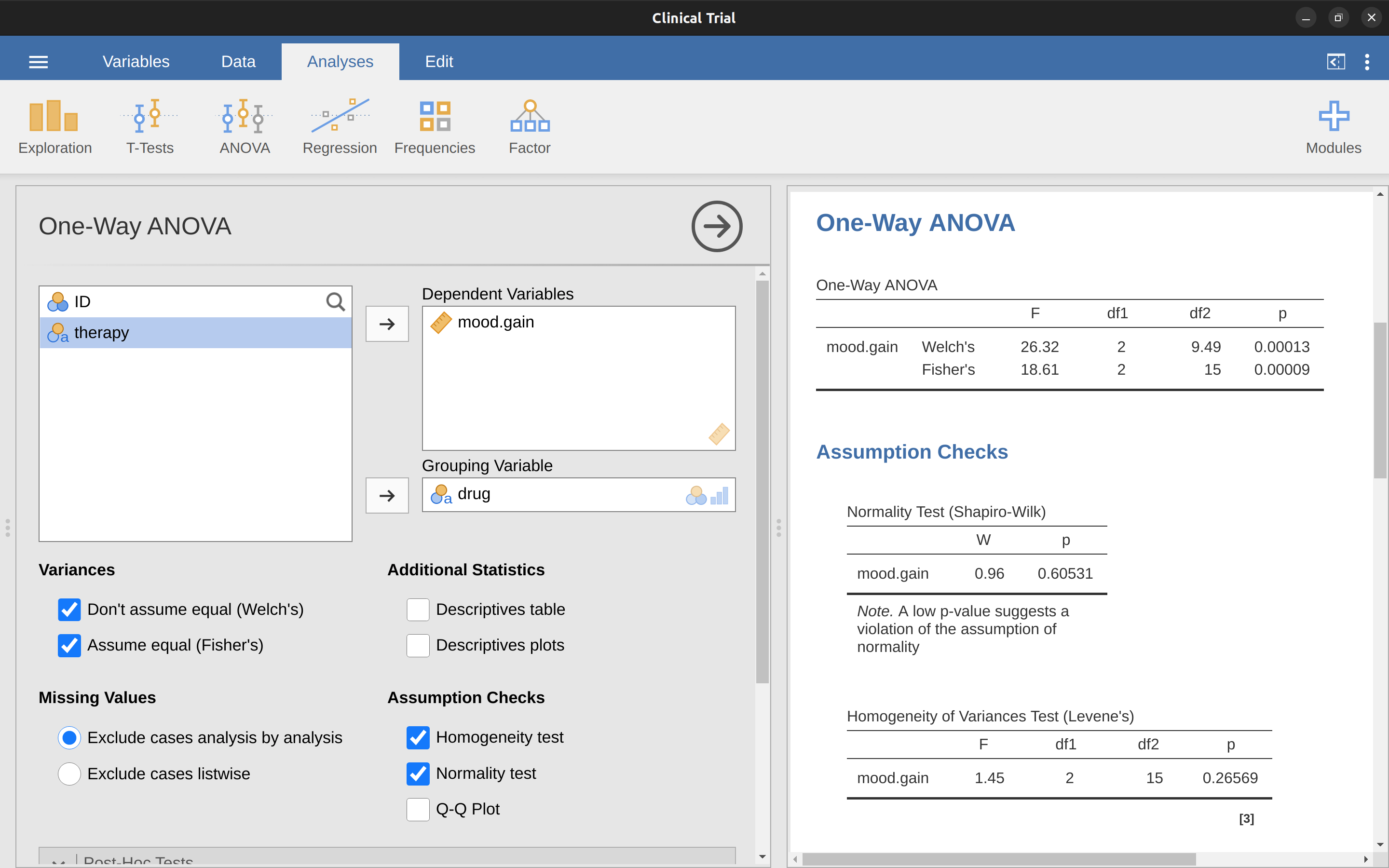
好的,最初我們的ANOVA結果是\(F(2, 15) = 18.6\),而Welch單因素檢驗給出的是\(F(2, 9.49) = 26.32\)。換句話說,Welch檢驗將組內自由度從15降低到了9.49,而F值從18.6上升到了26.32。
12.6.4 常態性檢核
檢驗正態性假設相對簡單。我們在 Section 11.9 中介紹了大部分你需要了解的內容。我們真正需要做的只是繪製一個QQ圖,並在可行的情況下,運行Shapiro-Wilk檢驗。QQ圖顯示在 Figure 12.7 ,對我來說看起來相當正常。如果Shapiro-Wilk檢驗不顯著(即\(p > .05\)),那麼這表明正態性假設沒有被違反。然而,與Levene檢驗一樣,如果樣本量很大,那麼顯著的Shapiro-Wilk檢驗實際上可能是偽陽性,也就是說,正態性假設在實質上沒有對分析造成任何問題。同樣地,非常小的樣本量可能會產生偽陰性。這就是為什麼視覺檢查QQ圖很重要。
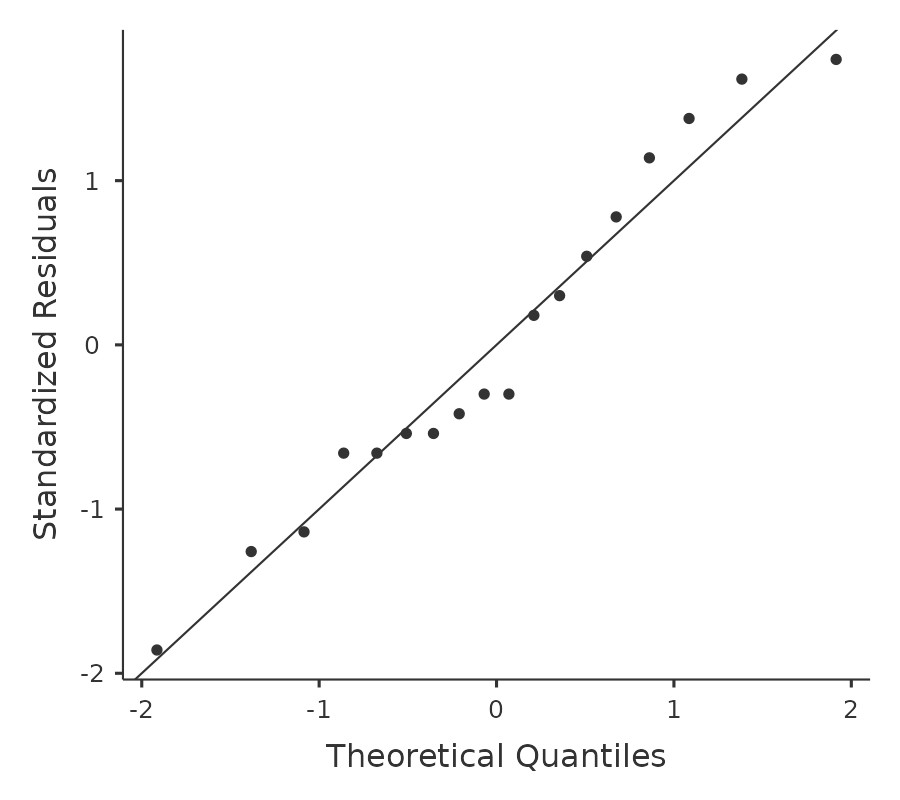
除了檢查QQ圖中是否有偏離正態性的情況外,我們的數據的Shapiro-Wilk檢驗確實顯示出非顯著效應,p = 0.6053(見 Figure 12.6 )。因此,這支持了QQ圖的評估;兩個檢查都沒有發現正態性被違反的跡象。
12.6.5 排除非常態性的分析結果
現在我們已經了解了如何檢查正態性,我們自然會問可以採取哪些措施來解決正態性的違反。在單因素ANOVA的背景下,最簡單的解決方案可能是轉向非參數檢驗(即不依賴於任何特定的分佈假設的檢驗)。在 Chapter 11 中,我們之前已經介紹過非參數檢驗。當你只有兩個組別時,Mann-Whitney或Wilcoxon檢驗可以提供你所需的非參數替代方法。當你有三個或更多組別時,你可以使用Kruskal-Wallis秩和檢驗(Kruskal & Wallis, 1952)。接下來我們將講解這個檢驗。
12.6.6 Kruskal-Wallis檢定的邏輯
Kruskal-Wallis檢驗在某些方面與ANOVA驚人地相似。在ANOVA中,我們從\(Y_{ik}\)開始,對於第k個組中的第i個人,這是結果變項的值。對於Kruskal-Wallis檢驗,我們要做的是對所有的\(Y_{ik}\)值進行排序,並對排名數據進行分析。10
12.6.7 更多分析細節
上一節的描述說明了Kruskal-Wallis檢驗背後的邏輯。從概念上講,這是考慮測試如何工作的正確方法。[^13-comparing-several-means-one-way-anova-15]
[^13-comparing-several-means-one-way-anova-15]:然而,從純粹的數學角度來看,這是不必要的複雜。我不會向您展示推導,但您可以使用一些代數技巧\(^b\)來顯示K的方程式可以是\[K=\frac{12}{N(N-1)}\sum_k N_k \bar{R}_k^2 -3(N+1)\] 最後一個方程式有時給出了K的值。這比我在上一節中描述的版本要容易得多,但問題是對實際人類完全沒有意義。將K視為基於排名的ANOVA類比可能是最好的方式。但請記住,計算出來的檢驗統計量與我們最初用於ANOVA的統計量有很大不同。
—
\(b\)就是一些數學運算術語。
但等等,還有更多!天啊,為什麼總是有更多呢?到目前為止,我講的故事實際上只在原始數據中沒有相同數值的情況下才成立。也就是說,如果沒有兩個觀測值具有完全相同的值。如果有相同的值,那麼我們必須引入一個校正因子來進行這些計算。在這一點上,我假設即使是最勤奮的讀者也已經不再關心(或者至少形成了繫結校正因子不需要他們立即關注的看法)。因此,我將非常快速地告訴您如何計算它,並省略為什麼以這種方式進行的繁瑣細節。假設我們為原始數據構建一個頻率表,讓fj表示具有第j個唯一值的觀測值的數量。這聽起來可能有點抽象,因此我們將從clinicaltrials.csv數據集中的mood.gain頻率表( Table 12.11 )給出一個具體的例子。
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.8 | 0.9 | 1.1 | 1.2 | 1.3 | 1.4 | 1.7 | 1.8 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 2 | 2 | 1 | 1 |
觀察此表,請注意頻率表中的第三個條目值為2。由於這對應於心情增益為0.3,因此此表告訴我們有兩個人的心情增加了0.3。[^13-comparing-several-means-one-way-anova-16]
[^13-comparing-several-means-one-way-anova-16]:更重要的是,在我上面介紹的數學表示法中,這告訴我們\(f_3 = 2\)。耶。那麼,現在我們知道了這一點,繫結校正因子(TCF)是:\[TCF=1-\frac{\sum_j f_j^3 - f_j}{N^3 - N}\]通過將K值除以這個數量,可以得到Kruskal-Wallis統計量的繫結校正值。這是jamovi計算的繫結校正版本。
因此,jamovi使用繫結校正因子來計算繫結校正的Kruskall-Wallis統計量。最後,我們實際上已經完成了Kruskal-Wallis檢驗的理論。我確信你們都對我治愈了你們在意識到你們不知道如何計算Kruskal-Wallis檢驗的繫結校正因子時自然產生的存在焦慮感到非常寬慰。對吧?
12.6.8 使用jamovi完成Kruskal-Wallis檢定
儘管我們在努力理解Kruskal Wallis檢驗實際上做了什麼方面經歷了恐懼,但事實證明,進行該檢驗相當無痛,因為jamovi在ANOVA分析集中有一個名為「非參數」-「單因子ANOVA(Kruskall-Wallis)」的分析。大多數時候,你將擁有像clinicaltrial.csv這樣的數據集,其中包含你的結果變項mood.gain和一個分組變項drug。如果是這樣,你可以直接在jamovi中運行分析。這給我們提供了一個Kruskal-Wallis \(\chi^2 =12.076, df = 2, p = 0.00239\),如 Figure 12.8 所示。
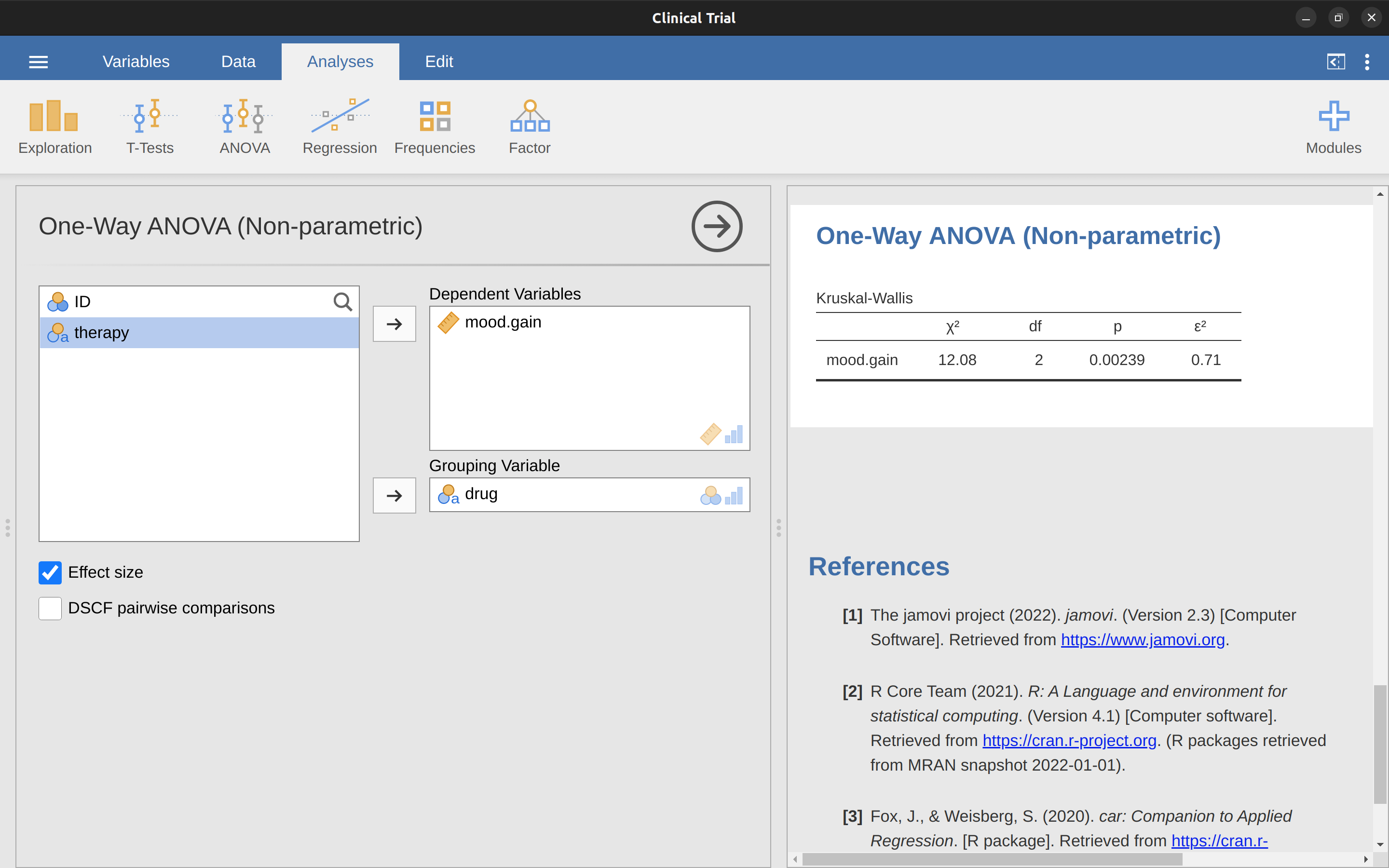
12.7 單因子重覆量數變異數分析
單因子重覆量數變數分析檢驗是一種統計方法,用於檢驗三個或更多組之間的顯著差異,其中每個組都使用相同的參與者(或者每個參與者與其他實驗組的參與者密切匹配)。因此,每個實驗組中應該始終具有相等數量的分數(數據點)。這種類型的設計和分析也可以稱為「相關ANOVA」或「內部主題ANOVA」。
重覆量數變數分析的邏輯與獨立ANOVA(有時稱為「間題」ANOVA)非常相似。您可能還記得,我們之前顯示在一個間題ANOVA總變異性可以分為組間變異性(\(SS_b\))和組內變異性(\(SS_w\)),在將每個變異性除以相應的自由度後得到MSb和MSw(見表13.1),F比值計算為:
\[F=\frac{MS_b}{MS_w}\]
在重覆量數變數分析中,F比值的計算方式類似,但是在獨立ANOVA中,組內變異性(\(SS_w\))被用作\(MS_w\)的分母,而在重覆量數變數分析中,\(SS_w\)被劃分為兩部分。由於我們在每個組中都使用相同的受試者,因此可以從組內變異性中移除受試者間個別差異(稱為SSsubjects)的變異性。我們不會深入討論這是如何實現的,但本質上,每個受試者都成為名為受試者的因子的一個水平。然後以與任何間題因子相同的方式計算此內部受試者因子中的變異性。然後我們可以將SSsubjects從\(SS_w\)中減去,以提供一個較小的SSerror項:
\[\text{獨立ANOVA: } SS_{error} = SS_w\] \[\text{重覆量數變數分析: } SS_{error} = SS_w - SS_{subjects}\] 這個\(SS_{error}\)項的變化通常會導致統計檢驗更加強大,但這確實取決於\(SS_{error}\)的減少是否超過了誤差項自由度的減少(因為自由度從\((n - k)\)11變為\((n - 1)(k - 1)\)(請記住,獨立ANOVA設計中的受試者更多)。
12.7.1 jamovi的重覆量數變異數分析
首先,我們需要一些數據。 Geschwind (1972) 表示,患者在中風後語言缺陷的確切性質可以用來診斷已受損的大腦特定區域。一位研究人員關心的是確定六位患有Broca失語症(中風後常見的語言缺陷)的患者所經歷的具體交流困難( Table 12.12 )。
| Participant | Speech | Conceptual | Syntax |
|---|---|---|---|
| 1 | 8 | 7 | 6 |
| 2 | 7 | 8 | 6 |
| 3 | 9 | 5 | 3 |
| 4 | 5 | 4 | 5 |
| 5 | 6 | 6 | 2 |
| 6 | 8 | 7 | 4 |
患者需要完成三個單詞識別任務。在第一個(言語生成)任務中,患者需要重複研究者大聲朗讀的單詞。在第二個(概念性)任務中,旨在測試單詞理解能力,患者需要將一系列圖片與其正確名稱匹配。在第三個(語法)任務中,旨在測試正確單詞順序的知識,要求患者對語法不正確的句子進行重新排序。每位患者都完成了所有三個任務。患者嘗試任務的順序在參與者之間進行了平衡。每個任務包括一系列10次嘗試。每位患者成功完成的嘗試次數如 Table 12.11 所示。將這些數據輸入jamovi以進行分析(或者使用捷徑加載broca.csv文件)。
要在jamovi中執行一個單因素相關ANOVA,打開一個單因素重覆量數變數分析對話框,如 Figure 12.9 中所示,通過ANOVA - Repeated Measures ANOVA進行。
然後:
- 輸入一個重複測量因子名稱。這應該是您選擇的標籤,用於描述所有參與者重複的條件。例如,要描述所有參與者完成的語音、概念和語法任務,一個合適的標籤是“任務”。請注意,這個新的因子名稱代表了分析中的自變項。
- 在重複測量因子文本框中添加第三個級別,因為有三個級別代表三個任務:語音、概念和語法。相應地更改級別的標籤。
- 然後將每個級別變項移動到重複測量單元文本框中。
- 最後,在“假設檢查”選項下,選中“球形性檢查”文本框。
jamovi輸出一個單因素重覆量數變數分析,如 Figure 12.10 至 Figure 12.13 所示。我們應該首先查看的是Mauchly球形性檢驗,該檢驗測試各條件之間的差異方差是否相等(意味著研究條件之間的差異得分的分佈大致相同)。在 Figure 12.10 中,Mauchly檢驗的顯著性水平為\(p = .720\)。如果Mauchly檢驗的結果不顯著(即p > .05,正如此分析中的情況),那麼我們有理由得出差異的方差並無顯著差異(即它們大致相等,可以假定球形性。)。

如果另一方面,Mauchly檢驗顯著(p < .05),那麼我們將得出差異方差之間存在顯著差異,並且未滿足球形性要求。在這種情況下,我們應該對單因素相關ANOVA分析中獲得的F值進行修正:
- 如果”球形性檢驗”表中的Greenhouse-Geisser值> .75,那麼您應該使用Huynh-Feldt修正
- 但如果Greenhouse-Geisser值< .75,那麼您應該使用Greenhouse-Geisser修正。
這兩個修正過的F值都可以在“假設檢查”選項下的球形性修正復選框中指定,修正過的F值將顯示在結果表中,如 Figure 12.11 所示。

在我們的分析中,我們發現Mauchly的球形性檢驗的顯著性為p = .720(即p > 0.05)。因此,這意味著我們可以假設已滿足球形性要求,因此無需對F值進行修正。因此,我們可以使用’無’球形性修正輸出值用於重複測量”任務”:\(F = 6.93\),\(df = 2\),\(p = .013\),我們可以得出結論,語言任務中成功完成的測試次數確實會根據任務是語音、理解還是語法為基礎而顯著不同(\(F(2, 10) = 6.93\),\(p = .013\))。
在jamovi中,與獨立ANOVA相同,也可以為重覆量數變數分析指定事後檢驗。結果顯示在 Figure 12.12 。這些表明語音和語法之間存在顯著差異,但其他級別之間沒有差異。
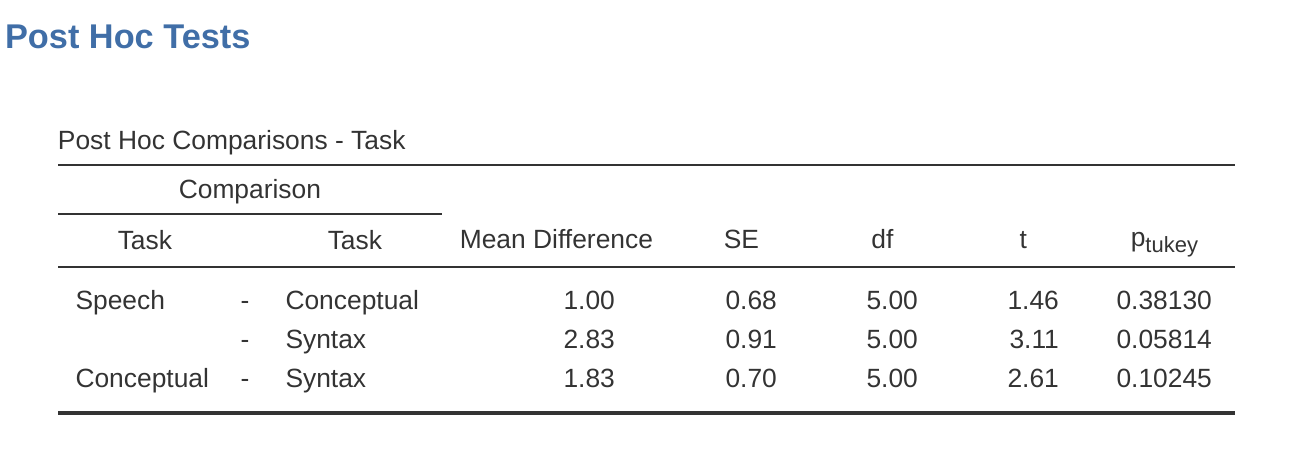
描述性統計(邊際均值)可以用於幫助解釋結果,在jamovi輸出中生成,如 Figure 12.13 。通過比較參與者成功完成試驗的平均次數,可以看出布洛卡失語症患者在語音產生(平均= 7.17)和語言理解(平均= 6.17)任務上表現相對較好。然而,他們在語法任務上的表現明顯較差(平均= 4.33),事後檢驗中語音和語法任務表現之間存在顯著差異。
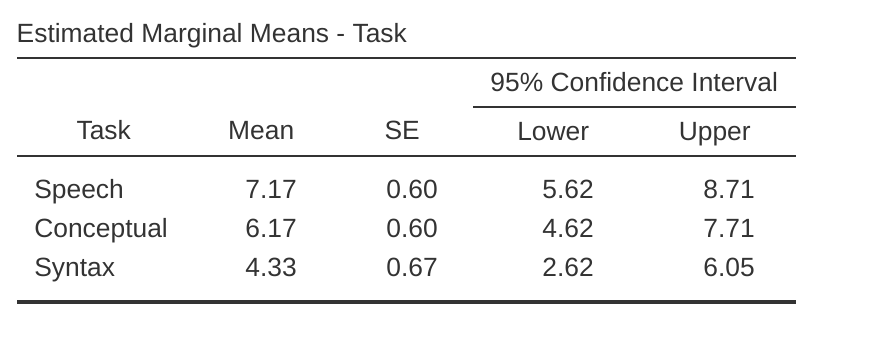
12.8 Friedman無母數重覆量數變異數分析
Friedman檢驗是一元重覆量數變數分析的非參數版本,可以在測試三個或更多組之間的差異時使用,其中每個組中的參與者相同,或者每個參與者與其他條件中的參與者密切匹配。如果因變項是序數,或者未滿足正態性假設,則可以使用Friedman檢驗。
與Kruskall-Wallis檢驗一樣,基本數學知識很複雜,這裡不會介紹。對於本書的目的,僅需注意jamovi計算了Friedman檢驗的綁定修正版本,在 Figure 12.14 中有一個我們已經查看過的布洛卡失語症數據的示例。
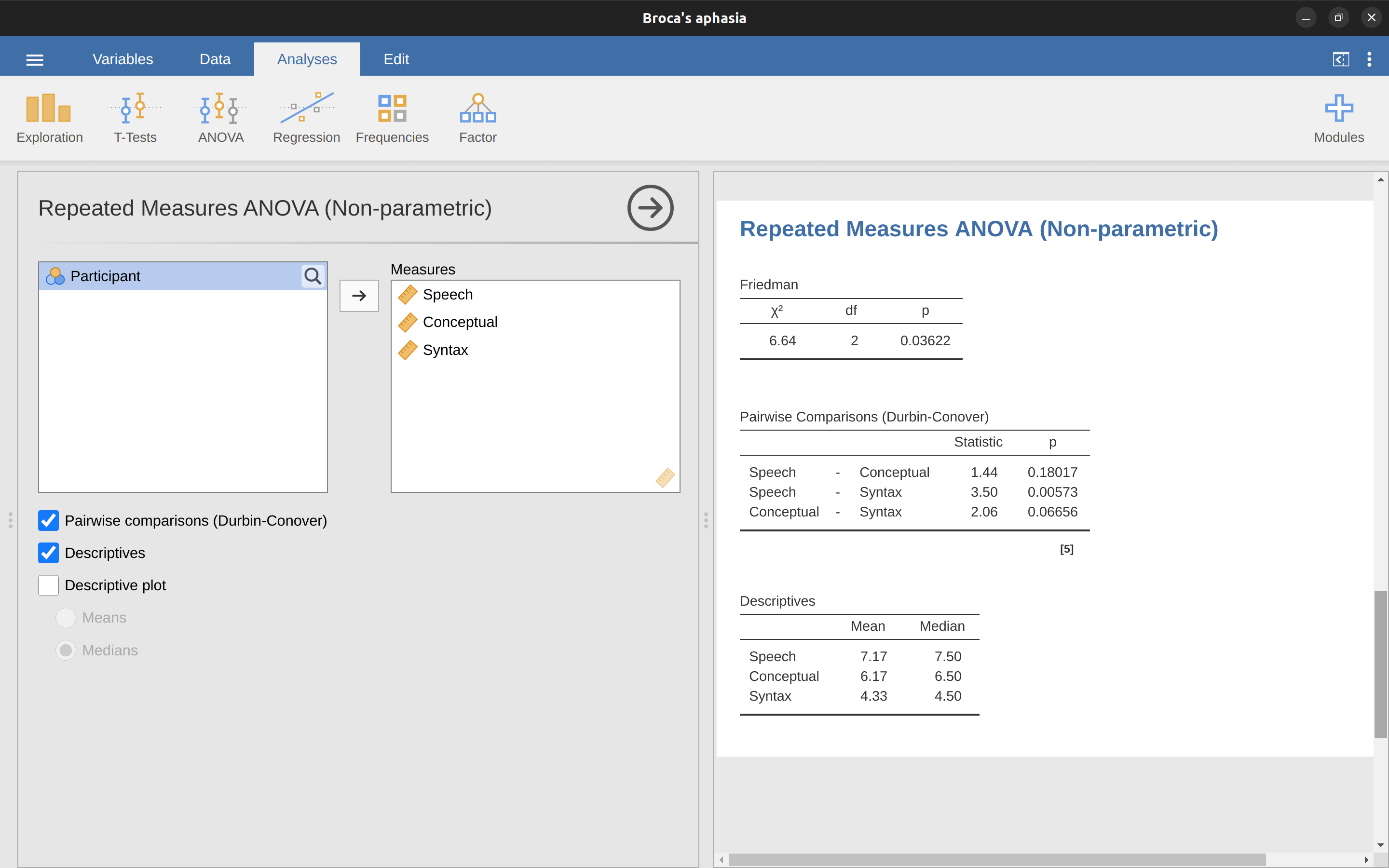
在jamovi中運行Friedman檢驗非常簡單。只需選擇分析 - ANOVA - 重覆量數變數分析(非參數),如 Figure 12.14 所示。然後將要比較的重複測量變項的名稱(語言、概念、語法)突顯並轉移到“測量:”文本框中。要為三個重複測量變項生成描述性統計(平均值和中位數),請單擊描述性按鈕。
jamovi結果顯示描述性統計、卡方值、自由度和p值( Figure 12.14 )。由於p值小於通常用於確定顯著性的水平(p < .05),我們可以得出結論,布洛卡失語症患者在語言生產(中位數= 7.5)和語言理解(中位數= 6.5)任務上表現相當好。然而,他們在語法任務上的表現明顯較差(中位數= 4.5),在事後檢驗中語言和語法任務表現之間存在顯著差異。
12.9 變異數分析與t檢定的關聯
在結束之前,我想指出的最後一點是,許多人對此感到驚訝,但了解它是很有價值的。具有兩個組別的ANOVA與學生t檢驗相同。不,真的。它們不僅相似,而且在每個有意義的方面實際上都是等效的。我不會試圖證明這總是成立,但我將給你展示一個具體的演示。假設,我們不對mood.gain ~ drug模型進行ANOVA,而是使用療法作為預測指標。如果我們運行此ANOVA,我們將得到一個F統計量 \(F(1,16) = 1.71\),和一個 p值 = \(0.21\)。由於我們只有兩組,實際上我不需要求助於ANOVA,我可以選擇運行一個學生t檢驗。那麼,讓我們看看這樣做會發生什麼:我得到一個t統計量 \(t(16) = -1.3068\) 和一個 \(p值 = 0.21\)。好奇的是,p值是相同的。再一次,我們得到一個值 \(p = .21\)。但是,檢驗統計量呢?運行t檢驗而不是ANOVA,我們得到了一個略有不同的答案,即 \(t(16) = -1.3068\)。然而,這裡有一個相當直接的關係。如果將t統計量平方,我們就會得到之前的F統計量:\(-1.3068^{2} = 1.7077\)
12.10 本章小結
這一章份量不少,但是有一些細節我並未提到12。最明顯的是在此並未討論處理不只一個分組變項的資料,我們在下一章 Chapter 13 將學習其中一部分。本章的學習重點有:
- 理解變異數分析的運作原理 以及使用jamovi完成變異數分析
- 學習如何計算變異數分析的效果量
- 多重比較與事後檢定
- 單因子變異數分析的執行條件
- 同質性檢核 以及 校正異質性的分析結果
- 常態性檢核以及排除非常態性的分析結果
- 單因子重覆量數變異數分析 以及其無母數版本單因子重覆量數變異數分析
當所有組的觀察值數目相同時,實驗設計被稱為“平衡”。對於本章介紹的單因子 ANOVA,平衡並不是很重要。當您開始進行更複雜的 ANOVA 時,它變得更重要。↩︎
所以總平方和的公式與方差的公式幾乎相同 \[SS_{tot}=\sum_{k=1}^{G} \sum_{i=1}^{N_k} (Y_{ik} - \bar{Y})^2\]↩︎
總平方和的一個很好的特點是,我們可以將其分解為兩種不同類型的變異。首先,我們可以談論組內平方和,其中我們檢查每個個體與其所屬組的平均值之間有多大不同 \[SS_{w}= \sum_{k=1}^{G} \sum_{i=1}^{N_k} (Y_{ik} - \bar{Y}_k)^2\],其中 \(\bar{Y}_k\) 是一個組平均值。在我們的例子中,\(\bar{Y}_k\) 將是給予第 k 種藥物的那些人所經歷的平均情緒變化。所以,我們不是將個人與實驗中所有人的平均值進行比較,而是僅將他們與同一組中的人進行比較。因此,您可能會發現 \(SS_w\) 的值小於總平方和,因為它完全忽略了任何組之間的差異,即藥物對人們情緒的不同影響。↩︎
為了量化這種變化的程度,我們要做的是計算組間平方和 \[ \begin{aligned} SS_{b} &= \sum_{k=1}^{G} \sum_{i=1}^{N_k} ( \bar{Y}_{k} - \bar{Y} )^2 \\ &= \sum_{k=1}^{G} N_k ( \bar{Y}_{k} - \bar{Y} )^2 \end{aligned} \]↩︎
SS_w 在獨立 ANOVA 中也被稱為誤差變異,即 \(SS_{error}\)。↩︎
在根本上,ANOVA 是兩個不同統計模型之間的競爭,\(H_0\) 和 \(H_1\)。當我在本節開始時描述虛無假設和替代假設時,關於這些模型實際上是什麼,我有點不精確。我現在將補救這一點,儘管您可能不會因此而喜歡我。如果您回憶一下,我們的虛無假設是所有組均值彼此相同。如果是這樣,那麼考慮結果變項 \(Y_{ik}\) 的自然方法是將個體分數描述為單一母體均值 µ,再加上與該母體均值的偏差。這個偏差通常用 \(\epsilon_{ik}\) 表示,傳統上稱為該觀察值的誤差或殘差。但要小心。就像我們在單詞“顯著”中看到的那樣,單詞“誤差”在統計學中具有與它的日常英語定義不完全相同的技術含義。在日常語言中,“誤差”暗示著某種錯誤,但在統計學中則不是這樣(至少不一定是這樣)。考慮到這一點,“殘差”這個詞比“誤差”這個詞更好。在統計學中,這兩個詞都表示“剩餘可變性”,也就是模型無法解釋的“東西”。在任何情況下,當我們將虛無假設寫成統計模型時,它看起來像這樣 \[Y_{ik}=\mu+\epsilon_{ik}\],其中我們做出這樣的假設(稍後討論),殘差值 \(\epsilon_{ik}\) 是正態分布的,平均值為 \(0\),標準差 \(\sigma\) 對於所有組都是相同的。使用我們在 [概率簡介] 中介紹的符號,我們將這樣的假設寫成 \[\epsilon_{ik} \sim Normal(0,\sigma^2)\] 那麼替代假設 \(H_1\) 呢?虛無假設和替代假設之間的唯一區別是,我們允許每個組具有不同的母體均值。因此,如果我們讓 \(\mu_k\) 表示我們實驗中第 k 個組的母體均值,那麼與 \(H_1\) 相對應的統計模型是 \[Y_{ik}=\mu_k+\epsilon_{ik}\],其中,我們再次假設誤差項是正態分布的,平均值為 0,標準差為 \(\sigma\)。也就是說,替代假設還假定 \(\epsilon \sim Normal(0,\sigma^2)\) 好的,既然我們已經更詳細地描述了 \(H_0\) 和 \(H_1\) 的統計模型,那麼現在很容易說清楚平均平方值是如何衡量的,以及這對於解釋 \(F\) 意味著什麼。我不會用證明來煩惱你,但事實證明,組內平均平方 \(MS_w\) 可以看作是誤差變異數 \(\sigma^2\) 的估計器。組間平均平方 \(MS_b\) 也是估計器,但它估計的是誤差變異數加上一個取決於組均值之間真正差異的數量。如果我們將這個數量稱為 \(Q\),那麼我們可以看到 F 統計量基本上是 \(^a\) \[F=\frac{\hat{Q}+\hat{\sigma}^2}{\hat{\sigma}^2}\] 其中,如果虛無假設為真,那麼真實值 \(Q = 0\),如果替代假設為真,則 Q < 0(例如, Hays (1994) ,ch. 10)。因此,作為基本要求,\(F\) 值必須大於 1 才有可能拒絕虛無假設。需要注意的是,這並不意味著 F 值不可能小於 1。這意味著,如果虛無假設為真,那麼 F 比值的抽樣分布的均值為 1 [^b],因此,我們需要看到 F 值大於 1 才能安全地拒絕虛無假設。為了更精確地說明抽樣分布,請注意,如果虛無假設為真,那麼 MSb 和 MSw 都是殘差 \(\epsilon_{ik}\) 的變異數的估計量。如果這些殘差是正態分布的,那麼你可能會懷疑 \(\epsilon_{ik}\) 的變異數估計是卡方分布的,因為(如 Section 7.6 中所討論的),這就是卡方分布的含義:當你對一堆正態分布的事物進行平方並將它們相加時,就會得到這樣的分布。而 F 分布(再次,根據定義)就是在兩個 \(\chi^2\) 分布的事物之間取比值時得到的分布,我們就有了我們的抽樣分布。顯然,當我說這些時,我省略了很多東西,但在廣泛的意義上,這確實是我們的抽樣分布來源。
—
\(^a\) 如果你已經提前閱讀 Chapter 13 ,並查看了如何用 \(\alpha_k\) 值來定義因子水平 k 上的「處理效應」(參見平衡設計,允許交互作用的因子 ANOVA 2 节),則發現 \(Q\) 是處理效應平方加權平均值,\(Q = \frac{(\sum_{k=1}^{G}N_k \alpha_k^2)}{(G-1)}\)
\(^b\) 或者,如果我們想要非常精確,是 \(1+\frac{2}{df_2-2}\)。↩︎或者,確切地說,像 “1899年那樣狂歡,當時我們沒有朋友,也沒有比做一些計算更好的事情可做,因為直到 1920 年左右,ANOVA 都不存在。”↩︎
在 Excel clinicaltrial-anova.xls 中,SSb 的值與上文中顯示的值(取整誤差!)略有不同,為 \(3.45\)。↩︎
與上文中的數字相比,jamovi 的結果更為準確,這是由於四捨五入誤差。↩︎
那麼,讓R_{ik}表示給第k個組的第i個成員的排名。現在,讓我們計算\(\bar{R}_k\),即第k個組觀察值的平均排名: \[\bar{R}_k=\frac{1}{N_k}\sum_i R_{ik}\],讓我們也計算\(\bar{R}\),即總平均排名:\[\bar{R}=\frac{1}{N}\sum_i\sum_k R_{ik}\] 現在我們已經做了這些,我們可以計算與總平均排名\(\bar{R}\)的平方偏差。當我們對個別分數進行這種計算時,即如果我們計算\((R_{ik} - \bar{R})^2\),那麼我們得到的是一個“非參數”的度量,用於表示第ik個觀察值與總平均排名的偏差程度。當我們計算組均值與總均值的平方偏差時,即如果我們計算\((R_{ik} - \bar{R})^2\),那麼我們得到的是一個非參數度量,用於表示該組與總平均排名的偏差程度。考慮到這一點,我們將遵循與ANOVA相同的邏輯,並定義我們的排名平方和度量,就像我們之前所做的那樣。首先,我們有我們的“總排名平方和”\[RSS_{tot}=\sum_k\sum_i (R_{ik}-\bar{R})^2\],我們可以像這樣定義“組間排名平方和” \[\begin{aligned} RSS_{b}& =\sum{k}\sum_{i}(\bar{R}_{k}-\bar{R})^2 \\ &= \sum_{k} N_k (\bar{R}_{k}-\bar{R})^2 \end{aligned}\] 因此,如果虛無假設成立,且根本沒有真正的組差異,則您會期望組間排名和\(RSS_b\)非常小,遠小於總排名和\(RSS_{tot}\)。從質量上看,這與我們在構建ANOVA F-統計量時發現的非常相似,但出於技術原因,Kruskal-Wallis檢驗統計量通常表示為K,其構建方式略有不同,\[K=(N-1) \times \frac{RSS_b}{RSS_{tot}}\] 如果虛無假設成立,那麼K的抽樣分布近似為自由度為\(G-1\)的卡方分布(其中\(G\)為組的數量)。 K的值越大,數據與虛無假設的一致性就越小,因此這是一個單邊檢驗。當K足夠大時,我們拒絕\(H_0\)。↩︎
(n-k):(受試者數量-組別數量)↩︎
就像其他章節,本章內容有許多參考來源,其中原作者參考最多的專書是 Sahai & Ageel (2000) 。這本書對初學者來說偏難,不過如果學到這裡,想知道更多變異數分析的數學原理,這本書是不錯的參考資源。↩︎