| 變項 | 最小值 | 最大值 | 平均值 | 中位數 | 標準差 | 四分位數間距 |
|---|---|---|---|---|---|---|
| 老爸的沮喪程度 | 41.00 | 91.00 | 63.71 | 62.00 | 10.05 | 14.00 |
| 老爸睡眠小時數 | 4.84 | 9.00 | 6.97 | 7.03 | 1.02 | 1.45 |
| 小嬰兒睡眠小時數 | 3.25 | 12.07 | 8.05 | 7.95 | 2.07 | 3.21 |
10 相關與線性迴歸
本章的學習目標是相關與線性迴歸。這些是用來分析預測變項及應變項關係的標準統計學工具。1
10.1 相關
這一節要談如何描述資料變項之間的關係,因此會不斷提到變項之間的相關。首先,讓我們看一下列在 Table 10.1 的本章示範資料描述統計。
10.1.1 示範資料
讓我們從一個與每個新生兒父母都息息相關的主題談起:睡眠。這裡使用的資料集是虛構的,但是來自本人(原作者)的真實經驗:我想知道我那剛出生的兒子的睡眠習慣對我個人的情緒有多大影響。假想我可以非常精確地評估我的沮喪分數,評分從0分(一點都不沮喪)到100分(像一個非常非常沮喪的老頭子),還有我每天都有測量我的沮喪分數、我的睡眠習慣和我兒子的睡眠習慣持續是100天。身為一位數位時代的書呆子,我把資料保存在一個名為parenthood.csv的檔案。匯入jamovi,我們可以看到四個變項:dani.sleep,baby.sleep,dani.grump和day。請注意,當您首次打開這份檔案,jamovi可能無法正確猜測每個變項的資料類型,同學可以自行修正:dani.sleep,baby.sleep,dani.grump和day都可以被指定為連續變項,而ID是一個名義且為整數的變項。2
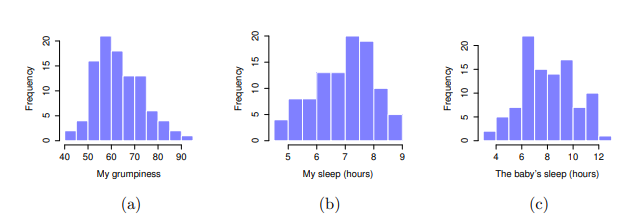
接著我會看一下一些基本的描述性統計數據,並且三個我有興趣的變項視覺化,也就是 Figure 10.1 展示的直方圖。需要注意的是,不要因為jamovi可以一次計算幾十種不同的統計數據,你就要報告所有數據。如果我要以此結果撰寫報告,我會挑出那些我自己以及我的讀者最感興趣的統計數據,然後將它們放入像 Table 10.1 這樣的簡潔的表格裡。3 需要注意的是,當我將數據放入表格時,我給了每個變項一個“高可讀性”的名稱。這是很好的做法。另外,請注意這一百天我都沒有睡飽,這不是好的習慣,不過其他帶過小孩的父母告訴我,這是很正常的事情。
10.1.2 相關的強度與方向
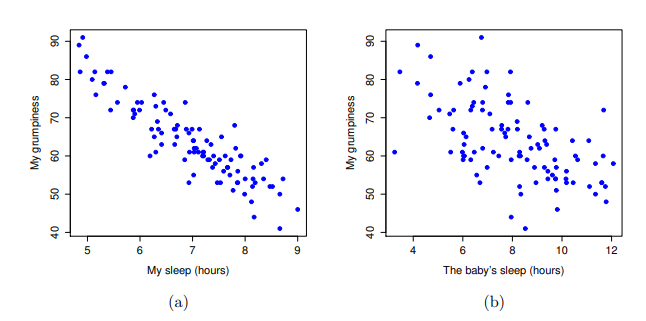
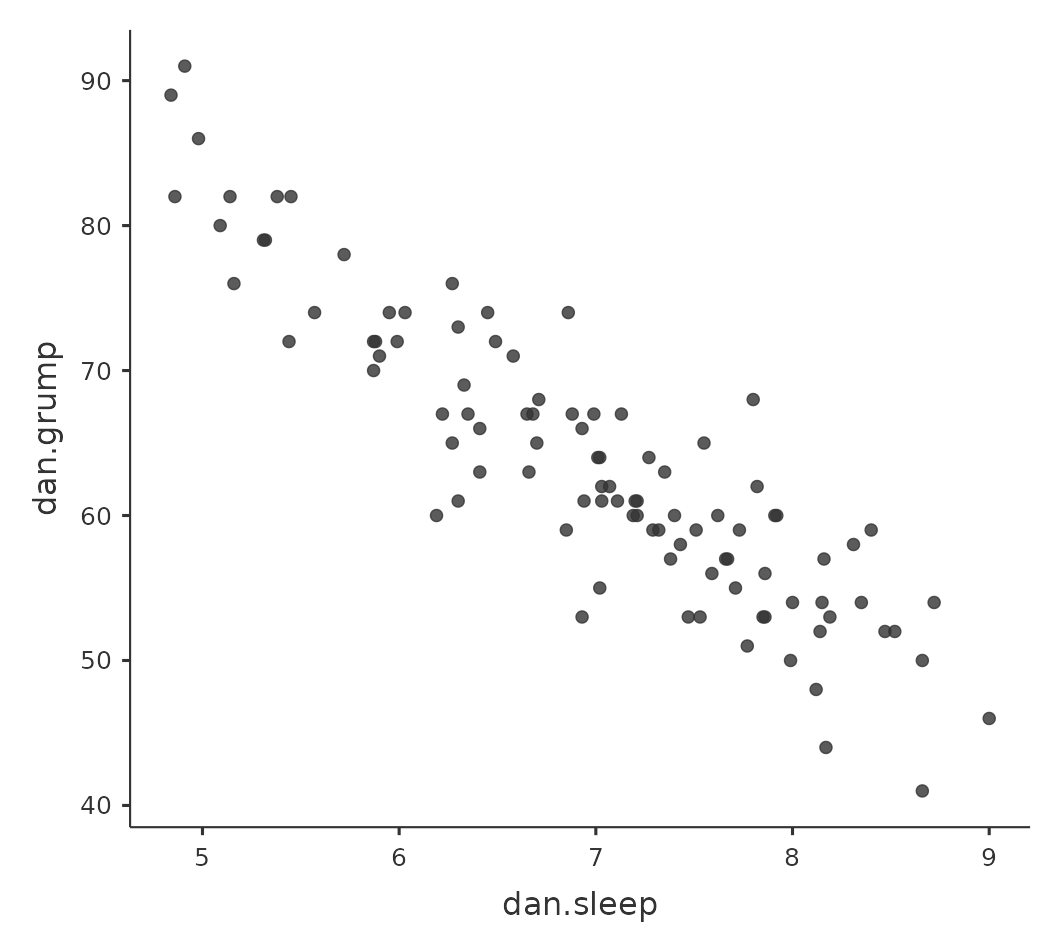
我們可以繪製散佈圖,讓我們能俯瞰兩個變項之間的相關性。雖 然在理想情況下,我們希望能多看到一些資訊。例如,讓我們比較dani.sleep和dani.grump之間的關係( fig-fig10-2 ,左)與baby.sleep和dani.grump之間的關係( fig-fig10-2 ,右)。當我們並排比較這兩份散佈圖,這兩種情況的關係很明顯是同質的:我或者我兒子的睡眠時間越長,我的情緒就越好!不過很明顯的是,dani.sleep和dani.grump之間的關係比baby.sleep和dani.grump之間的關係更強:左圖比右圖更加整齊。直覺來看,如果你想預測我的情緒,知道我兒子睡了多少個小時會有點幫助,但是知道我睡了多少個小時會更有幫助。
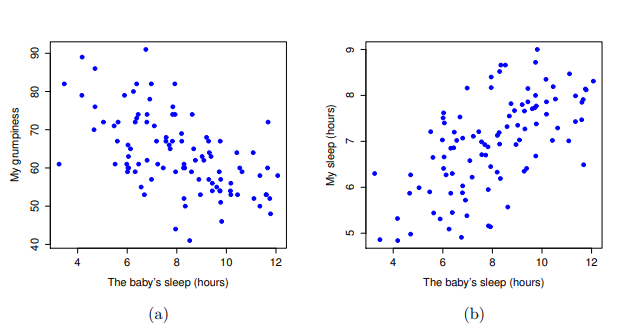
相反地, Figure 10.3 的另外兩個散佈圖告訴我們另一個角度的故事。比較“baby.sleep 與 dani.grump”的散佈圖(左)和“baby.sleep 與 dani.sleep”的散佈圖(右),變項之間的整體關係強度相同,但是方向不同。也就是說,如果我的兒子睡得較長,我也會睡得更多(正相關,右圖),但是他如果睡得更多,我就不會那麼沮喪(負相關,左圖)。
10.1.3 相關係數
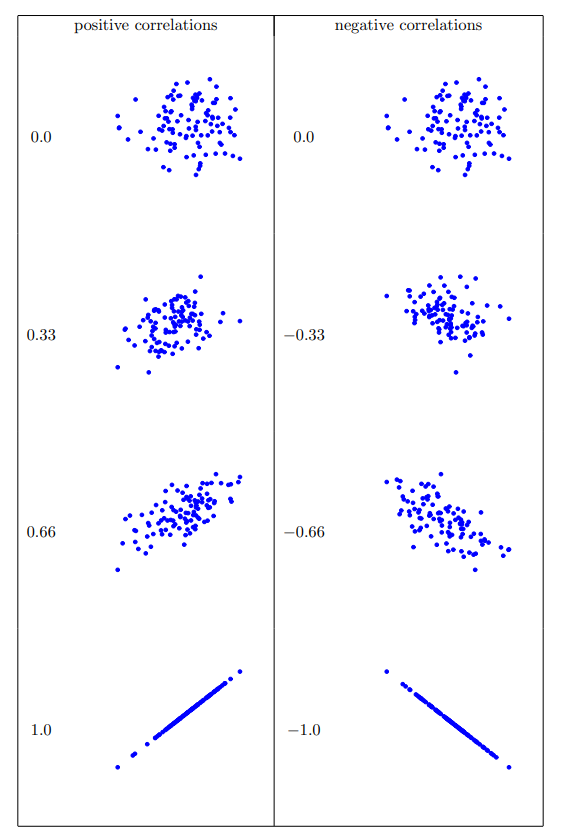
現在我們要進一步延伸上述的概念,也就是正式認識 相關係數(correlation coefficient)。更具體地說,本節主要介紹皮爾森相關係數(Pearson’s correlation),慣例書寫符號是 \(r\)。在下一節,我們會用更精確符號 \(r_{XY}\) ,表示兩個變項 \(X\) 和 \(Y\) 之間的相關係數,值域涵蓋-1到1。當\(r = -1\)時,表示變項之間是完全的負相關;當\(r = 1\)時,表示變項之間是完全的正相關;當\(r = 0\)時,表示變項之間是完全沒有關係。 Figure 10.4 展示幾種不同相關性的散佈圖。
[其他技術細節 4]
標準化共變異數不僅保留前述共變異數的所有優點,而且相關係數r的數值是有意義的: \(r = 1\)代表著完美的正相關,\(r = -1\)代表著完美的負相關。稍後解讀相關係數這一節有更詳細的討論。接著讓我們看一下如何在jamovi中計算相關係數。
10.1.4 相關係數計算實務
只要在jamovi’迴歸’模組選單,選點要計算的相關係數,就能計算所有納入變項對話框的任何兩個變項之間相關係數,如同 Figure 10.5 的示範,沒有出錯的話,報表會輸出’相關係數矩陣’(Correlation Matrix)。
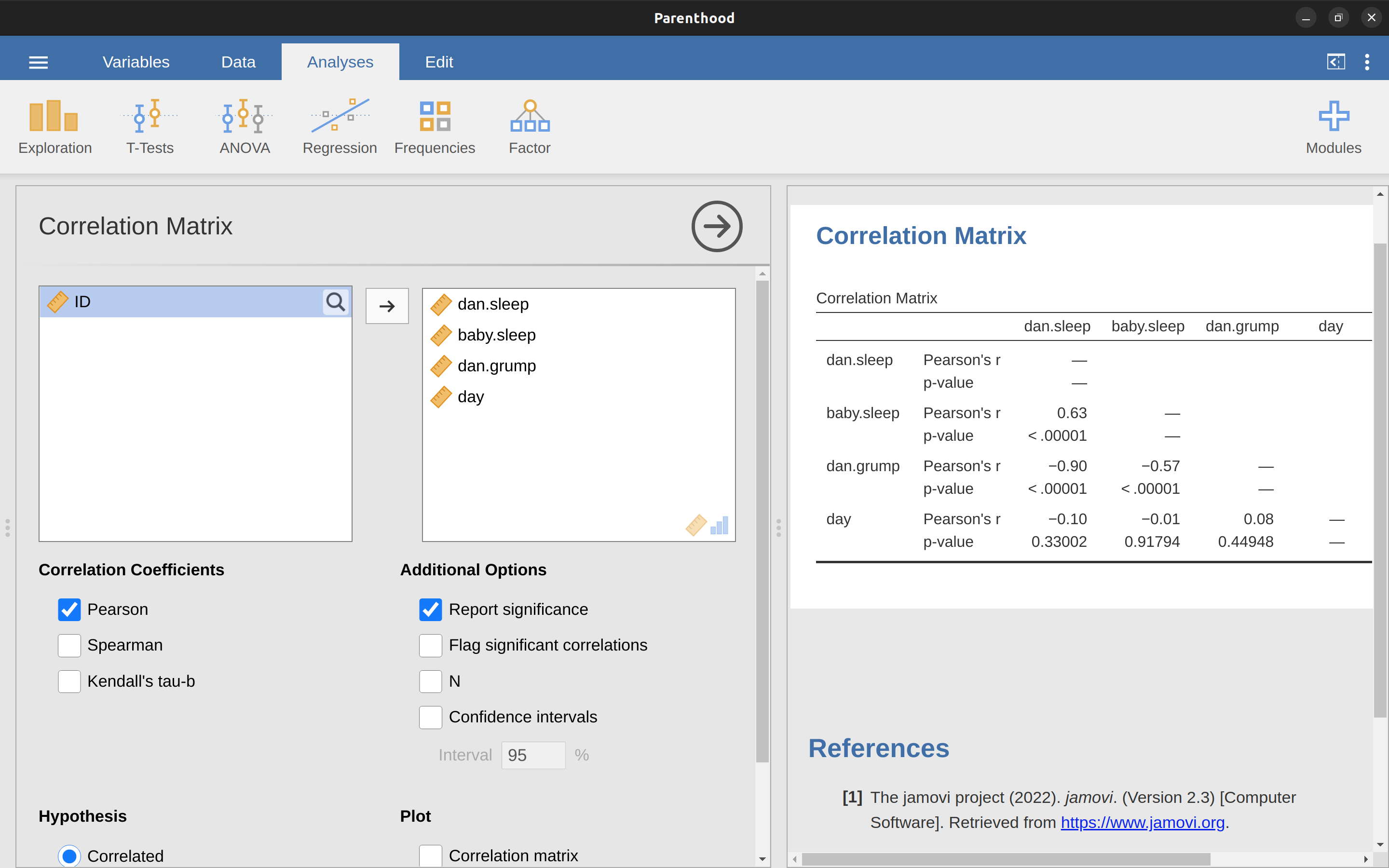
10.1.5 解讀相關係數
在現實世界很少會遇到相關係數為1的狀況。那麼,要如何解讀\(r = 0.4\)的相關性?老實說,這完全取決於你想分析這些資料的目的,以及你的研究領域對於相關係數強度的共識。我(原作者)有一位工程領域的朋友曾經對我說,任何小於\(0.95\)的相關係數都是沒有價值的(我覺得即使對於工程學,他的說法也有點誇張)。在心理學的分析實務,有時應該期望有如此強的相關性。 例如,使用有常模的測驗測試參與者的判斷能力,如果參與者的表現與常模資料的相關性不能達到\(0.9\),任何使用這個測驗預測的理論就會失效5。然而,探討與智力分數有關的因素(例如,檢查時間,反應時間)之間的相關性,如果相關係數超過\(0.3\),已經是非常好的結果。總之,解讀相關係數完全根據解讀的情境。儘管如此,剛開始接觸的同學們可以參考 Table 10.2 的概略式解讀原則。
| 相關係數 | 強度 | 方向 |
|---|---|---|
| -1.0 ~ -0.9 | 非常強 | 負相關 |
| -0.9 ~ -0.7 | 強 | 負相關 |
| -0.7 to -0.4 | 中等 | 負相關 |
| -0.4 ~ -0.2 | 弱 | 負相關 |
| -0.2 ~ 0 | 微弱 | 負相關 |
| 0 ~ 0.2 | 微弱 | 正相關 |
| 0.2 ~ 0.4 | 弱 | 正相關 |
| 0.4 ~ 0.7 | 中等 | 正相關 |
| 0.7 ~ 0.9 | 強 | 正相關 |
| 0.9 ~ 1.0 | 非常強 | 正相關 |
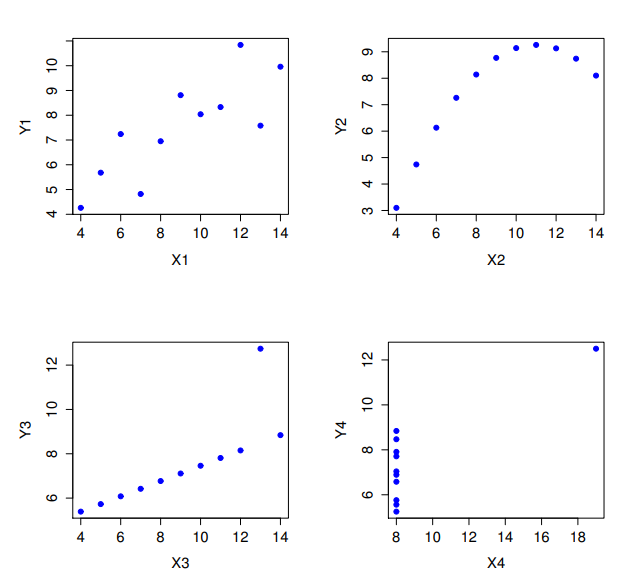
然而,有一件點任何一位統計學教師都會不厭其煩地提醒同學,就是解讀資料變項相關係之前,一定要看散佈圖,一個相關係數可能無法充分表達你要說的意思。統計學中有個經典案例「安斯庫姆四重奏」(Anscombe’s Quartet)(Anscombe, 1973),其中有四個資料集。每個資料集都有兩個變項, \(X\) 與 \(Y\)。四個資料集的 \(X\) 平均值都是 \(9\), \(Y\) 的平均值都是 \(7.5\)。所有 \(X\) 變項的標準差幾乎相同,\(Y\) 變項的標準差也是一致。每種資料集的\(X\) 和 \(Y\) 相關係數均為 \(r = 0.816\)。同學可以打開本書示範資料庫裡的Anscombe資料檔親自驗證。
也許你認為這四個資料集看起來很相似,其實上並非如此。從 Figure 10.6 的散佈圖可以發現,所有四個資料集的\(X\) 和 \(Y\) 變項之間的關係各有千秋。這個案例給我們的教訓是,實務中很多人經常會忘記:「視覺化你的原始數據」(見 Chapter 5 )。
10.1.6 斯皮爾曼等級相關
皮爾森相關係數的用途很多,不過也有一些缺點,尤其是這個係數只是測量兩個變項之間的線性關係強度。換句話說,係數數值是計量整體資料與一條完美直線的趨近程度。當我們想具體表達兩個變項的“關係”時,皮爾森相關係數通常是很好的選擇。但有時並非最佳選項。
線性關係是當一個變項\(X\)的數值增加,也能反映另一個變項\(Y\)的增加。但是兩者關係不是線性的話,皮爾森相關係數就不太合適。例如,準備考試所花的時間和考試成績之間的關係,可能就是這樣的情況。如果一位同學沒有花時間(\(X\))準備一個科目,那麼他排名的成績應該只有0%(\(Y\))。然而,只要一點點努力就會帶來巨大的改善,像是認真上幾堂課並且做筆記就可以學到很多東西,成績排名有可能會提高到35%,而且這是假設沒有做課後復習的情況。然而,想要獲得排名90%的成績,就要比排名55%的成績付出更多努力。也就是說,當我們要分析學習時間和成績的相關係,皮爾森相關係數可能導致錯誤的解讀。
我們用 Figure 10.7 的資料舉例說明,這張散佈圖顯示10名學生在某個課程的讀書時間和考試成績之間的關係。這份虛構的資料怪異之處在於,增加讀書時間總是會提高成績。可能大幅提高,也可能略有提高,但是增加讀書時間絕不會讓成績降低。若是計算這兩個資料變項的皮爾森相關係數,得到的數值為0.91,顯示讀書時間和成績之間有強烈的關係。然而,實際這個分析結果並未充分呈現增加工作時間總是提高成績的關係。儘管我們想要主張兩者的相關性是完全的正相關,但是需要用稍微不同的“關係”來強調,也就是需要另一種方法,能夠呈現這份資料裡完全的次序關係(ordinal relationship)。也就是說,如果第一名學生的讀書時間比二名學生長,那麼我們可以預測第一名學生的成績會更好,而這不是相關係數\(r=0.91\)能表達的。
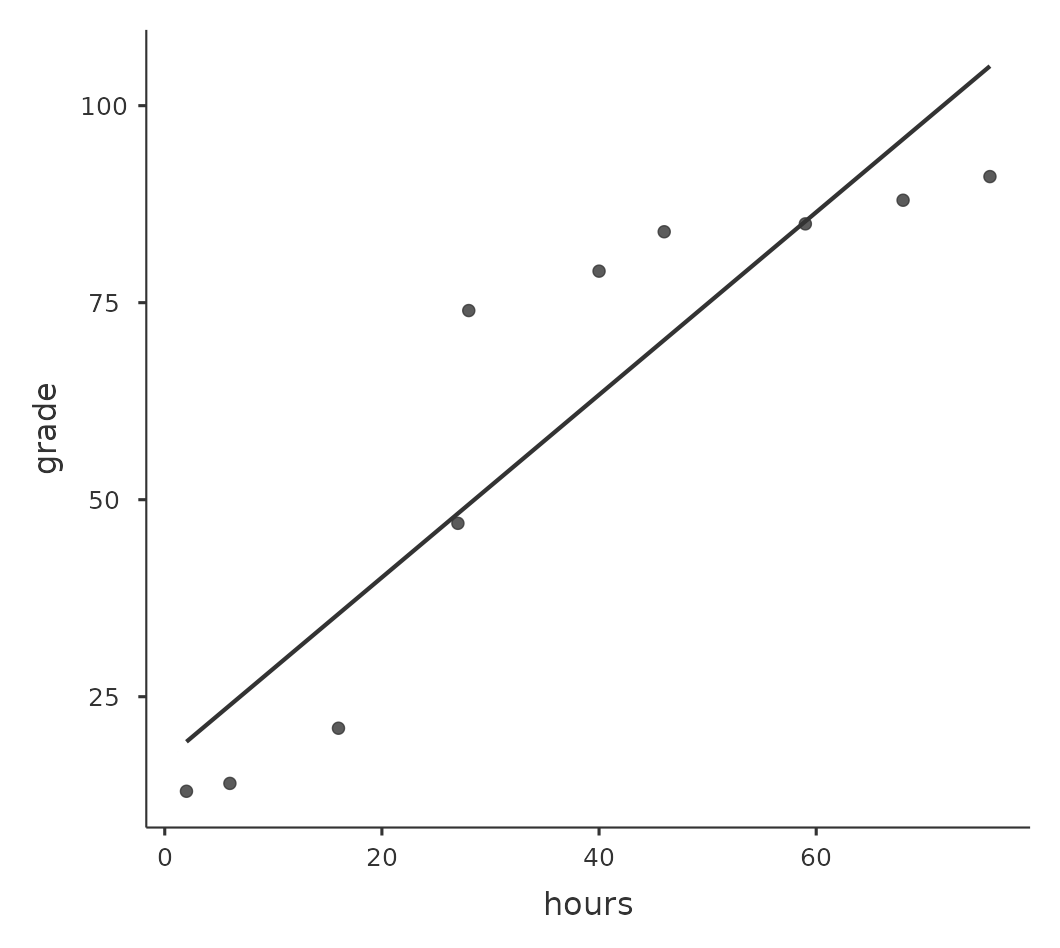
那麼我們要如何解決這個問題呢?其實很容易。如果我們要評估變項之間的次序關係,只需要將資料轉換為次序尺度!所以,接著我們不再用“讀書時間”來衡量學生的努力,而是按照他們的讀書時間長短,將這\(10\)名學生排序。也就是說,學生\(2\)花在讀書的時間最少(\(2\)個小時),所以他獲得了最低的排名(排名=\(1\))。接下來最懶惰的是學生\(4\),整個學期只讀了\(6\)個小時的書,所以他獲得了次低的排名(排名=\(2\))。請注意,在此用“排名=\(1\)”來表示“低排名”。在日常言談裡,多數人使用“排名=\(1\)”表示“最高排名”,而不是“最低排名”。因此,要注意你是用“從最小值到最大值”(即最小值做排名1)排名,還是用“從最大值到最小值”(即最大值做排名1)排名。在這種情況下,我是從最大到最小進行排名的,但是因為很容易忘記設置的方式,所以實務中必須做好紀錄!
好的,讓我們從最努力且最成功的學生開始排名。 Table 10.3 顯示從最努力且最成功的學生排名的次序值。
| 學生編號 | 讀書時間序列 | 成績序列 |
|---|---|---|
| 學生 1 | 10 | 10 |
| 學生 2 | 1 | 1 |
| 學生 3 | 5 | 5 |
| 學生 4 | 8 | 8 |
| 學生 5 | 9 | 9 |
| 學生 6 | 6 | 6 |
| 學生 7 | 7 | 7 |
| 學生 8 | 3 | 3 |
| 學生 9 | 4 | 4 |
| 學生 10 | 2 | 2 |
有意思的是,兩個變項的排名是相同的。投入最多時間的學生得到了最好的成績,投入最少時間的學生得到了最差的成績。由於個變項的排名是相同的,只要計算皮爾森相關係數,就會得到一個完美的相關係數1.0。
至此我們等於重新發現 斯皮爾曼等級相關(Spearman’s rank order correlation),通常用符號 \(\rho\) 表示,以區分皮爾森相關係數\(r\)。我們可以在jamovi的“相關矩陣”選單選擇“Spearman”,計算斯皮爾曼等級相關係數。6
10.2 散佈圖
散佈圖是一種簡單但有效的視覺化工具,用於具現兩個變項之間的關係,就像相關這一節所展示的圖表。通常提到“散佈圖”這個術語時,指的是具體的視覺化結果。在散佈圖中,每個觀察值都是對應一個資料點。一個點的水平位置表示一個變項的觀察值,垂直位置表示觀察值在另一個變項的數值。在許多使用情境,我們對於變項間的因果關係並沒有清晰的看法(例如,A是否引起B,還是B引起A,還是其他變項C控制A和B)。若是這樣,x軸和y軸上代表那個變項並不重要。然而在許多情境,研究者對於那個變項最有可能是原因或結果,會有一個相當明確的想法,或者對於何者為因至少有一些懷疑。若是這樣,用x軸代表原因的自變項,用y軸代表效應的應變項是一種傳統的繪圖規範。了解這樣的規範,讓我們來看一下如何合理運用jamovi繪製散佈圖,同樣使用在相關這一節做為示範的資料集(parenthood.csv)。
假定我的目標是繪製一個顯示我睡眠時間(dani.sleep)與隔天沮喪程度(dani.grump)兩個變項關係的散佈圖,我們有兩種不同的方法使用jamovi得到我們想要的圖。第一種方法是設定’Regression’ - ‘Correlation Matrix’選單下方的’Plot’選項,這樣可以得到如圖 Figure 10.8 的結果。請注意,jamovi會繪製一條通過資料點的直線,稍後在認識線性迴歸模型這一節進一步說明。以這種方法繪製散佈圖也能繪製’變項密度’,這個選項會添加一條密度曲線,顯示每個變項的資料分佈狀況。
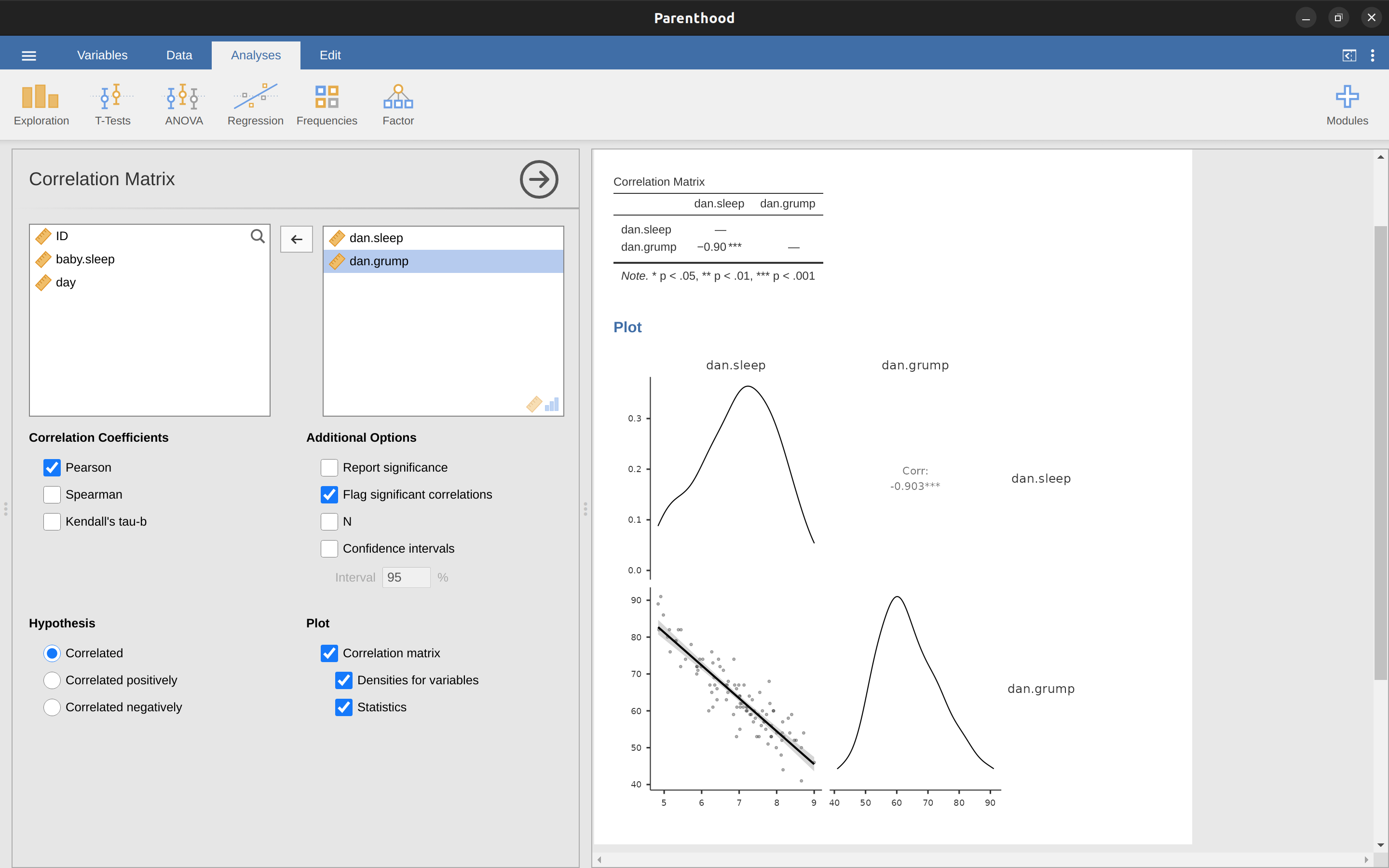
第二種方法是使用jamovi的附加模組之一scatr,只要點擊jamovi介面右上角的那個大「\(+\)」,在jamovi模組庫裡找到scatr,然後點擊「install」進行安裝。安裝成功後,在「Exploration」的選單下方會多出新的「Scatterplot」選項。這種方法繪製的散佈圖和第一種方法不大一樣,如同 Figure 10.9 所顯示,但是透露的訊息是一樣的。
10.2.1 更多解讀散佈圖的方法
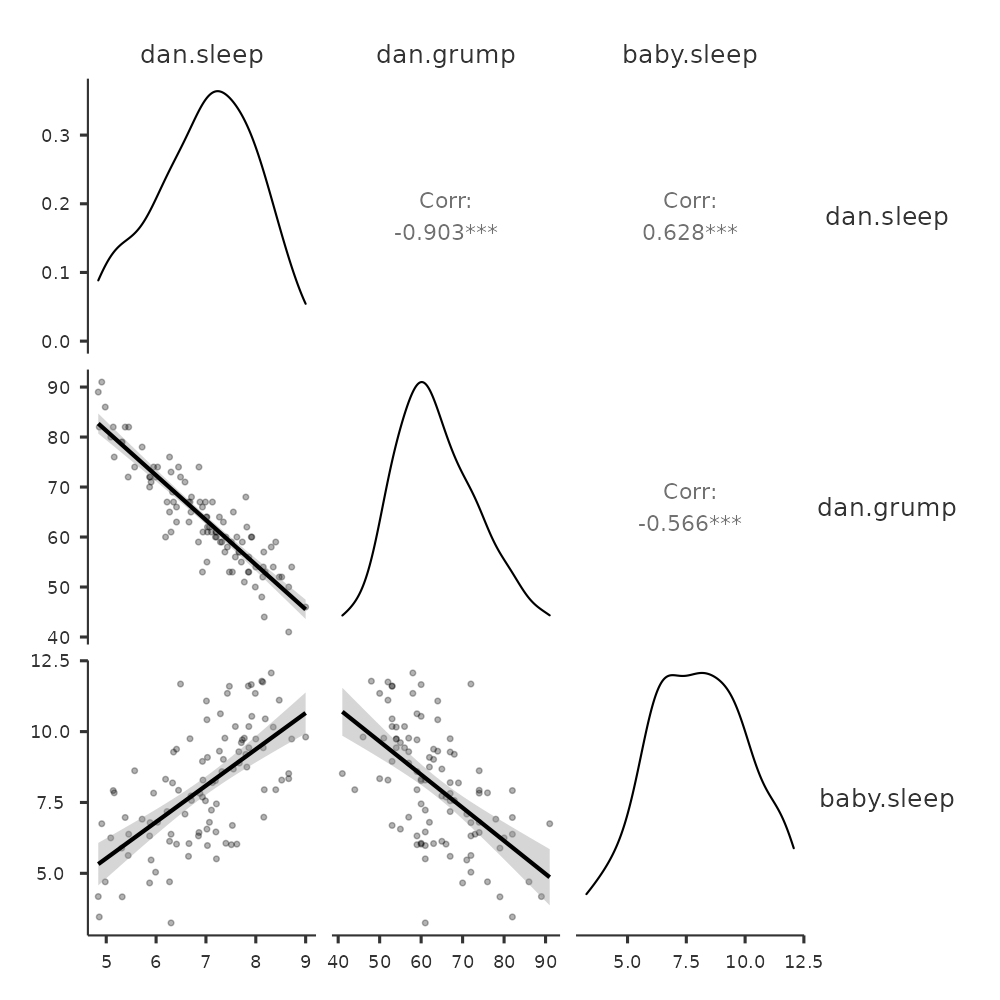
通常我們會需要查看多個變項之間的關係,可以在 jamovi 的 ‘Correlation Matrix’選單下方的’Plot’ 選項,勾選繪制散佈圖矩陣。只要加入另一個變項到要變項列表,例如 baby.sleep,jamovi 就會生成一個散佈圖矩陣,如同 Figure 10.10 的示範。
10.3 認識線性迴歸模型
我們可以將線性迴歸模型理解為稍微複雜一點的皮爾森相關係數分析程序(請見相關這一節),稍後我們會看到,迴歸模型是用途更廣泛的統計方法。
由於迴歸模型的基本觀念與相關係數緊密相關,以下同樣使用parenthood.csv資料集進行介紹及示範。回想一下,我們分析這個資料集的目的是,找出我(原作者Dani)為什麼總是非常沮喪的原因,而我的研究假設是我沒有得到足夠的睡眠。所以畫了一些散佈圖,檢示實際睡眠時間與隔天沮喪程度之間的關係,就像 Figure 10.9 展示的散佈圖,兩者之間的相關係數達到\(r=-0.90\)。但是,我想描述的變項間關係更像 Figure 10.11 (a) ,也就是有一條直線穿過資料點的中間。這條直線的統計學術語是迴歸線。請注意,由於我不是統計新手,因此畫出的迴歸線一定會穿過資料散佈區域的中間地帶,絕不會認為是像 Figure 10.11 (b) 的樣子。
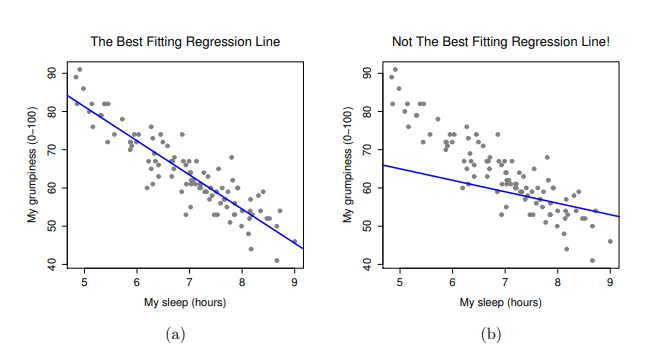
確認能解讀變項間關係的迴歸線,並不需要什麼厲害的技巧。 Figure 10.11 (b)的那條線與資料的適合度(fittedness)並不高,用來解讀資料沒有太大的意義,對吧?迴歸線能很直覺地呈現變項間的關係,若是再應用迴歸線的數學理論解讀資料,會變成非常強大的分析工具。我們複習一下高中數學,一條直線的公式可以寫成這樣的等式:
\[y=a+bx\]
至少幾十年前澳洲的高中數學課是這樣教的。兩個資料變項用 \(x\) 和 \(y\)代表,搭配兩個係數 \(a\) 和 \(b\) 形成變項之間的等價性。7係數 \(a\) 代表迴歸線的截距,係數 \(b\) 代表迴歸線的斜率。努力回憶一下高中曾學過的內容(很抱歉,某些讀者也許已經離開高中校園很了),記得截距被解釋為“當 \(x=0\) 時得到的 \(y\) 值”。同樣地,斜率 \(b\) 若為正值,代表增加 \(x\) 的數值一個單位, \(y\) 值會增加 \(b\) 個單位;而斜率 \(b\) 若為負值,則代表 \(y\) 值會下降而不是上升。啊,是的,我們現在全都回想起來了。現在我們的記憶已經回來,所以自然會發現可以使用完全相同的公式計算迴歸線。如果 \(Y\) 是預測變項(依變項),\(X\) 是應變項(自變項),那麼描述示範資料的迴歸線等式就會像是這樣:
\[\hat{Y}_i=b_0+b_1X_i\]
嗯,這看起來這跟曾在高中教科書看到的公式一模一樣,只是多了些花俏的下標符號,讓我們來了解這些符號的意思。首先,請注意我使用 \(X_i\) 和 \(Y_i\),而不是 \(X\) 和 \(Y\),這是因為有下標符號的代數通常代表實際的資料。在這個公式裡,\(X_i\) 代表第 i 個觀察值的預測變項的值(例如我在第 i 天紀錄的睡眠時間),而 \(Y_i\) 則是對應的應變項數值(例如我當天的沮喪程度)。雖然公式裡沒有明確說明,但我們假設這個公式對資料集裡的所有觀察值都通用(即 i 對應所有 觀察日數)。其次,請注意我寫的是 \(\hat{Y}_i\) 而不是 \(Y_i\),這是因為我們要區分實際數值 \(Y_i\) 與被預測數值 \(\hat{Y}_i\)(也就是經由迴歸線預測的數值)。第三,我將代表係數的符號從 a 和 b 改成 \(b_0\) 和 \(b_1\),這是統計學家喜歡呈現迴歸模型的方式。我不知道為什麼他們選擇用 b 這個字母,但這就是統計學的慣例。無論如何,\(b_0\) 總是代表截距,\(b_1\) 則是代表斜率。
跟上來的話就很好。接著我們會注意到,無論是好的迴歸線還是壞的迴歸線,資料都是不完美地落在迴歸線。換句話說,實際數值\(Y_i\)不完全等於迴歸模型預測的數值\(\hat{Y}_i\)。由於統計學家喜歡給一切符號冠上字母、名稱和數字,讓我們稱呼模型預測的數值與實際數值之間的差異為殘差(Residuals),代表符號為\(\epsilon_i\)。8 使用數學公式表示的話,殘差可被定義為:
\[\epsilon_i=Y_i-\hat{Y}_i\]
接著我們就可以寫出完整的線性迴歸模型:
\[Y_i=b_0+b_1X_i+\epsilon_i\]
10.4 線性迴歸模型的參數估計
好的,現在讓我們重新繪製散佈圖,這次會添加一些線條顯示所有觀察值的殘差。當迴歸線的適合度(fittedness)最佳時,每個殘差數值(實心黑線的長度)看起來都非常小且接近,如同 Figure 10.12 (a) ,但是當迴歸線的適合度不夠好,每個殘差之間的差異就會非常大,可以從 Figure 10.12 (b)看到這樣的差別。嗯,也許在尋找一條最好的迴歸模型時,我們會希望得到儘可能小的殘差。是的,這確實有道理。在統計實務,我們可以說「最適合」的迴歸線是具有所有殘差最小的線。或者更好的說法是,因為統計學家似乎喜歡將所有數值都用平方(sqaured)處理,也就是說:
以資料估計的迴歸係數 \(\hat{b}_0\) 和 \(\hat{b}_1\) 是殘差平方和最小得到時得到的估計值,我們可以兩者的公式展開寫成 \(\sum_i (Y_i - \hat{Y}_i)^2\) 與 \(\sum_i \epsilon_i^2\) 。
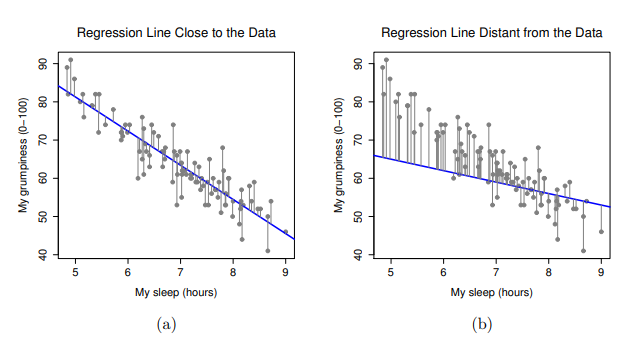
是的沒錯,這樣說明起來更有學問一些。而且我將這段話縮排,表示這樣說可能是正確的解答。既然這是正確解答,那麼要值得注意的是,迴歸線的係數都是估計值(請復習 Chapter 8 ,使用點估計方法猜測一個母群的參數!),這也是為什麼我要在代表係數的符號上頭加個小帽子 ^ ,區別會放在報告的是\(\hat{b}_0\)和\(\hat{b}_1\),而不是 \(b_0\) 和 \(b_1\)。最後,我還要指出,由於實際上有許多方法來估計迴歸模型,這一節說明的估計方法正式名稱是普通最小平方法(Ordinary Least Squares,OLS)。
至此,我們已經得到「最佳」迴歸係數 \(\hat{b}_0\) 和 \(\hat{b}_1\) 的具體定義。下一個問題自然是:如果最佳迴歸係數是那些符合最小化殘差平方和的係數,我們要如何算出這些數值呢?實際上,這個問題的答案比較複雜,並且無法幫助你理解迴歸的邏輯。9這一次,我放過各位同學,直接介紹 jamovi 操作方法,瑣碎的讓jamovi來處理。
10.4.1 實作線性迴歸模型
以下是用parenthood.csv 資料檔案執行線性迴歸分析的步驟,請打開 jamovi 的 ‘Regression’ - ‘Linear Regression’ 選單 。接著,將 dani.grump 指定為 ‘Dependent Variable’,dani.sleep 輸入到 ‘Covariates’ 對話框。報表介面將出現如 Figure 10.13 的結果,結果顯示截距 \(\hat{b}_0 = 125.96\) 和斜率 \(\hat{b}_1 = -8.94\)。換言之, Figure 10.11 的最適合迴歸線的公式為:
\[\hat{Y}_i=125.96+(-8.94 X_i)\]
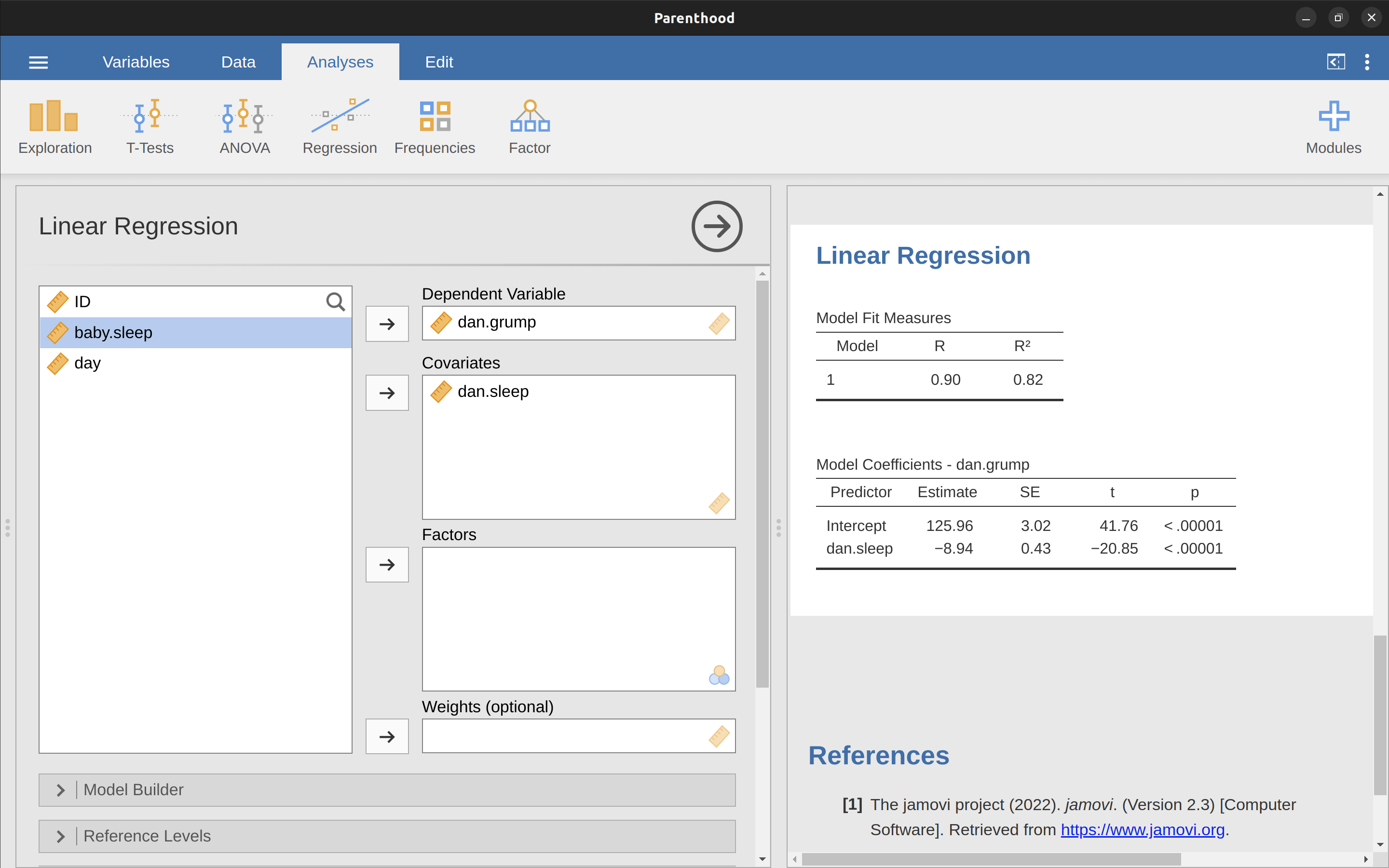
10.4.2 解讀線性迴歸模型參數估計
最後要知道的是如何解釋這些係數。讓我們從 \(\hat{b}_1\) 開始,也就是斜率。回想一下斜率的定義,\(\hat{b}_1=-8.94\) 代表將 \(X_i\) 增加 1, \(Y_i\) 就會減少 8.94。換言之,多睡一個小時的話,我的心情就會改善,我的沮喪程度就會降低 8.94 。那麼截距呢?由於 \(\hat{b}_0\) 代表「當 \(X_i\) 為 0 時 \(Y_i\) 的期望值」,這就是說如果我一夜都沒睡 (\(X_i = 0\)),我的沮喪程度就會瘋狂升高到不敢想像的數值 (\(Y_i = 125.96\))。我想我最好避免這種狀況。
- 還有關於等級資料(Rank data)的迴歸分析,請參考線性模型的學習取向的相關與線性迴歸這一節。
- 以下 Section 10.5 、 Section 10.10 以及 Section 10.11 等三個小單元,是屬於傳統高等統計課程的範圍,其他單元在多數教科書被劃分為基礎統計的範圍。不過接下來的單元裡原作者都是混合一元迴歸與多元迴歸的示範案例,譯者將在屬於多元迴歸的小單元開頭明示譯註,提供使用這本電子書學習的學生與教學的老師,根據自身的學習目標決定如何運用該節內容。
10.5 多元線性迴歸
譯註:這個單元全部內容都是談多元迴歸,內容文字編修排在本書最後階段進行。
到目前為止,我們討論過的簡單線性迴歸模型假設只有一個您感興趣的預測變項,在這種情況下是dani.sleep。事實上,在這一點上,我們談到的每一個統計工具都假設您的分析使用一個預測變項和一個結果變項。然而,在許多(也許是大多數)研究項目中,實際上有多個您想要研究的預測變項。如果是這樣,將線性迴歸框架擴展到包含多個預測變項可能會很好。也許某種多元迴歸模型將會合適?
多元迴歸在概念上非常簡單。我們所做的就是在我們的迴歸方程中添加更多項。假設我們對兩個變項感興趣;也許我們想要使用dani.sleep和baby.sleep來預測dani.grump變項。像以前一樣,我們用\(Y_{i}\)表示第i天的煩躁程度。但現在我們有兩個$ X \(變項:第一個對應我得到的睡眠量,第二個對應我兒子得到的睡眠量。所以我們用\)X_{i1}\(表示第i天我睡的時間,\)X_{i2}$表示那一天嬰兒睡的時間。如果是這樣,那麼我們可以這樣寫我們的迴歸模型:
\[Y_i=b_0+b_1X_{i1}+b_2X_{i2}+\epsilon_i\]
像以前一樣,\(\epsilon_i\)是與第i個觀察值相關的殘差,\(\epsilon_i = Y_i - \hat{Y}_i\)。在這個模型中,我們現在有三個需要估計的係數:b0是截距,b1是與我的睡眠相關的係數,b2是與我兒子的睡眠相關的係數。然而,儘管需要估計的係數數量有所改變,估計工作的基本思路沒有改變:我們的估計係數\(\hat{b}_0\)、\(\hat{b}_1\)和\(\hat{b}_2\) 是那些使殘差平方和最小化的係數。
10.5.1 jamovi實務示範
在jamovi中,多元迴歸與簡單迴歸無異。我們所要做的就是在jamovi中的’協變項’框中添加更多變項。例如,如果我們想要使用dani.sleep和baby.sleep作為預測變項來解釋為什麼我如此煩躁,那麼將baby.sleep移動到與dani.sleep相鄰的’協變項’框中。默認情況下,jamovi假設該模型應該包括一個截距。這次我們得到的係數顯示在 Table 10.4 中。
| 截距 | 老爸睡眠小時數 | 小嬰兒睡眠小時數 |
|---|---|---|
| 125.97 | -8.95 | 0.01 |
與dani.sleep相關的係數相當大,表明每失去一個小時的睡眠,我會變得更加煩躁。然而,baby.sleep的係數非常小,表明我的兒子睡多少其實無關緊要。就我的煩躁程度而言,重要的是我睡多少。為了讓您對這個多元迴歸模型有所了解,?fig-fig10-14顯示了一個三維圖,繪製了所有三個變項以及迴歸模型本身。
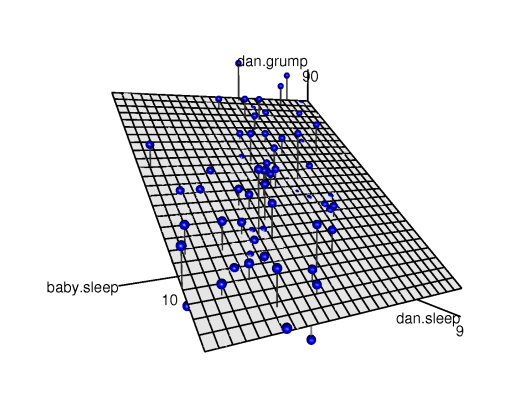
[附加技術細節10]
10.6 迴歸模型的適合度
現在我們知道如何估計線性迴歸模型的係數。問題是,我們還不知道這個迴歸模型是否有效。例如,根據一號模型,多睡一小時我(原作者)的情緒會大大改善,但這可能只是廢話。請記住,迴歸模型只是生成個人情緒的預測值 \(\hat{Y}_i\),實際的情緒量測值則是 \(Y_i\)。如果兩種數值非常接近,表示迴歸模型非常適合預測我的情緒變化。如果兩種數值差異很大,那麼這個模型就並不太適合用來預測我的情緒變化。
10.6.1 \(R^2\)
我們再次引用一些數學知識解釋如何評估模型的適合度。首先來認識殘差平方和
\[SS_{res}=\sum_i (Y_i-\hat{Y_i})^2\]
實務上會期望殘差平方和越小越好。具體地說,殘差平方和佔總變異平方和的比例越小越好
\[SS_{tot}=\sum_i(Y_i-\bar{Y})^2\]
談到這裡,我們可以逐步計算這些數值,不過不是用手算。而是使用像是Excel或其他試算表軟體。在Excel中打開parenthood.csv這份檔案,再另存新檔為parenthood rsquared.xls就能完成計算。計算步驟第一步是計算 \(\hat{Y}\) 值,按照以下步驟,我們可以得到以我的睡眠時間預測情緒的簡單迴歸模型:
- 使用公式
= 125.97 + (-8.94 * dani.sleep)創建新欄位Y.pred。 - 創建新欄位
(Y-Y.pred)\^2,使用公式= (dani.grump - Y.pred)\^2計算SS(resid)。 - 在
(Y-Y.pred)\^2的最後一列使用公式sum( ( Y-Y.pred)\^2 )計算這些值的總和。 - 在
dani.grump的最後一列,計算dani.grump的平均值(留意Excel的函數是’AVERAGE’而不是’mean’)。 - 創建新欄位
(Y - mean(Y))\^2 ),使用公式= (dani.grump - AVERAGE(dani.grump))^2。 - 在
(Y - mean(Y))\^2 )最後一列,使用= sum( (Y - mean(Y))^2 )計算總和。 - 在一個空白儲存格中輸入
= 1 - (SS(resid) / SS(tot) ),計算R.squared。
至此我們算出 \(R^2\) 的數值 = 0.8161018。\(R^2\) 在有些教科書裡被稱呼為決定係數11,這個名稱有一個簡單的解釋:預測變項總變異解釋依變項總變異的比例。因此,在這裡得到的 \(R^2 = .816\) 代表預測變項(my.sleep)解釋依變項(my.grump)總變異的81.6%。
想當然而,如果同學想計算迴歸模型的 \(R^2\) ,實際上不需要自己用 Excel 計算。稍後在 Section 10.7.3 用 jamovi 執行假設檢定這一節,同學會看到只要在模組選單裡勾選指定選項即可。現在,讓我們暫時擱置計算問題,我想談談 \(R^2\) 的另一個性質。
10.6.2 迴歸與相關的關聯
現在可以重新回顧在這一章開始,我說到迴歸與相關基本上是同一回事。在相關的小單元,我們用符號 \(r\) 表示皮爾森相關。那麼皮爾森相關係數 \(r\) 和線性迴歸的 \(R^2\) 有存在某種關係嗎?當然有:只要將相關係數開平方, \(r^2\) 與只有一個預測變項的線性迴歸 \(R^2\) 數值是相同的。換句話說,計算皮爾森相關與計算僅有一個預測變項的線性迴歸模型基本上是相同的。
10.6.3 校正後 \(R^2\)
譯註:只有分析多元迴歸的場景,才要了解校正後 \(R^2\)。
在繼續到下個單元之前,我最後要指出的是,統計實務通常會報告一個稱為“校正後 \(R^2\) ”的計量值。計算及報告校正後 \(R^2\) 值的理由是,到將兩個以上預測變項添加到模型中,總是會增加(或至少不降低) \(R^2\) 。
[額外技術細節12]
校正的目的是為了處理自由度。校正後 \(R^2\) 的主用用途是,往模型添加更多預測變後,只有能提高模型預測能力的新變項,才會顯著增加校正後 \(R^2\)的數值。然而,校正後 \(R^2\)就無法像一開始的 \(R^2\) 那樣的直接解釋。據我所知,調整後的 \(R^2\) 沒有任何相等意義的解釋。
那麼統計實務中應該要報告 \(R^2\) 還是校正後 \(R^2\)?這可能是因人而異。如果同學比較想解釋報告裡的數值,那麼 \(R^2\) 較好。如果在乎校正模型的預測偏差,那麼校正後 \(R^2\) 可能比較好。就我(原作者)自己而言,我更喜歡 \(R^2\),因為我覺得最重要的是能夠解釋模型預測能力的計量。此外,我們將在 Section 10.7 迴歸模型的假設檢定這個小單元看到,如果想知道添加預測變項後增加的 \(R^2\) 是由於機遇還是因為模型預測能力真的改善了,那麼我們可以用假設檢定來做判斷。
10.7 迴歸模型的假設檢定
至此我們已經學到什麼是迴歸模型,如何估計迴歸模型的係數,以及量化模型預測效能的方法(順便說一下,相關係數與迴歸係數就是一種效果量的估計值)。接下來學習課題的是假設檢定。我們要學習兩種不同(但相關)的假設檢定:一種是檢驗包合所有預測變項的迴歸模型是否顯著優於只有截距的模型,另一種是我們檢驗只有單一預測變項的模型,迴歸係數是否顯著不等於零。
10.7.1 檢定所有預測變項的模型
譯註:只有分析多元迴歸的場景,才要進行這種檢定。內容文字編修排在本書最後階段進行。
好吧,假設你已經估計了你的迴歸模型。你可能會嘗試的第一個假設檢定是虛無假設,即預測變項和結果之間沒有關係,而對立假設是數據的分佈完全符合迴歸模型的預測。
[額外的技術細節13]
我們將在 Chapter 12 中看到更多 F 統計量,但目前只需知道我們可以將較大的 F 值解釋為虛無假設與對立假設相比表現不佳。過一會兒,我將向您展示如何用 jamovi 輕鬆進行檢驗,但首先讓我們看一下單個迴歸係數的檢驗。
10.7.2 單一迴歸係數的檢定
前一節介紹的 F 檢定對於檢查整個線性模型是否優於隨機截距模型很有用。如果您的迴歸模型並未在 F 檢定看到顯著結果,那麼這套迴歸模型可能不是有效解讀資料的好模型(或者是要分析的資料可能並不夠好)。然而,儘管這個檢定失敗是表示模型是否可用的明顯指標,但是通過檢定(也就是拒絕虛無假設)並不表示這個模型是真的好模型!也許同學會想知道為什麼?答案在前面 Section 10.5 多元線性迴歸 已經有討論過的。
注意一下 Table 10.4 的數值,與 dani.sleep 變項的迴歸係數估計數值(\(-8.95\))相比,baby.sleep 變項的迴歸係數估計數值非常小(\(0.01\))。考慮到這兩個變項的度量尺度都是一樣的(都是以“睡眠小時數”),我發現這很有啟發性。其實我看了 Table 10.4 就有想到,要預測我的沮喪程度,真正重要的變項應該只有我自己的睡眠時間長度。我們可以使用之前學到的假設檢定方法,確認我的懷疑14。我們想檢定的虛無假設是設定迴歸係數為零(\(b = 0\)),與迴歸係數不是零(\(b \neq 0\))的對立假設進行檢定。也就是說:
\[H_0:b=0\] \[H_1:b \neq 0\]
這個檢定要如何進行?好吧,如果還記得中心極限定理,同學可能會猜到迴歸係數的估計值\(\hat{b}\)是一種取樣分佈,而且是以 \(b\) 為中心的常態分佈。這表示如果虛無假設是真的,那麼\(\hat{b}\)的取樣分佈平均值為零並且標準差是未知數。假設我們可以找到迴歸係數的標準誤差估計值,\(se(\hat{b})\),那麼我們就很幸運。這正好可以用 Chapter 11 介紹的單一樣本 t 檢定處理。現在可以定義以下的 t 統計值
\[t=\frac{\hat{b}}{SE(\hat{b})}\]
這裡不詳細說明為什麼能這樣做的原因,但在這種狀況,自由度是 \(df = N - K - 1\)。令初學者厭煩的通常是,迴歸係數的標準誤估計值,\(se(\hat{b})\),並不像 Chapter 11 介紹的單一樣本 t 檢定的平均值標準誤那樣容易計算。真實的公式長得有點醜陋,看起來並不那麼平易近人。15 對於我們要真正完成的目標,只需要知道迴歸係數估計值的標準誤取決於預測變項和依變項,並且要留意有沒有違反變異數相等的適用條件 (稍後 Section 10.9 就會討論)。
無論如何,這個t統計值可以按照 Chapter 11 介紹的檢定方法解釋結果。若是設定做雙尾檢定(也就是說,你不在乎是b > 0還是b < 0),那麼極端的t值(即遠小於零或遠大於零的值)表示你應該拒絕虛無假設。
10.7.3 用 jamovi 執行假設檢定
要計算以上介紹的統計量數,只需要在jamovi迴歸模組選單勾選對應的選項。要選擇的選項如同 Figure 10.15 的示範,會得到一系列有用的報表輸出。
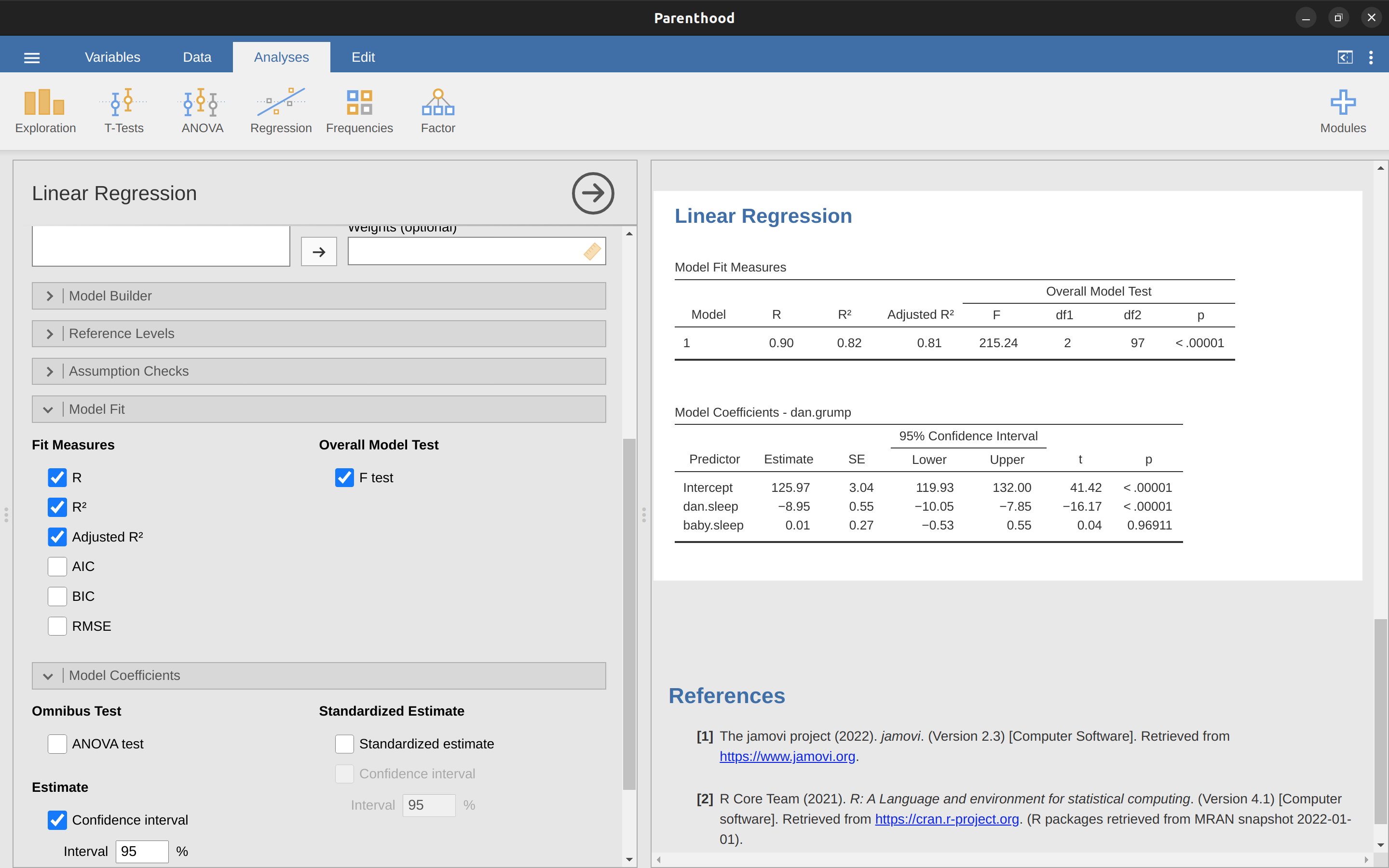
在jamovi分析結果的“模型係數”表格(Model Coefficients)顯示迴歸模型的係數。此表中的每一行都是對應迴歸模型的其中一個係數。第一行是截距,後面每一行是每個預測變項的檢定結果。每一列標示各種統計訊息。第一列是\(b\)的實際估計值(例如,截距為\(125.97\),預測變項dani.sleep 為\(-8.95\))。第二列是標準誤的估計值\(\hat{\sigma}_b\)。第三和第四列是關於係數估計值的95%信賴區間的下限和上限(稍後對此有更多說明)。第五列是t統計值,值得注意的是,在這個表格中,\(t=\frac{\hat{b}} {se({\hat{b}})}\)每次分析結果都是成立的。最後一列呈現這些檢定結果的p值。16
模型係數表唯一沒有列出的是t檢定的自由度,不過其值始終是\(N - K - 1\),並且輸出到報表標題後的“模型適合度度量”(Model Fit Measures)表格中17。從這個表格中,我們可以看到模型的表現顯著優於機會水平(\(F(2,97) = 215.24, p< .001\)),其實這並不奇怪:\(R^2 = .81\)值表示迴歸模型能解釋依變項變異量的\(81\%\)(調整後的\(R^2\)為\(82\%\) )。然而,當我們回顧每個個別係數的t檢定時,我們有相當有力的證據表明baby.sleep變項沒有顯著效果。這個模型的主要預測效力都是來由dani.sleep變項。綜合這些結果,我們可以結論這個多元迴歸模型實際上並不是能有效解 資料的模型,最好的模型應該排除baby.sleep這個預測變項。換句話說,開始的簡單迴歸模型是更好的模型。
10.8 迴歸係數的估計值
在討論線性迴歸的適用條件,以及如何檢查一種模型是否滿足條件之前,這裡先簡單討論兩個與迴歸係數有關的主題。首先是如何計算迴歸係數的信賴區間。然後是如何確定哪個預測變項最重要。
10.8.1 迴歸係數的信賴區間
就像任何人口變項一樣,迴歸係數b無法從樣本資料精確地估算出來;這就是為什麼需要使用假設檢定的一部分原因。有鑑於此,信賴區間能夠呈現捕捉\(b\)真實數值的不確定性,是非常有用的工具。這在嘗試找出變項\(X\)與變項\(Y\)之間的關係強度的研究問題尤其有用,因為在這些研究裡,主要關注的是迴歸權重\(b\)(regression weight)。
[額外技術細節18]
在jamovi的操作界面,我們可以指定“95%信賴區間”,如 Figure 10.15 的示範,如果想要更嚴謹的話,我們可以輕鬆選擇另一種區間,例如“99%信賴區間”。
10.8.2 標準化迴歸係數的計算方法
有經驗的使用者可能還會計算“標準化”迴歸係數,通常報告中用\(\beta\)表示。標準化係數的基本原理是:在很多情況下,每個變項的測量尺度是不一樣的。例如,如果有個迴歸模型要探討受教育程度(受教育年數)和收入作為預測變項,來預測受測者的智力測驗得分。顯然,受教育程度和收入的計量尺度是不相同的。一般人的教育年限可能只有10多年,而收入差距可能高達10,000美元(或更多)。計量單位對迴歸係數有很大影響,只有預測變項和依變項的計量單位一致時,迴歸係數才具有意義,否則比較不同預測變項的迴歸係數將會非常困難。然而,有時我們希望能比較不同變項的係數。具體來說,研究者最想找到那些預測變項與依變項之間相關性最強力的標準衡量指標,這就是為什麼有標準化迴歸係數。
標準化迴歸係數的思路很簡單;如果在執行迴歸分析之前將所有變項轉換為z分數,標準化係數就是您會得到的係數。19這裡的想法是,將所有預測變項數值轉換為z分數,使得迴歸模型的生成的機率分佈具有可對應的比例,進而消除不同尺度的變項產生的問題。無論變項的原始尺度是什麼,\(\beta\)值為1都代表增加預測變項的1個標準差,就是導致依變項的對應數值增加1個標準差。因此,如果預測變項A的\(\beta\)絕對值大於預測變項B的\(\beta\),研究者至少能主張預測變項A與依變項的相關性更強。值得小心的是,對於所有變項變異基本相同的這個條件 ,其實非常依賴“1個標準差變化”,並不是什麼形式的變項都可見。
[額外技術細節20]
為了讓簡化分析程序,只要在jamovi模組選單裡,從”Model Coefficients”的選項中勾選”Standardized estimate”,就能計算\(\beta\),如同 Figure 10.16 的示範。
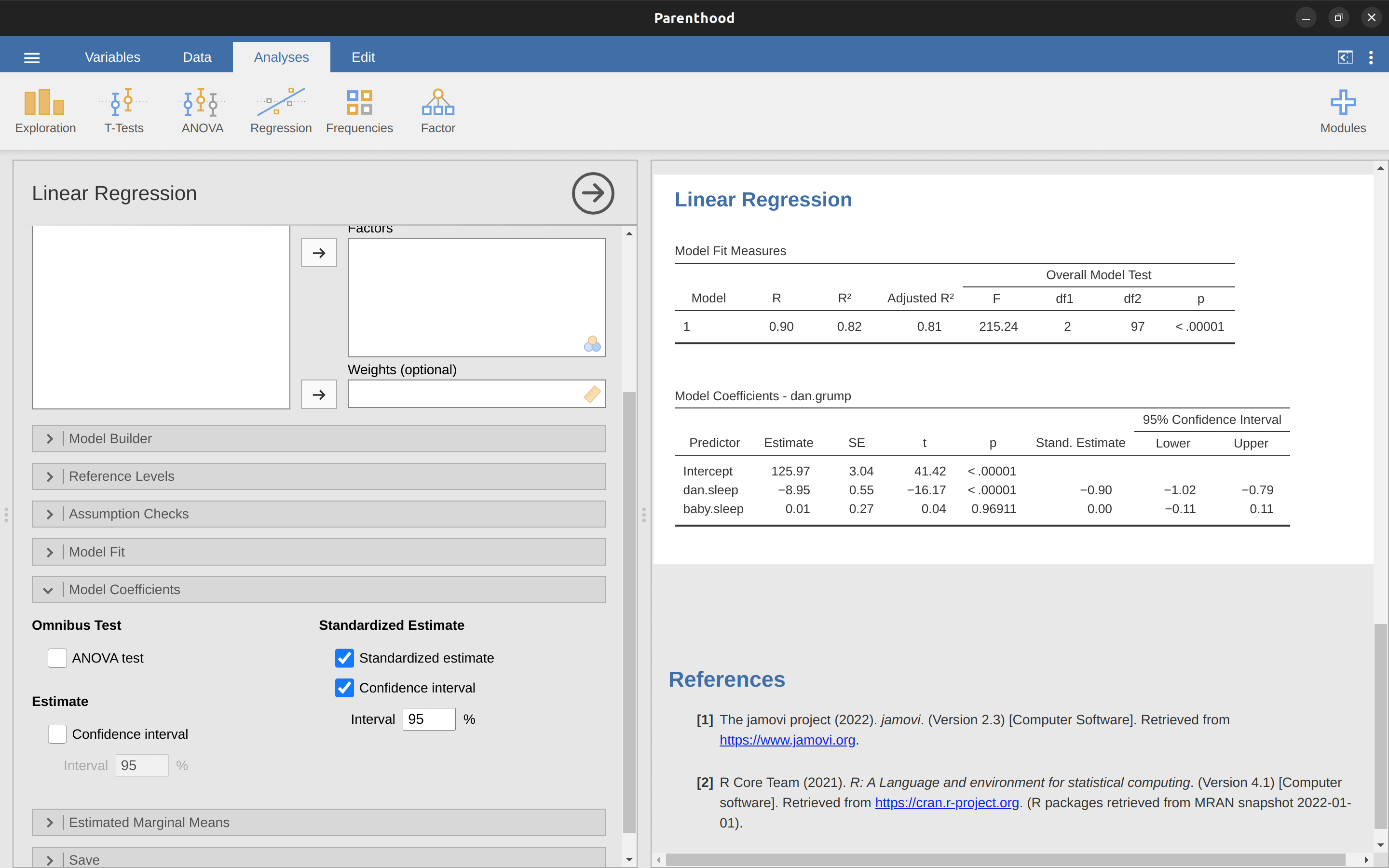
從輸出結果可明顯看出,dani.sleep是比baby.sleep有更強預測效力的變項。然而,這可能正是一個更適合使用原始係數b而不是標準化係數\(\beta\)的完美例子。畢竟,我的睡眠時間和寶寶的睡眠時間已經是同一個計量尺度。為什麼要還要將它們轉換為z分數來讓事情變得更複雜呢?
10.9 迴歸模型的適用條件
線性迴歸模型必須符合幾個適用條件(assumptions),才能解讀分析結果。在 Section 10.10 診斷迴歸模型的適用條件這個單元,我們將會學習如何檢查這些假設是否得到滿足,首先簡單說明每個假設的涵意。21
- 線性。線性迴歸模型的最基本的適用條件是\(X\)和\(Y\)之間的關係必須是線性的!無論是簡單迴歸還是多元迴歸,我們都要假設變項之間的關係是線性的。
- 獨立性:這是說變項資料的殘差彼此獨立。實際上這是條“總括一切”的適用條件,更白話地說“在殘差中找不到任何有意思的東西了”。如果還能分析出一些意料之外的資訊(例如,所有殘差都與某些未測量的變項存在明顯相關性),可能會破壞分析後的結論。
- 常態性。就像驅動許多統計方法的機率模型一樣,基本的簡單或多元線性迴歸也要符合常態性。具體來說,這條是指殘差的次數分佈逼近或符合常態分佈。實際上,即使預測變項\(X\)和依變項\(Y\)的實際資料次數分佈不符合常態分佈,只要殘差\(\epsilon\)的次數分佈符合常態的就可以了。 Section 10.10 診斷迴歸模型的適用條件有進一步說明及示範。
- 變異相等(或稱’同質性’)。嚴格來說,符合這個條件 的迴歸模型生成的所有殘差\(\epsilon_i\),都是來自一個平均值為0的常態分佈,更重要的是,每個殘差來源的機率分佈標準差\(\sigma\)都是相同的。在實務中,檢驗每個殘差都是來自同一個機率分佈是不大可能做到的事。相反地,我們真正關心的是殘差的標準差相對於所有預測值\(\hat{Y}\)是相同的,特別是多元迴歸模型的每個預測變項\(X\)所生成的預測值是相同的。
所以,要執行有效的線性迴歸分析,首先要檢查是不是符合這四個適用條件 (剛好可以縮寫成LINE)。此外,還有一些需要檢查的條件 :
沒有“不良”極端值。其實這並非必要的適用條件,但是極端值可能造成潛在的問題。就是迴歸模型雖然不會因為一兩個異常極端值,造成不符合上述任何一條適用條件(譯註~特別是線性),但是在某些情況下會引起對模型的適當性和資料可靠性的質疑。詳細說明及示範請見 Section 10.10.2 三種異常資料。
預測變項之間無相關性。執行多元迴歸模型分析時,我們不希望預測變項彼此間的存在高度相關。這並非迴歸模型的“必要”適用條件,但在統計實務是必需的。預測變項之間相關性過強(通常稱為“共線性”)可能會造成錯誤解讀分析結果。詳細說明及示範請見 Section 10.10.4 檢查共線性。
10.10 診斷迴歸模型的適用條件
譯註:這個單元全部內容都是談多元迴歸,內容文字編修排在本書最後階段進行。
本節的主要焦點是迴歸診斷,這個術語是指檢查迴歸模型假設是否得到滿足、在假設被違反時如何修正模型以及一般情況下檢查是否存在不尋常情況的技術。我將這稱為模型檢查的“藝術”,理由很充分。這並不容易,儘管有許多相當標準化的工具可以用來診斷甚至可能治愈困擾模型的問題(如果存在的話!),但在這方面真的需要運用一定程度的判斷力。在檢查這件事情或那件事情的所有細節中容易迷失,試圖記住所有不同的事物是相當耗費精力的。這會產生一個非常令人討厭的副作用,很多人在試圖學習所有工具時會感到沮喪,所以他們決定不做任何模型檢查。這有點令人擔憂!
在本節中,我描述了一些方法,用於檢查迴歸模型是否按照預期工作。它並沒有涵蓋所有您可能做的事情,但仍然比我在實踐中看到的大多數人所做的事情要詳細得多,即使在我的初級統計課程中,我通常也不會涵蓋所有這些內容。但是,我確實認為您應該了解可供您使用的工具,所以我將在這裡嘗試介紹一部分。最後,我應該指出,本節很大程度上借鑒了 Fox & Weisberg (2011) ,即與在 R 中進行迴歸分析的“car”包相關的書籍。 “car”包以提供一些出色的迴歸診斷工具而著稱,而該書本身以極為清晰的方式談論了這些工具。我不想聽起來太過於誇大,但我確實認為即使在 R 和不是 jamovi 的情況下, Fox & Weisberg (2011) 都值得一讀。
10.10.1 三種殘差
大多數迴歸診斷都圍繞著觀察殘差,到目前為止,你可能已經對統計學形成了足夠悲觀的理論,能夠猜到,正因為我們非常關心殘差,我們可能會考慮幾種不同類型的殘差。特別地,在本節中,我們將提到以下三種殘差:“普通殘差”、“標準化殘差”和“學生化殘差”。還有第四種你會在一些圖中看到的,稱為“皮爾森殘差”。然而,對於我們在本章中討論的模型,皮爾森殘差與普通殘差相同。
首先,我們關心的最簡單類型的殘差是普通殘差。這些就是我在本章前面一直提到的實際原始殘差。普通殘差僅僅是擬合值 \(\hat{Y}_i\) 和觀察值 \(Y_i\) 之間的差。我一直用符號 \(\epsilon_i\) 表示第 i 個普通殘差,並且我將繼續堅持使用它。考慮到這一點,我們有非常簡單的方程式
\[\epsilon_i=Y_i-\hat{Y_i}\]
這當然是我們之前看到的,除非我特別提到其他類型的殘差,否則我就是在談論這個。所以這裡沒有新的東西。我只是想重申一下。使用普通殘差的一個缺點是,它們總是在不同的尺度上,取決於結果變項是什麼以及迴歸模型有多好。也就是說,除非你決定在沒有截距項的情況下運行迴歸模型,否則普通殘差的均值將為 0,但每個迴歸的方差都不同。在很多情境下,特別是當你只對殘差的模式感興趣,而不是它們的實際值時,估計標準化殘差很方便,這些殘差經過規範化後標準差為 1。
[額外技術細節22]
第三種殘差是學生化殘差(也稱為 “剃刀切割殘差”),它們比標準化殘差更高級。同樣,目的是將普通殘差除以某個量,以估計殘差的某種標準化概念。23
在繼續之前,我應該指出,即使這些殘差是幾乎所有迴歸診斷的核心,你通常也不需要自己獲得這些殘差。大多數時候,提供診斷或假設檢查的各種選項將為您處理這些計算。即使如此,知道如何實際自己獲得這些東西,以防你需要進行一些非標準操作,總是很好的。
10.10.2 三種異常資料
使用線性迴歸模型時,您可能會遇到一個危險,那就是您的分析可能會對一小部分”不尋常”或”異常”的觀測值過於敏感。我之前在 Section 5.2.3 的上下文中討論過這個想法,當時是在討論用 ‘探索’ - ‘描述統計’ 下的 boxplot 選項自動識別的異常值,但這次我們需要更精確。在線性迴歸的背景下,有三個概念上不同的方式可以將觀測值稱為”異常”。這三者都很有趣,但對你的分析有很不同的影響。
第一種不尋常的觀測值是異常值。在這種情況下,異常值的定義是與迴歸模型預測的結果相差很大的觀測值。Figure 10.17 中有一個例子。在實踐中,我們通過說一個異常值是具有非常大的Studentised殘差的觀測值,\(\epsilon_i^*\),來實現這個概念。異常值很有趣:一個很大的異常值可能對應垃圾數據,例如,變項在數據集中可能被錯誤地記錄,或者可能檢測到其他缺陷。請注意,僅僅因為它是一個異常值,你不應該丟掉這個觀測值。但是,它是一個異常值,這經常是一個線索,讓你更仔細地查看該案例,並嘗試找出它為什麼如此不同。
觀測值不尋常的第二種方式是具有高槓桿作用(leverage),這發生在觀測值與所有其他觀測值非常不同的情況下。這不一定要對應大的殘差。如果觀測值在所有變項上的不尋常程度恰好相同,則實際上可能非常接近迴歸線。這方面的一個例子如@fig-fig10-18所示。觀測值的槓桿作用通常用帽子值表示,通常寫作\(h_i\)。帽子值的公式相當複雜24,但它的解釋並不複雜:\(h_i\)是衡量第i個觀測值“控制”迴歸線走向的程度。
一般來說,如果觀測值在預測變項方面遠離其他觀測值,它將具有較大的帽子值(作為粗略指南,高槓桿是指帽子值大於平均值的2-3倍;注意帽子值的總和被限制為等於\(K + 1\))。高槓桿點也值得更詳細地查看,但除非它們也是異常值,否則它們不太可能引起擔憂。
這讓我們來到了不尋常程度的第三個衡量指標,即觀測值的影響力(influence)。高影響力的觀測值是具有高槓桿的異常值。也就是說,它在某些方面與所有其他觀測值非常不同,並且距離迴歸線很遠。這在@fig-fig10-19中有所體現。注意與前兩個圖形的對比。異常值並未使迴歸線發生很大變化,高槓桿點也是如此。但既是異常值又具有高槓桿的情況,會對迴歸線產生很大影響。這就是為什麼我們稱這些點具有高影響力,而且它們是最令人擔憂的。我們用稱為Cook’s distance的衡量指標來度量影響力。25
要具有較大的Cook’s距離,觀測值必須是相當大的異常值並具有高槓桿。作為粗略指南,大於1的Cook’s距離通常被認為很大(這是我通常用作快速而簡單的規則)。
在jamovi中,可以通過單擊’Assumption Checks’ - ’Data Summary’選項下的’Cook’s Distance’複選框來計算有關Cook’s距離的信息。當你這樣做時,對於我們在本章中作為示例使用的多元迴歸模型,你將得到如@fig-fig10-20所示的結果。
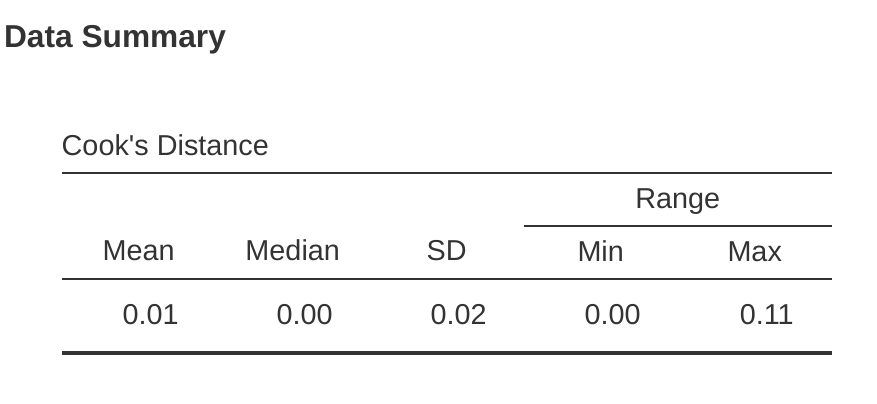
您可以看到,在這個例子中,平均Cook’s距離值為\(0.01\),範圍從\(0.00\)到\(0.11\),因此這與前面提到的指標相去甚遠,即大於1的Cook’s距離被認為很大。
接下來明顯要問的問題是,如果您確實擁有很大的Cook’s距離值,您應該怎麼辦?一如既往,沒有固定不變的規則。可能首先要做的是嘗試運行迴歸,排除具有最大Cook’s距離的異常值26,看看模型性能和迴歸係數會發生什麼變化。如果它們確實有很大不同,那就該開始深入研究您的數據集和您在運行研究時無疑在抄寫的筆記。嘗試找出該點為何如此不同。如果您開始確信這個數據點嚴重扭曲了您的結果,那麼您可能會考慮將其排除在外,但除非您對於這個特定案例與其他案例有本質上的不同並因此應該單獨處理,否則這種做法是不理想的。
10.10.3 檢測殘差常態性
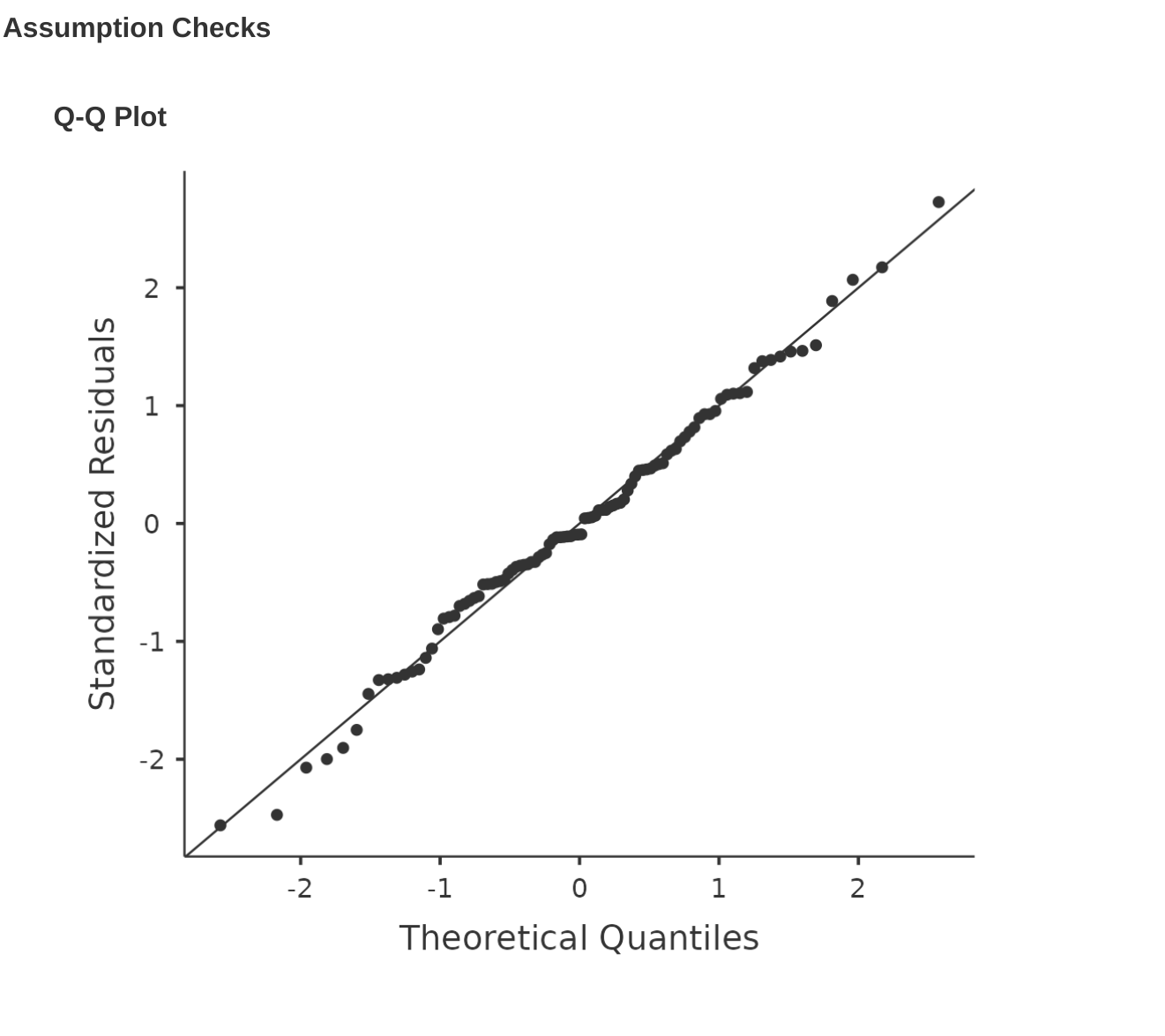
像我們在本書中討論過的許多統計工具一樣,迴歸模型依賴於常態性假設。在這種情況下,我們假設殘差呈常態分布。首先,我們可以通過 ‘Assumption Checks’ - ‘Assumption Checks’ - ‘Q-Q plot of residuals’ 選項繪製一個 QQ 圖。輸出顯示在 Figure 10.21,顯示了標準化殘差作為其根據迴歸模型的理論分位數的函數的圖。

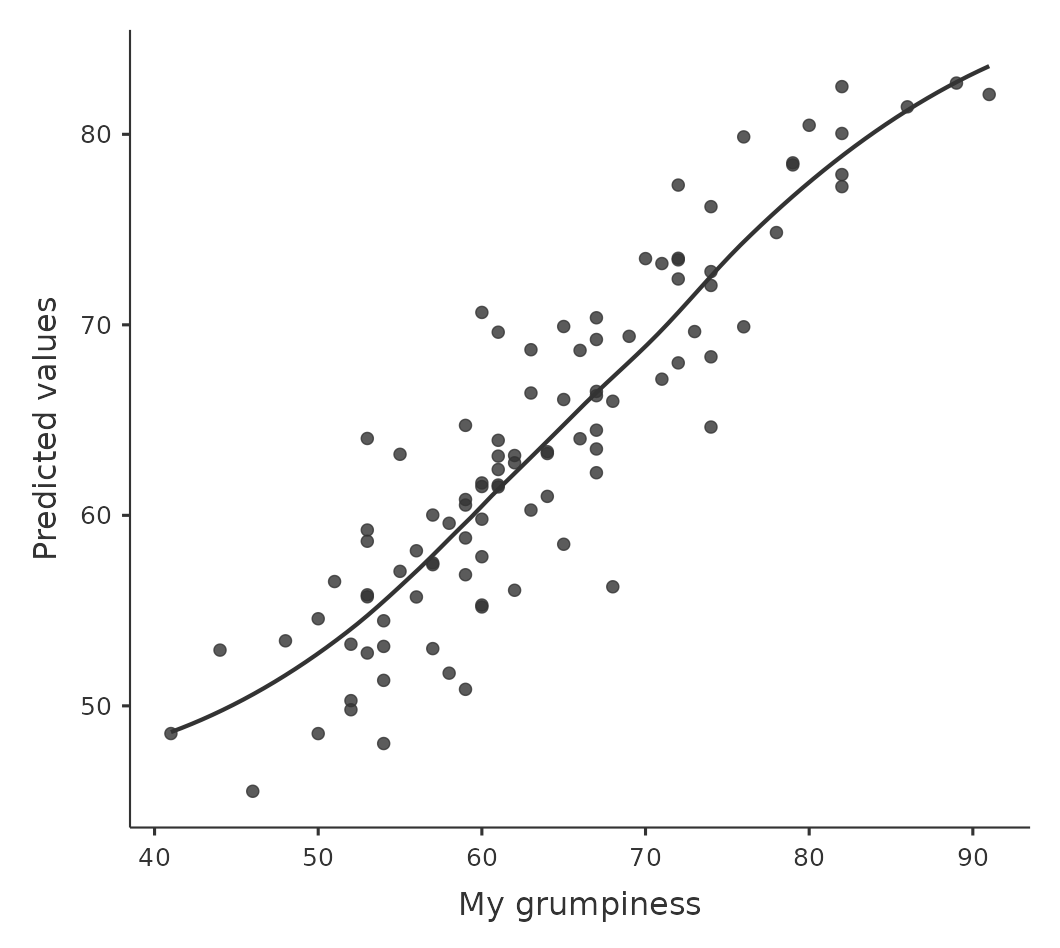
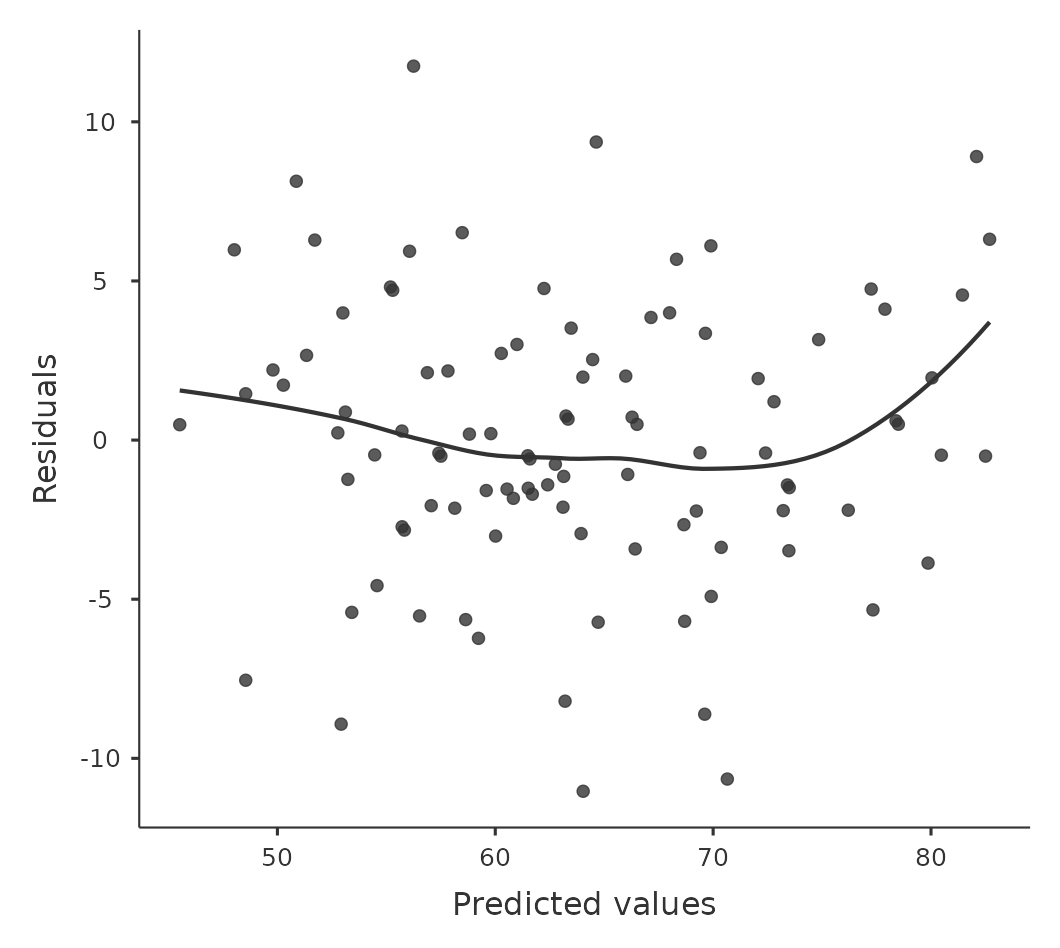
我們還應該檢查擬合值和殘差本身之間的關係。我們可以使用 ‘Residuals Plots’ 選項讓 jamovi 做到這一點,該選項為每個預測變項、結果變項以及擬合值與殘差提供了散點圖,見 Figure 10.22。在這些圖中,我們要尋找的是點的分佈相對均勻,沒有明顯的聚集或圖案。觀察這些圖,沒有什麼特別令人擔憂的,因為點在整個圖中分佈得相當均勻。在圖 (b) 中可能存在一點非均勻性,但偏差不大,可能不值得擔憎。
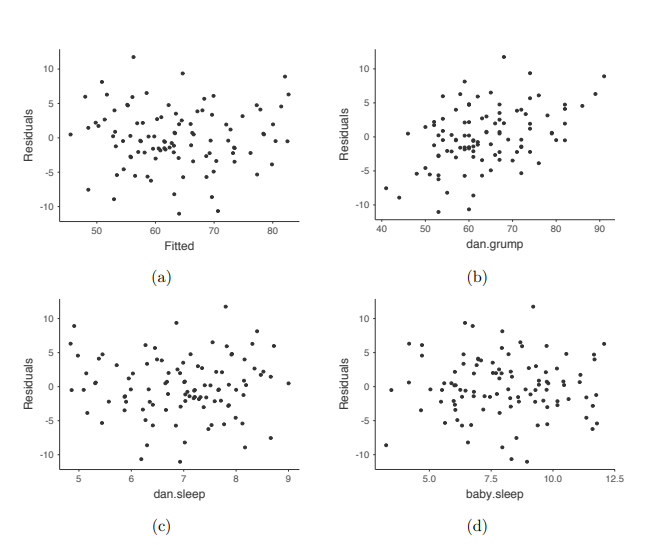
如果我們擔憂的話,那麼在很多情況下解決這個問題(以及其他許多問題)的方法是對一個或多個變項進行轉換。我們在 Section 6.3 中討論了變項轉換的基本知識,但我想特別提一下我之前沒有完全解釋的一個額外可能性:Box-Cox 轉換。Box-Cox 函數相當簡單,並且被廣泛使用。27
您可以在 jamovi 的 ‘Compute’ 變數屏幕中使用 BOXCOX 函數進行計算。
10.10.4 檢測共線性
在本章中,我將討論的最後一種迴歸診斷方法是使用方差膨脹因子(VIF),這對於確定迴歸模型中的預測變項是否彼此相關性過高很有用。模型中每個預測變項 \(X_k\) 都有一個相應的方差膨脹因子。28
VIF 的平方根具有很好的解釋性。它告訴您相應的係數 bk 的信賴區間相對於預測變項彼此完全不相關時所期望的值要寬多少。如果您只有兩個預測變項,VIF 值將始終相同,正如我們在 jamovi 的 ‘Regression’ - ‘Assumptions’ 選項中選中 ‘Collinearity’ 後可以看到的那樣。對於 dani.sleep 和 baby.sleep,VIF 均為 1.65。而由於 1.65 的平方根為 1.28,我們可以看到我們兩個預測變項之間的相關性並未造成太大問題。
為了給出我們可能會遇到具有更大共線性問題的模型的感覺,假設我要運行一個更無趣的迴歸模型,在該模型中,我試圖預測數據收集的日期,作為數據集中所有其他變項的函數。要理解這為什麼會有問題,讓我們看一下所有四個變項的相關矩陣(Figure 10.23)。
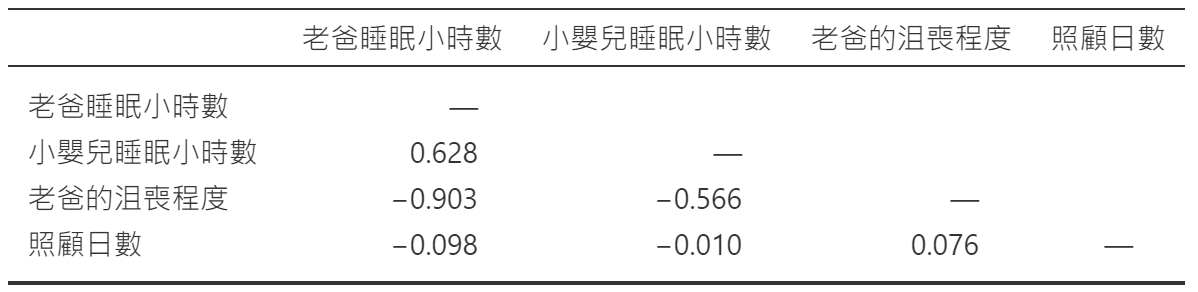
我們的預測變項之間有一些相當大的相關性!當我們運行迴歸模型並查看 VIF 值時,我們可以看到共線性對係數的不確定性造成了很大影響。首先,運行迴歸,如 Figure 10.24 所示,從 VIF 值可以看出,是的,這是一些非常好的共線性。
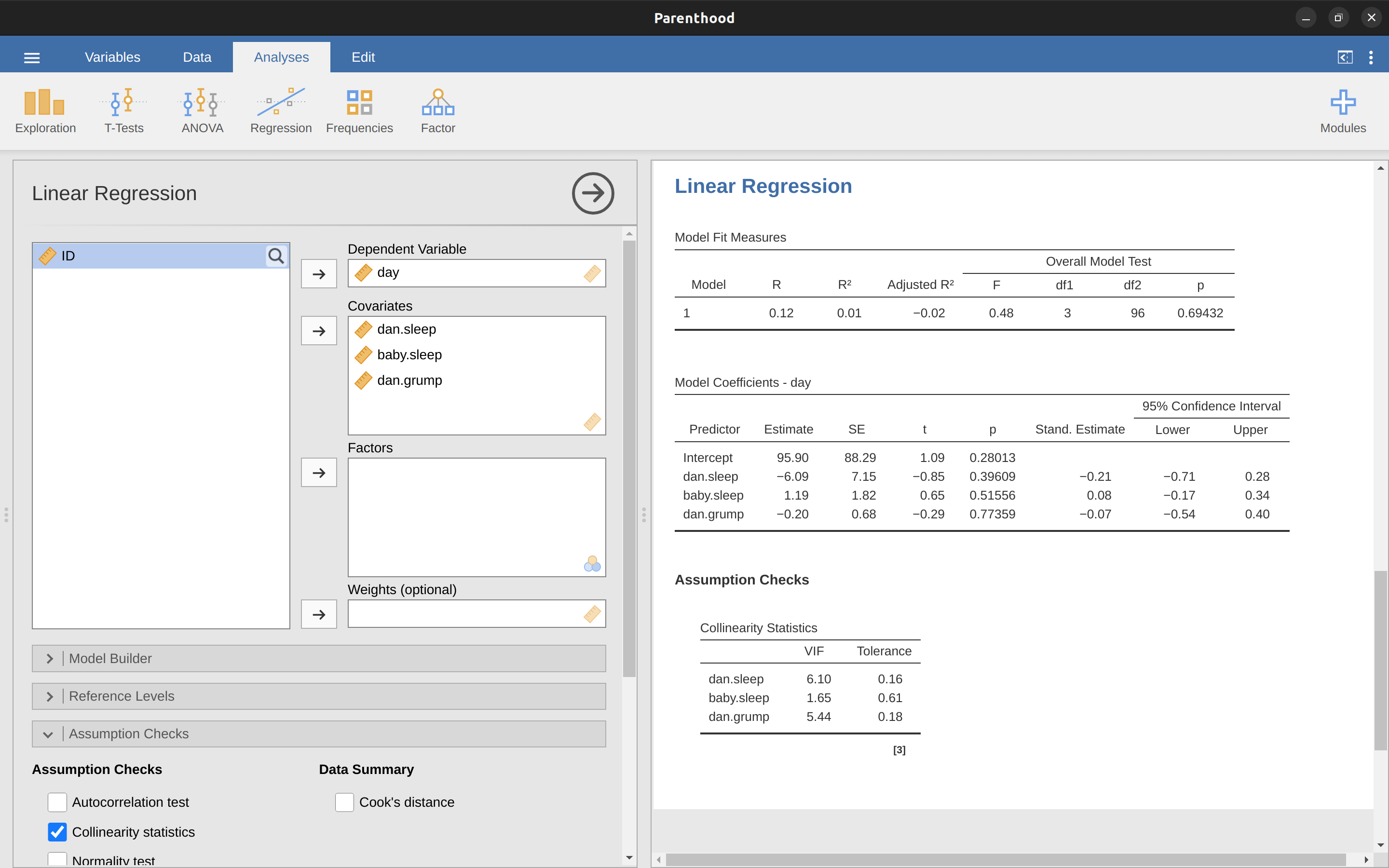
10.11 決定線性模型的變項組合
譯註:這個單元全部內容都是談多元迴歸,內容文字編修排在本書最後階段進行。
剩下的一個相當重要的問題是 “模型選擇” 的問題。也就是說,如果我們有一個包含幾個變項的資料集,哪些變項應該作為預測變項,哪些不應該包括在內?換句話說,我們有一個變項選擇的問題。通常,模型選擇是一個複雜的過程,但如果我們將問題限制在選擇應該包含在模型中的變項子集上,情況會變得簡單一些。儘管如此,我不打算試圖詳細涵蓋甚至這個範疇。相反,我將談論您需要考慮的兩個廣泛原則,然後討論一個具體的工具,jamovi 提供了這個工具,可以幫助您選擇要包含在模型中的變項子集。首先,兩個原則:
為您的選擇提供實質性的依據是很好的。也就是說,在很多情況下,您作為研究人員有充分的理由挑選一個較小的可能的回歸模型數量,這些模型在您的領域背景下具有合理的解釋。永遠不要低估這一點的重要性。統計學為科學過程服務,而不是反過來。
在您的選擇依賴統計推斷的程度上,簡單性和適合度之間存在權衡。當您向模型添加更多預測變項時,模型變得更複雜。每個預測因子都添加了一個新的自由參數(即,一個新的回歸係數),每個新參數都會增加模型對於隨機變異的吸收能力。因此,適合度(例如,\(R^2\))隨著您添加更多預測因子而持續上升,無論如何都是如此。如果您希望模型能夠很好地概括新的觀察結果,則需要避免加入過多的變項。
後者原則通常被稱為奧卡姆剃刀,並通常用以下簡潔的說法來概括:不要在必要之外繁殖實體。在這個情境下,這意味著不要僅僅為了提高你的 R2 而將一堆大致無關的預測因子扔進去。嗯,原來的說法更好。
無論如何,我們需要一個實際的數學標準,以便在選擇回歸模型時實現奧卡姆剃刀背後的定性原則。事實證明,有幾種可能性。我將談論的一個是赤池資訊量準則(Akaike information criterion)(Akaike, 1974),僅僅是因為它可以作為一個選項在 jamovi 中使用。29
AIC 值越小,模型性能越好。如果我們忽略低水平的細節,AIC 的作用就非常明顯了。左邊的項隨著模型預測變差而增加;右邊的項隨著模型複雜度的增加而增加。最佳模型是用盡量少的預測變項(低 K,右側)來擬合資料(低殘差,左側)。簡而言之,這是奧卡姆剃刀的簡單實現。
當選中 “AIC” 複選框時,AIC 可以添加到 “Model Fit Measures” 輸出表中,評估不同模型的一種笨拙方式是查看如果從回歸模型中移除一個或多個預測因子,“AIC” 值是否更低。這是 jamovi 目前實現的唯一方法,但在其他更強大的程序中,如 R,有替代方法。這些替代方法可以自動化有選擇地移除(或添加)預測變項以找到最佳 AIC 的過程。儘管這些方法在 jamovi 中尚未實現,但我將在下面簡要介紹它們,以便您了解它們。
10.11.1 逐步排除法
在逐步排除法中,您從完整的迴歸模型開始,包括所有可能的預測因子。然後,在每個「步驟」中,我們嘗試所有可能的刪除一個變項的方法,並選擇其中最好的(就最低AIC值而言)。這將成為我們的新迴歸模型,然後我們再試驗從新模型中刪除所有可能的選項,同樣選擇具有最低AIC的選項。這個過程將持續進行,直到我們得到一個具有比刪除一個預測因子的其他可能模型更低AIC值的模型。
10.11.2 逐步納入法
作為替代方法,您還可以嘗試逐步納入法。這次我們從最小可能的模型作為起點,僅考慮可能添加到模型中的選項。然而,還有一個麻煩。您還需要指定您願意接受的最大可能模型。
儘管向後和向前選擇可能導致相同的結論,但它們並不總是如此。
10.11.3 使用警告
自動變項選擇方法是具有誘惑力的東西,特別是當它們被捆綁在強大的統計程序中的(相對)簡單函數中時。它們為您的模型選擇提供了一定程度的客觀性,這很好。不幸的是,它們有時被用作掩蓋思考的藉口。您不再需要仔細考慮要添加到模型中的哪些預測因子以及它們可能包含的理論基礎。一切都通過AIC的魔力解決了。如果我們開始丟出像奧卡姆剃刀這樣的短語,那麼一切都被包裹在一個整潔的小包裹裡,沒有人可以反駁。
或者,也許不是。首先,對於什麼算作合適的模型選擇標準,幾乎沒有一致的看法。當我在本科時代被教授逐步排除法時,我們使用了F檢驗來執行它,因為那是軟件所使用的默認方法。我描述了使用AIC,並且因為這是一本入門教材,所以我只描述了這種方法,但AIC絕非統計之神的話語。它是一個近似值,在某些假設下得出的,並且只有在大樣本中滿足這些假設時才能保證起作用。改變那些假設,您就會得到不同的標準,比如BIC(在jamovi中也可用)。再換一種方法,您就會得到NML標準。決定成為貝葉斯,您將基於後驗概率比進行模型選擇。然後還有一堆我沒提到的迴歸特定工具。等等。所有這些不同的方法都有優點和缺點,有些比其他方法更容易計算(AIC可能是最容易的,這可能解釋了它的受歡迎程度)。幾乎所有方法在答案是“明顯”的情況下都會產生相同的結果,但在模型選擇問題變得困難時,存在相當多的分歧。
在實踐中,這意味著什麼?好吧,您可以花幾年時間教自己模型選擇理論,學習所有的技巧,最終決定您個人認為什麼是正確的。作為實際做過這件事的人,我不建議這樣做。您可能會在結束時更加困惑。更好的策略是表現出一點常識。如果您盯著自動向後或向前選擇過程的結果,有意義的模型接近具有最小AIC值,但被一個毫無意義的模型以微弱的優勢擊敗,那麼相信您的直覺。統計模型選擇是一個不精確的工具,正如我一開始說的,可解釋性很重要。
10.11.4 比較迴歸模型
與使用自動模型選擇程序的方法相反,研究人員可以明確地選擇兩個或多個迴歸模型以相互比較。您可以用幾種不同的方法做到這一點,具體取決於您要回答的研究問題。假設我們想知道我兒子睡眠的多少是否與我煩躁的程度有關,超出了我自己睡眠的影響。我們還希望確保測量的那一天對這種關係沒有影響。也就是說,我們對baby.sleep和dani.grump之間的關係感興趣,從這個角度看,dani.sleep和day是我們想控制的協變項。在這種情況下,我們想知道dani.grump ~ dani.sleep + day + baby.sleep(我將其稱為Model 2,或M2)是否比dani.grump ~ dani.sleep + day(我將其稱為Model 1,或M1)更適合這些數據。我們可以用兩種不同的方式來比較這兩個模型,一種基於像AIC這樣的模型選擇標準,另一種基於顯式假設檢定。我首先向您展示基於AIC的方法,因為它更簡單,並且自然地延續了上一節的討論。首先,我需要實際運行兩個迴歸,注意每個迴歸的AIC,然後選擇AIC值較小的模型,因為它被認為是這些數據的更好模型。實際上,不要立即這樣做。繼續閱讀,因為jamovi中有一種簡單的方法可以在一個表格中獲取不同模型的AIC值。30
基於假設檢定框架的某種不同方法來解決這個問題。假設您有兩個迴歸模型,其中一個(Model 1)包含另一個(Model 2)的一部分預測變項。也就是說,Model 2包含Model 1中包含的所有預測變項,再加上一個或多個其他預測變項。當這種情況發生時,我們說Model 1嵌套在Model 2中,或者可能說Model 1是Model 2的子模型。無論使用哪種術語,這意味著我們可以將Model 1視為虛無假設,將Model 2視為替代假設。事實上,我們可以用相當簡單的方式構建一個F檢驗。31
那麼,這就是我們用來比較兩個迴歸模型的假設檢定。現在,我們如何在jamovi中進行呢?答案是使用“Model Builder”選項,在“Block 1”中指定Model 1預測變項dani.sleep和day,然後將Model 2中的其他預測變項(baby.sleep)添加到“Block 2”,如@fig-fig10-25所示。這在“Model Comparisons”表格中顯示了比較Model 1和Model 2的結果,\(F(1,96) = 0.00\),\(p = 0.954\)。由於我們的p > .05,我們保留虛無假設(M1)。這種將我們所有協變數添加到零模型中,然後將感興趣的變項添加到替代模型中,然後在假設檢定框架中比較兩個模型的迴歸方法通常被稱為分層迴歸。
我們還可以使用此“Model Comparison”選項顯示一個表格,顯示每個模型的AIC和BIC,方便比較並確定哪個模型具有最低的值,如@fig-fig10-25所示。
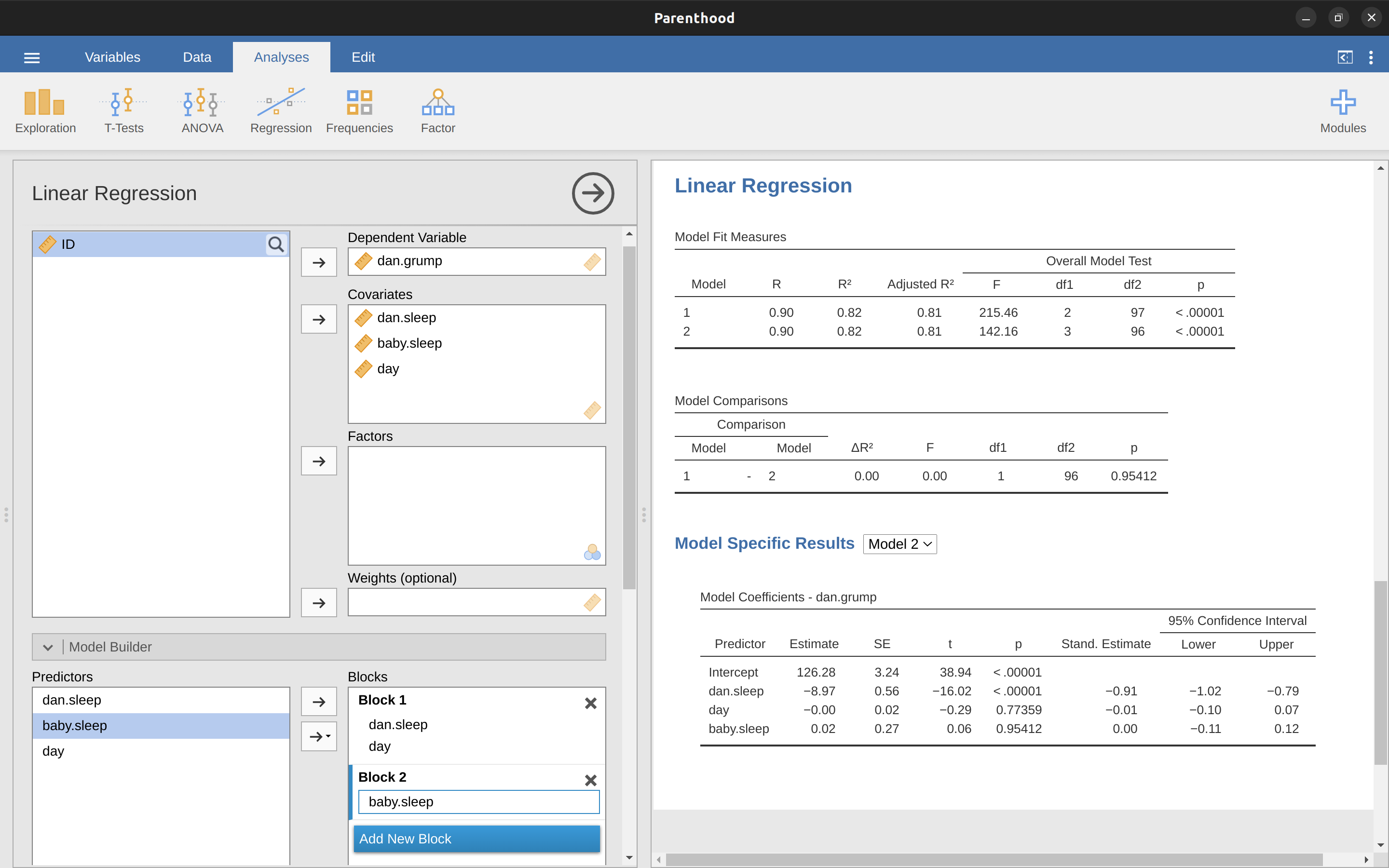
10.12 本章小結
- 想了解兩個變項之間的關聯性有多強?就計算相關係數
- 散佈圖繪製方法
- 前進下一章前必學的課題:什麼是線性迴歸模型 以及使用線性迴歸模型估計參數
- 多元線性迴歸
- 量化迴歸模型的適配性 要了解 \(R^2\) 。
- 迴歸模型的假設檢定
- 在迴歸係數的更多資訊 這一節,我們學習如何計算迴歸係數的信賴區間以及標準化迴歸係數的計算方法
- 迴歸模型的適用條件 以及診斷適用條件
- 決定線性模型的變項組合
本章在原書為第12章,繁體中文版為了整合 基礎統計方法的線性模型學習取向,改為第10章。↩︎
在2.0版之後的 jamovi 你也可以指定 “ID” 的專屬變項類型,但是對於分析資料的目的來說,指定 ID 的變項性質並不重要,因為我們不會將其包含在任何分析中。↩︎
即使是表格中的資訊對某些人來說已經足夠了,但在實務上,大多數人只需要報告一個集中量數和一個變異量數就可以了。↩︎
皮爾森相關係數的公式可以用幾種不同的方式來表示。最簡單的方式是將公式分為兩個部分。第一個部分是共變異數(covariance)(譯註:許多台灣中文教科書稱共變數)的概念。兩個變項\(X\)和\(Y\)的共變異數的數學公式是變異數公式的一般化,就是簡單描述兩個變項之間的關係,但是計算結果無法提供什麼有意義的訊息: \[Cov(X,Y)=\frac{1}{N-1}\sum_{i=1}^N(X_i-\bar{X})(Y_i-\bar{Y})\] 由於我們要將\(X\)的數值乘以\(Y\)的數值,再取乘積的平均值\(^a\),因此共變異數的公式可以視為\(X\)和\(Y\)之間的“平均外積”。共變異數的特性之一是,如果\(X\)和\(Y\)之間完全沒有關係,那麼共變異數就是零。如果變項之間是正相關(見 Figure 10.4 ),則共變異數的數值為正,如果是負相關,共變異數的數值為負。換句話說,共變異數能捕捉相關性的基本定性概念。不幸的是,共變異數的原始數值並不容易解讀,因為大小取決於\(X\)和\(Y\)所的計量單位,而且更糟糕的是,共變異數數值的單位非常奇怪。例如,如果\(X\)是dani.sleep變項(單位:小時)而\(Y\)是dani.grump變項(單位:沮喪程度),那麼共變異數的單位會是\(hours \times grumps\),我們無法解讀這是什麼意思。皮爾森相關係數則解決了這個問題,與z分數標準化原始分數的方法非常相似,將差異值除以標準差轉換為標準化分數。但是,由於共變異數來自兩個變項的數值,必須除以兩個變項的標準差才能做標準化轉換。\(^b\)換句話說,兩個變項\(X\)和\(Y\)的相關係數可以寫成這個公式:\[r_{XY}=\frac{Cov(X,Y)}{\hat{\sigma}_X\hat{\sigma}_Y}\]
—
\(^a\) 和變異數、標準差一樣,實際上我們在計算時除以的是 \(N-1\) 而不是 \(N\)。
\(^b\) 這是一個過於簡化的說法,但對於我們的目的而言已足夠。↩︎譯註~這一句原文略談測驗信效度,但是原文說法太模糊,中文翻譯做適度改寫。↩︎
譯註~原版電子書並未提供 Table 10.3 的資料,中文版配合線性模型教程,採用另一套線上教程提供的範例檔案,請見相關與線性迴歸這一節的補充。↩︎
也可以寫成 \(y = mx + c\),其中 \(m\) 是斜率,\(c\) 是截距(常數)。↩︎
\(\epsilon\) 符號是希臘字母的 epsilon。統計報告慣例使用 \(\epsilon_i\) 或 \(e_i\) 表示殘差。↩︎
原作者設想大多數讀者並不想知道普通最小平方法的細節。不過讀者若是線性代數的高手(客觀地說,很多在排名前位的大學開設統計課的教師,總是會在課堂遇到厲害的學生),會很很想知道,計算迴歸係數估計值的公式是\(\hat{b} = (X^{'}X)^{-1}X^{'}y\),其中\(\hat{b}\)是包含估計迴歸係數的數值向量,\(X\)是包含預測變項(嚴格來說,\(X\)是迴歸變項的矩陣,是實際資料數值加上一個全部都是1的數列,但這裡不討論這個區別),而\(y\)是包含依變項的數值向量。對於不是高手的讀者,這些解說並沒有太大幫助,甚至可能造成障礙。然而,由於線性迴歸有許多細節可以用線性代數的術語來表示,讀者將在本章後半部看到許多像這樣的註釋。如果讀者有能力理解其中的數學涵意,那就非常好。如果不能,可以忽略這些註釋。↩︎
一般情況下的公式:主文中我給出的方程式顯示了當您包括兩個預測變項時,多元迴歸模型是什麼樣子。毫不奇怪,如果您想要在模型中使用多於兩個預測變項,則只需添加更多的X項和更多的b係數。換句話說,如果您在模型中有K個預測變項,那麼迴歸方程就是這樣的 \[Y_i=b_0+(\sum_{k=1}^{K}b_k X_{ik})+\epsilon_i\]↩︎
“有些”指的是“非常少”(譯註:其實很多中文教科書都這樣稱呼)。在統計實務,多數人都用“R-squared”稱呼。↩︎
調整後的 \(R^2\) 值引入了一個輕微的變化到計算中,如下所示。對於具有 \(K\) 個預測變項的迴歸模型,適用於包含 \(N\) 個觀察值的數據集,調整後的 \(R^2\) 為:\[\text{adj.}R^2=1-(\frac{SS_{res}}{SS_{tot}} \times \frac{N-1}{N-K-1})\]↩︎
正式地,我們的「零模型」對應於相當簡單的「迴歸」模型,其中我們包括 0 預測變項並且僅包括截距項 \(b_0\):\(H_0:Y_0=b_0+\epsilon_i\) 如果我們的迴歸模型具有 \(K\) 預測變項,那麼「對立模型」使用多元迴歸模型的標準公式描述:\[H_1:Y_i=b_0+(\sum_{k=1}^K b_k X_{ik})+\epsilon_i\] 我們如何在這兩個假設之間進行檢驗呢?訣竅在於理解將總變異 \(SStot\) 劃分為殘差變異 SSres 和迴歸模型變異 SSmod 的可能性。我將跳過技術細節,因為我們稍後在 Chapter 12 中研究 ANOVA 時會研究這個問題。但是只需注意 \(SS_{mod}=SS_{tot}-SS_{res}\) 我們可以通過將平方和除以自由度將其轉換為平均平方。 \[MS_{mod}=\frac{SS_{mod}}{df_{mod}}\] \[MS_{res}=\frac{SS_{res}}{df_{res}}\] 那麼,我們有多少自由度呢?您可能會預料到,與模型相關的 df 與我們所包含的預測變項數量密切相關。實際上,\(df_mod = K\)。對於殘差,總自由度為 \(df_res = N - K - 1\)。現在我們已經有了平均平方值,我們可以像這樣計算 F 統計量 \[F=\frac{MS_{mod}}{MS_{res}}\] 並且與此相關的自由度為 \(K\) 和 \(N - K - 1\)。↩︎
譯註~這些適用條件在所有基礎統計方法幾乎都是必要的,這也是本書中文版將相關與線性迴歸調整為第一個學習的統計方法原因之一。↩︎
給認真的高手讀者做個補充。殘差向量是\(\epsilon=y - X\hat{b}\)。對於K個預測變項加截距,估計的殘差平方差是\(\hat{\sigma}^2 = \frac{\epsilon^{'}\epsilon}{(N - K - 1)}\)。係數估計值的共變異數矩陣是\(\hat{\sigma}^{2}(X^{'}X)^{-1}\),矩 陣的主對角線是\(se(\hat{b})\),就是標準誤估計值。↩︎
注意,儘管jamovi會自動執行多次檢定,但是沒有執行Bonferroni校正或其他類似操作(參考 Chapter 12 )。這些是預設對立假設為雙側的標準單一樣本t檢定。如果想要校正多次檢定的結果,使用者需要自行操作。↩︎
譯注~必須要勾選“Model Fit”選單裡的”F test”才能顯示自由度等資訊。↩︎
幸運的是,迴歸權重的信賴區間可以通用的方法計算出來\(CI(b)=\hat{b} \pm (t_{crit} \times SE(\hat{b}))\),其中\(se(\hat{b})\)是迴歸係數的標準誤,\(t_{crit}\)是t分佈的對應臨界值。例如,如果我們要計算的是95%的信賴區間,則臨界值是具有\(N - K -1\)自由度的t分佈中\(97.5\)的百分位數。換句話說,這與其他統計方法使用的信賴區間的計算方法相同。↩︎
嚴格來說,研究者需要將所有迴歸變項標準化。也就是說,在模型中與依變 項相關的每個“事物”都具有迴歸係數。對於到目前為止談過的迴歸模型,每個預測變項都恰好有一個迴歸變項,反之亦然。但是,統計實務中這並不是一般情況,稍後在 Chapter 13 ,我們會看到一些這方面的例子。但是,目前我們不需要太在意這種區別。(譯註~之後會提到的線性模性版範例,全都有線性迴歸模型。)↩︎
撇開這個小單元的解釋,我們可以嘗試看看實際的計算步驟。同學們可以先將所有變項資料標準化,然後再執行迴歸分析。而且其實有一種更簡單的方法可以做到這一點,預測變項\(X\)和依變項\(Y\)的\(\beta\)係數有個非常簡單的公式:\(\beta_X=b_X \times \frac{\sigma_X}{\sigma_Y}\),其中\(\sigma_X\)是預測變項的標準差,\(\sigma_Y\)是依變項Y的標準差。↩︎
譯註~這些適用條件在所有基礎統計方法幾乎都是必要的,這也是本書中文版將相關與線性迴歸調整為第一個學習的統計方法原因之一。↩︎
我們計算這些值的方法是將普通殘差除以這些殘差的(群體)標準差的估計值。由於技術原因,嘟囔囔,公式為 \[\epsilon_i^{'}=\frac{\epsilon_i}{\hat{\sigma}\sqrt{1-h_i}}\] 其中,\(\hat{\sigma}\) 在此上下文中是普通殘差的估計群體標準差,\(h_i\) 是第 i 個觀察值的“帽值”。我還沒有向你解釋帽值(但不用害怕\(^c\),它很快就會到來),所以這個公式現在可能看起來不太合理。目前,只需將標準化殘差理解為如果我們將普通殘差轉換為 z 分數。實際上,這幾乎就是事實,只不過我們的表達稍微高級一些。+++\(^c\) 或者沒有希望,也可能是這樣。↩︎
這次進行計算的公式略有不同 \(\epsilon _i^*=\frac{\epsilon_i}{\hat{\sigma}_{(-i)}\sqrt{1-h_i}}\) 注意,我們這裡的標準差估計值寫作 \(\hat{\sigma}_{(-i)}\)。這對應的是,如果你從數據集中刪除第 i 個觀察值,則將獲得的殘差標準差估計。這聽起來好像是一個很難計算的東西,因為它似乎在說你必須運行 N 個新的迴歸模型(即使是現代計算機也可能對此有些怨言,特別是如果你有一個大數據集)。幸運的是,一些非常聰明的人已經證明了這個標準差估計實際上是由以下公式給出的:\(\hat{\sigma}_{(-i)}= \hat{\sigma}\sqrt{\frac{N-K-1-{\epsilon_i^{'}}^2}{N-K-2}}\) 難道這不是一個妙計嗎?↩︎
再次,對於線性代數狂熱分子:定義帽矩陣為將觀測值向量\(y\)轉換為擬合值向量\(\hat{y}\)的矩陣\(H\),使得\(\hat{y} = Hy\)。這個名字來自這是將帽子放在y上的矩陣。第i個觀測值的帽值是這個矩陣的第i個對角元素(所以從技術上講,我應該將其寫為\(h_{ii}\)而不是\(h_i\))。哦,如果你在意,這是它的計算方法:\(H = X(X^{'}X)^{1}X^{'}\)。漂亮,不是嗎?↩︎
\(D_i=\frac{{\epsilon_i^*}^2}{K+1} \times \frac{h_i}{1-h_i}\) 請注意,這是衡量觀測值的異常程度(左邊的部分)和衡量觀測值的槓桿(右邊的部分)的乘積。↩︎
雖然目前在jamovi中進行此操作的方法不太容易,因此更強大的迴歸程序(例如R中的’car’套件)將更適合進行此更高級的分析。↩︎
對於所有的 λ 值,除了 λ = 0,有 \(f(x,\lambda)=\frac{x^{\lambda}-1}{\lambda}\)。當 λ = 0 時,我們只取自然對數(即,ln(x))。↩︎
第 k 個 VIF 的公式為:\(VIF_k=\frac{1}{1-R_{-k}^2}\),其中 \(R^2_(-k)\) 指的是如果您將 \(X_k\) 作為結果變項,並將所有其他 X 變項作為預測變項來運行迴歸,則可以得到的 R 平方值。這裡的想法是 \(R^2_(-k)\) 是 \(X_k\) 與模型中所有其他變項相關程度的非常好的衡量指標。↩︎
在線性回歸模型的上下文中(忽略與模型無關的項!),具有 K 個預測變項和截距的模型的 AIC 為 \(AIC=\frac{SS_{res}}{\hat{\sigma}^2}+2K\)↩︎
在此主題上,我應該指出,經驗證據表明,BIC比AIC更好。在我看到的大多數模擬研究中,BIC在選擇正確模型方面做得更好。↩︎
我們可以將兩個模型都應用於數據並獲得兩個模型的殘差平方和。我將它們分別表示為\(SS_{res}^{(1)}\)和\(SS_{res}^{(2)}\)。上標表示我們正在談論哪個模型。然後我們的F統計量是 \[F= \frac {\frac {SS _{res}^{(1)} - SS_{res}^{(2)}} {k}} {\frac{SS_{res}^2} {N-p-1} }\],其中\(N\)是觀察次數,\(p\)是完整模型中的預測變項數量(不包括截距),\(k\)是兩個模型之間參數的差異。這裡的自由度是\(k\)和\(N -p-1\)。值得注意的是,將這兩個SS值之間的差異表示為它自己的平方和經常更方便。也就是說 \[SS_\Delta=SS_{res}^{(1)}-SS_{res}^{(2)}\]。這樣有幫助的原因是我們可以將\(SS_\Delta\)表示為兩個模型對結果變項的預測有所不同的程度。具體來說,\[SS_\Delta=\sum_i{(\hat{y}_i^{(2)}-\hat{y}_i^{(1)})^2}\],其中\(\hat{y}_{i^{(1)}}\)是根據模型\(M_1\)對\(y_i\)的預測值,\(\hat{y}_{i^{(2)}}\)是根據模型\(M_2\)對\(y_i\)的預測值。
—
\(^d\)順便提一下,這個相同的F統計量可以用來檢驗比我在這裡提到的更廣泛的範圍的假設。非常簡要地說,注意嵌套模型M1對應於當我們將某些迴歸係數限制為零時的完整模型M2。在某些情況下,通過對迴歸係數施加其他類型的約束來構建子模型是有用的。例如,也許兩個不同的係數可能必須相加為零,或類似的情況。您可以為這些類型的約束構建假設檢定,但這有點更複雜,而且F的抽樣分布可能會是所謂的非中心F分布,這已經超出了本書的範疇!我想做的只是提醒您這種可能性。↩︎