4 歸納推理
認識各種心理學研究方法的證據強度。 從 Chandler et al. (2015) 與 Zwaan et al. (2018) 的研究報告,學習各種實驗設計搭配的統計方法,如何確認測。認識心理學研究常見的效果量指標,以及估計方法。
延伸學習:如何使用開源統計軟體規劃可重製的實驗資料分析。
4.1 證據本位的歸納推理
歸納推理的基本原則是從觀察到的具體事實或現象出發,透過整合、分析和比較所收集的證據,推論結論的可靠程度。以歸納推理得出的結論具有不確定性,因此不像 ?sec-deductive 談過的演繹推理規則,即使以邏輯原理來說前提為真,結論亦未必是確定的。雖然二十世紀中後期的科學研究大多依靠統計方法評估實驗證據,啟蒙時代開開始發展的科學方法強調運用可有效排除混淆變項的實驗設計,使研究結果能有效顯露預測是否準確。由於實驗心理學的測量方法及獨變項條件操作都有隨機性,因此學習實驗研究必須學會如何運用統計方法。
這個單元先了解各種會使用統計方法分析資料的各種研究方法,所能歸納的證據弘度,再以 Zwaan et al. (2018) 的公開資料,演練如何評估非新手經驗影響目標效果量的變化,更進一步討論所使用的效果量做為證據強度指標的有效性。
4.2 研究方法的證據強度
隨機控制試驗(Randomized Controlled Trails)是目前所有科學領域都能接受,可直接確認因果關係的研究方法。與其他已知分析資料的研究方法相比,隨機控制試驗有最高的證據等級 (level of evidence)。在有巨量研究資料發表的生物醫學研究領域,已經有跨國學術組織如GRADE (Grading of Recommendations Assessment, Development and Evaluation) 制定了證據品質分級指引,將各種醫學研究使用的研究方法,依證據可靠度將證據分為四個等級(Global Spine J., 2015):
- 高確信度:高度確信現有證據能反映真實效應,未來研究極不可能改變效應估計值。
- 中確信度:中度確信現有證據能反映真實效應,未來研究可能會改變效應估計值。
- 低確信度:低度確信現有證據能反映真實效應,未來研究極可能會改變效應估計值。
- 極低確信度:無法獲得有效證據或現有證據無法下定論。
研究方法的證據等級由強至弱排序如下:
- 系統性文獻回顧與整合分析
系統性文獻回顧整合多項主題相關,高確信度的原始研究,針對一項科學主題進行全面性的文獻搜集與批判性評價。整合分析利用統計方法綜合多個獨立研究的效應量(effect size),能提高統計效力,減少結論出錯的機會。因此,系統性文獻回顧與整合分析的證據等級排序最高(高確信度)。
- 隨機控制試驗
隨機控制試驗通過隨機分組和對照組設計,可以有效控制混淆變項的影響,保障內在效度(internal validity)達到水準。因此,隨機控制試驗的證據強度僅次於整合分析(中確信度)。
- 世代研究(cohort study)及縱貫研究(longitude study)
世代研究長期追蹤特定世代人群,能有效減少代間效應()。縱貫研究根據設定的基準條件招募個案,同時開始收集個案變化的完整資料,具有時序性證據優勢。但是兩種方法都無法有效控制混淆變項,因此證據等級較低(低確信度)。
- 橫斷研究(cross section study)
橫斷研究鎖定某一時間點取得的資料,分析變項間的關聯性,但無法推論因果關係,證據力較弱(低確信度)。
- 個案報告與個案系列報告
個案報告記錄特定個人的特質與經驗。個案系列報告收集一系列相似的個人記錄。雖然能提供初步知識,但是證據品質較低(極低確信度)。
- 專家意見
雖有其價值,但屬於最低等級的證據(極低確信度)。
透過上述評比,可以看出研究方法的證據等級,與研究設計的嚴謹程度,以及排除研究結果出錯的可能性極有關係。進一步地說,我們看到任何最新發表的研究結果,都要預期可能被未來發表的研究更新。所以根據這一套等級指引,我們可以評估以上研究方法產生的結果,被其他研究者指出錯誤,而需要更新或廢棄的風險程度:
- 低出錯風險:研究遵循優質設計、執行及避免出錯的原則。
- 低出錯風險:研究可能存在某些錯誤,但不太可能使結果失效或引入顯著偏差。
- 高出錯風險:研究設計與執行存在顯著缺陷,可能增加出錯風險並使結果失效。
- 高出錯風險:研究可能存在顯著錯誤。例如缺乏比較組別,無法直接評估重要指標。
證據等級越高的研究設計,表示研究者要遵守的條件限制,以及要控制的條件越繁複細緻。如果一項研究的設計能達到應具備的條件,產生的研究結果出錯風險會有該類設計能達到的最高控制水準。然而,如果一項研究設計應遵守或控制的條件不夠完備,出錯風險就會增加。並非自我宣稱所執行的研究是隨機控制試驗,或者等級更高的整合分析,就能保證研究結果能達到最低出錯風險。這也是當代研究者需要了解開放科學實踐方法,以及可重製研究操作的主要理由。
4.3 實驗資料結構與測量誤差
在此以 Zwaan et al. (2018) 的實驗設計為示範,探討實驗資料裡因隨機性產生的測量誤差,如何以統計分析方法解析。對於各項重製實驗,都有三個獨變項: Wave(Within Participant) X Similarity(Between Participant) X Specific Condition(Within Participant)。除了各項實驗的關鍵參與者內獨變項(Specific Condition),每項實驗都有測試非新手經驗的參與者內參與梯次(Wave),以及可能影響非新手經驗的刺激性質異同性(Similarity), Zwaan et al. (2018) 以參與者間隨機分組操作。
4.3.1 定義依變項算術元素
不論實驗依變項是反應時間或反應正確率,每項實驗的測量分數(Y)來源都能依獨變項條件解析其中的隨機成份。首先定義各獨變項條件的算術元素:
刺激相同的參與者~ \(P_{s1}, P_{s2}, ... P_{sn}\)
刺激不同的參與者~ \(P_{d1}, P_{d2}, ... P_{dn}\)
Wave ~ \(w_1, w_2\)
Similarity ~ \(S_s, S_d\)
Condition ~ \(C_1, C_2\)
各分組依變項平均分數的算術元素表列如下:
| 參與者分組 | 參與者代碼 | 獨變項因子組合 | 依變項平均分數 |
|---|---|---|---|
| \(P_{s1}\) | \(w_1S_sC_1\) | \(Y_{11s1}\) | |
| \(P_{s2}\) | \(w_1S_sC_1\) | \(Y_{21s1}\) | |
| Same | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | |
| \(P_{sn}\) | \(w_1S_sC_1\) | \(Y_{n1s1}\) | |
| \(\overline{Y}_{.1s1}\) | |||
| \(P_{s1}\) | \(w_1S_sC_2\) | \(Y_{11s2}\) | |
| \(P_{s2}\) | \(w_1S_sC_2\) | \(Y_{21s2}\) | |
| Same | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | |
| \(P_{sn}\) | \(w_1S_sC_2\) | \(Y_{n1s2}\) | |
| \(\overline{Y}_{.1s2}\) | |||
| \(P_{s1}\) | \(w_2S_sC_1\) | \(Y_{12s1}\) | |
| \(P_{s2}\) | \(w_2S_sC_1\) | \(Y_{22s1}\) | |
| Same | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | |
| \(P_{sn}\) | \(w_2S_sC_1\) | \(Y_{n2s1}\) | |
| \(\overline{Y}_{.2s1}\) | |||
| \(P_{s1}\) | \(w_2S_sC_2\) | \(Y_{12s2}\) | |
| \(P_{s2}\) | \(w_2S_sC_2\) | \(Y_{22s2}\) | |
| Same | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | |
| \(P_{sn}\) | \(w_2S_sC_2\) | \(Y_{n2s2}\) | |
| \(\overline{Y}_{.2s2}\) | |||
| \(P_{s1}\) | \(w_1S_dC_1\) | \(Y_{11s1}\) | |
| \(P_{s2}\) | \(w_1S_dC_1\) | \(Y_{21s1}\) | |
| Different | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | |
| \(P_{sn}\) | \(w_1S_dC_1\) | \(Y_{n1s1}\) | |
| \(\overline{Y}_{.1d1}\) | |||
| \(P_{s1}\) | \(w_1S_dC_2\) | \(Y_{11s2}\) | |
| \(P_{s2}\) | \(w_1S_dC_2\) | \(Y_{21s2}\) | |
| Different | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | |
| \(P_{sn}\) | \(w_1S_dC_2\) | \(Y_{n1s2}\) | |
| \(\overline{Y}_{.1d2}\) | |||
| \(P_{s1}\) | \(w_2S_dC_1\) | \(Y_{12s1}\) | |
| \(P_{s2}\) | \(w_2S_dC_1\) | \(Y_{22s1}\) | |
| Different | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | |
| \(P_{sn}\) | \(w_2S_dC_1\) | \(Y_{n2s1}\) | |
| \(\overline{Y}_{.2d1}\) | |||
| \(P_{s1}\) | \(w_2S_dC_2\) | \(Y_{12s2}\) | |
| \(P_{s2}\) | \(w_2S_dC_2\) | \(Y_{22s2}\) | |
| Different | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | |
| \(P_{sn}\) | \(w_2S_dC_2\) | \(Y_{n2s2}\) | |
| \(\overline{Y}_{.2d2}\) |
4.4 運用統計方法歸納實驗結果
這一節的內容建議搭配統計軟體學習,可以參考用jamovi上手統計學了解對應的原理及操作方法。
4.4.1 實驗設計與統計分析模型
如果Wave與Similarity不影響specific condition的平均值差異,一項重製實驗的每次試驗原始分數,即符合線性模型(1):
\[Y_{ijkl} \sim \overline{Y}_{...} + \alpha_j + \beta_k + \gamma_l + \varepsilon_{i(k)} \dots (1)\] i = 1,2,3, …, 160
\(\alpha\) ~ Wave, j = 1, 2
\(\beta\) ~ Similarity, k = s, d
\(\gamma\) ~ specific condition, l = 1, 2
\(\varepsilon\) ~ residuals 下標符號提示參與者間獨變項
如果Wave與Similarity並無差異,則符合線性模型(1):
\[Y_{il} \sim \overline{Y_{.}} + \gamma_{l} + \varepsilon_i \dots (2)\]
i = 1,2,3, …, 160
\(\gamma\) ~ specific condition, l = 1, 2, 3, …, 8
模型(1)適用多因子變異數分析,模型(2)適用單因子變異數分析或t檢定。
- 如何透過線性模型選擇jamovi分析模組?
- 如何透過線性模型了解jamovi分析模組的選項設定?
4.4.2 效果量的估計與運用
Cohen’s d計算器 by James Uanhoro
jamovi的t檢定模組
重製附錄內統計表的Cohen’s d (1) 從各條件平均值 (2) 從每位參與者的平均分數
提示題: 如何選擇估計效果量的公式及計算器?
提示題: 如果文獻報告沒有提供效果量,要怎麼估計?
解讀 Zwaan et al. (2018) 的Figure 1(下圖取自論文網頁)。
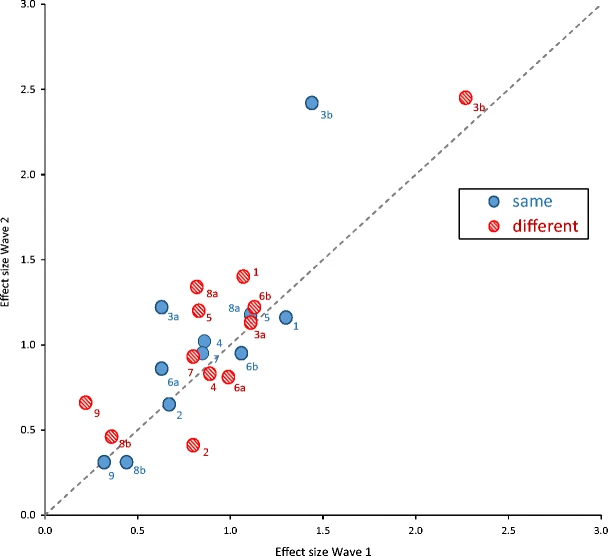
運用以上介紹,嘗試重製附錄中每項實驗的統計資訊,以及Table S1 ~ Table S10的效果量數值。
4.4.3 直接再現重製研究的評估
在台灣地區再重製九項認知實驗,要考慮那些條件?
- 在地或國外參與者
- 實驗環境是實體空間或網路
- 實驗軟體及平台的選擇
- 因軟體及平台的設定,實驗程序需要的設定
- 因參與者的背景,實驗材料要做的調整
我們設想讀者或參與課程的學生都已經學過基礎統計,應該知道現代實驗科學大量依賴p值(p value)判斷隨機控制試驗的實驗結果,有沒有出現設計實驗時的預期效果。生物醫學領域有學者主張如果採用上述各種方法的研究,最後是以p值判斷研究結論,應該設定對應證據強度的建議判斷指標(Gibson, 2021; Pocock et al., 2015)。有些心理科學領域的開放科學提倡者,主張除了次數主義統計學(Frequentist statistics),心理學家也應該學習使用貝氏統計(Bayesian statistics)(Colling & Szűcs, 2021)。他們的理由是次數主義統計學只強調控制干擾實驗結果的誤差,並未直接估計應測出的實驗效果。貝氏統計提供量化方法,研究者能用貝氏統計指標量測支持假設的證據強度,更適合要得到確證性結論的心理學研究。本書之後的單元將再深入討論兩種統計思維,我們先來討論科學心理學的知識更新進程。