第5單元 單一樣本的推論統計
這個單元介紹第一種推論統計方法:單一樣本檢定。這類方法雖然少見於心理科學研究,但是使用上要注意的基本條件相對較少,是許多統計教材的推論統計入門單元。
透過第1單元登場的Emily Rosa專題研究,我們以這個例子學習假設檢定的基本觀念,並運用二項檢定及單一樣本t檢定分析Emily Rosa的資料。學習t檢定分析的運程,我們將認識另一種連續型隨機變數:t分數,以及其機率函數:t分佈。還有學習信賴區間的觀念與使用方法。
5.1 預先註冊
解說如何使用統計方法之前,請讀者先認識預先註冊(preregistration)(Lindsay, Simons, and Lilienfeld 2016)。預先註冊是一種將科學思考轉化為可徵信報告的流程,就統計實務來說,只有兩個步驟。步驟一:執行分析之前先留下計畫,說明用什麼統計方法分析手上的資料,判斷分析結果的標準是什麼;步驟二:按照計畫程序分析資料,呈現按計畫程序得到的分析結果。
使用任何新的統計方法時,可以透過預先註冊檢視自己有沒有學到正確的使用方法。要留下分析計畫,你必須掌握使用這種統計方法分析手上資料的合理性,以及了解各種分析結果的意義。做法看似很簡單,但是經驗越豐富的研究者,在養成過程中如果沒有建立清楚的觀念,遇到不如預期的資料,經常會陷入天人交戰的局面。只要是按步就班收集資料,無論分析結果是否符合預期,呈現出來都有助科學知識的更新。雖然預先註冊還沒有完全被全世界心理科學家接受,甚至正確認識,正在開始學習統計的你,了解預先註冊的觀念,可以培養判斷分析結論的。
5.2 虛無假設顯著性檢定
我們在單元4.6得知次數主義的要旨,是根據得到某種分析結果的假設為前提(\(\theta\)),評估觀察得到當下資料(D)的條件機率(\(P(\frac{D}{\theta})\))。這個條件機率能以對應的機率函數計算與模擬,關鍵在於許多問題一開始無法明確預測會得到什麼結果,只能確定最不可能被現在的觀察資料證實的假設,得到當前結果的條件機率(\(P(\frac{D}{\theta})\))必定不會超過研究者能接受的水準。這種假設被稱為虛無假設(Null Hypothesis,許多統計教材簡記為\(H_0\)),以虛無假設的機率分佈計算得到當前結果的條件機率,就是p值。這是虛無假設顯著性檢定的基本思考方式,也是本書介紹的所有統計方法的運作流程。
5.2.1 虛無假設與對立假設
我們在單元3.1.2討論投擲一枚正反面出現機率相等的硬幣,做一系列試驗得到的所有結果之可能機率,可用適當的機率函數計算。這個試驗案例改編自第一個本寫進教科書的假設檢定案例(Fisher 1966),教科書的作者Ronald Fisher是假設檢定方法的奠基者之一。在Fisher的著作中,他提到曾在一次英式下午茶場合,遇到一位女士宣稱有能力分辨喝下的奶茶是先倒茶再加牛奶,還是先倒牛奶再加茶。當場他設計一個實驗,安排四杯奶茶先倒茶再加牛奶,以及四杯奶茶先倒牛奶再加茶,配成四組請這位女士一一試喝,每一組會先喝到那一種由調製者隨機決定。這個設計如同有四枚硬幣,先不讓對方看投擲的結果,請對方猜正面與反面朝上各有多少枚。
Fisher如此設計的想法,是因為在場沒有人真的知道那位女士的分辨能力。如果這位女士不是靠任意猜測的,我們可以假設她正確分辨一對奶茶調製方法的機率是\(\theta_1\),根據二項分佈機率函數,她正確分辨所有奶茶如何調製的比率就是\(P(\theta_1)\)。但是既然沒有人知道她的真本事,就算測試結果是百分之百,也無法說服眾人\(\theta_1\)不是50%。當時的Fisher設定另一種假設:如果這位女士是靠猜測的,每一組分辨成功的機率是50%,簡記為\(\theta_0\)。運用單元3.3.1學習到二項分佈計算方法,可以算出要正確猜對至少三對的機率是0.24,全部猜對的機率則是0.01。也就是說,這位女士全靠猜測的話,四組奶茶的測試全部正確的機率不到5%。
Fisher的奶茶試驗所設定的\(\theta_0\),就是現代進行推論統計分析之前,要設定的虛無假設\(H_0\);茶會當下想測試但是沒人知道的分辨能力就是對立假設(alternative hypothesis, \(H_1\))。對於試驗結果的判斷,Fisher的判斷原則來自計算的機率函數,而現代推論統計的判斷原則來自模擬的機率函數。後者是與Roland Fisher同時代的兩位統計學者,Jerzy Neyman與Egon Pearson的貢獻,也是現代推論統計方法需要根據p值判斷分析結果的原因。
要了解如果運用模擬的機率函數進行虛無假設統計檢定,我們設定Fisher的奶茶試驗擴張到20組奶茶,如果這位女士每次測試的答對率有95%,就能模擬虛無假設與對立假設的機率分佈,也就是一次答對率各為0.5與0.95,試驗次數都是20次的二項機率分佈。
以答對率0.95的二項機率分佈製造這位女士可能的答對次數,放到答對率0.5的二項機率分佈,就能算出如果她是靠猜測的,發現這項結果的條件機率,也就是p值。我們知道次數主義的宗旨是長期實驗結果的累積,模擬10000次結果,就能製造10000筆p值。
| p_values | Freq |
|---|---|
| 0 | 7364 |
| 2e-04 | 1895 |
| 8e-04 | 588 |
| 0.0051 | 126 |
| 0.0208 | 19 |
| 0.0612 | 7 |
| 0.1372 | 1 |
由表5.1可知,10000次實驗裡,大於.05的結果有8筆,大於.01的結果總計27筆。許多運用虛無假設顯著性檢定的分析,採用.05或.01為檢定水準的理由來自類似的模擬程序。研究者要採用那一種檢定水準,最佳的策略是了解要測試的虛無假設與對立假設性質。理解計算的與模擬的機率分佈,我們可以歸納兩者性質如下:
- 虛無假設(\(H_0\)):發現當下實驗結果的機率相對較低的實驗結果抽樣分佈。
- 對立假設(\(H_1\)):發現當下實驗結果的機率相對較高的實驗結果抽樣分佈。
運用隨機程序製造符合虛無假設與對立假設的實驗結果抽樣分佈,我們能從圖5.1看到兩者差異。
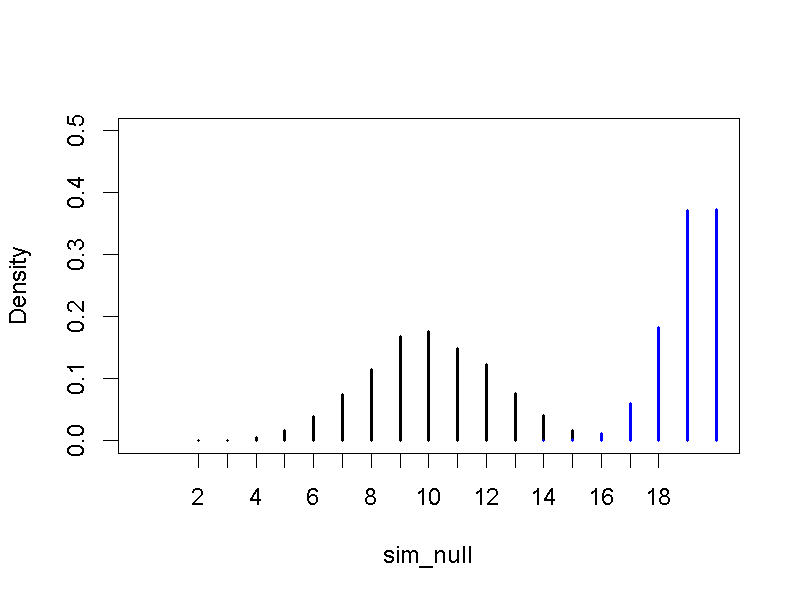
圖 5.1: 下午茶實驗測試20組的虛無假設(黑色線條)與對立假設(藍色線條)模擬抽樣分佈
5.2.2 型一與型二錯誤率
為了判斷當下的實驗結果是不是屬於虛無假設的抽樣分佈,必定發生兩種判斷失誤:(1)錯誤肯定(False Positive)~判定資料不支持虛無假設,實際上結論錯誤。(2)錯誤否定(False Negative)~判定資料支持虛無假設,實際上結論錯誤。運用虛無假設與對立假設的模擬正確率數值,總計大於正確率0.95的虛無假設數值個數,以及小於正確率0.95的對立假設數值個數,就是10000次實驗的結論為錯誤肯定與錯誤否定的失誤次數。換算為百分比,就是一般所稱的型一錯誤率與型二錯誤率。以一次測試20組奶茶的例子來說,我們設定答對18組是檢定水準,運用示範檔案的模擬程序,就可以得到如表5.2的型一錯誤率(H0 is true, Reject H0)與型二錯誤率(H0 is false, Accept H0)。
| H0 is true | H0 is false | |
|---|---|---|
| Reject Ho | 0.06 | 0.63 |
| Accept H0 | 0.94 | 0.37 |
介紹到此,讀者應該發現本書與其他統計教材的不同之處。我們先認識什麼是p值,接著才討論什麼是型一(\(\alpha\))與型二(\(\beta\))錯誤率,而且特意淡化檢定水準的說明。這是為了讓讀者,特別是實務經驗還不豐富的新手了解,p值與型一錯誤率是兩回事。即使以上例子的型一錯誤率剛好等於.05,與常見的檢定水準相同,但是檢定水準其實是由研究者自己設定,型一錯誤率是估計根據真實結果與檢定水準的比較,否定虛無假設卻結論錯誤的最大機率。仔細檢視示範檔案的模擬程式碼,就能知道計算p值與估計犯錯機率的機制,是完全不同的。
相對於型一錯誤率,型二錯誤率指根據檢定水準判斷實際得到的p值,否定對立假設卻不正確的最大機率。能經得起長期考驗的研究結果,型一與型二錯誤率應該越小越好。設定檢定水準體現研究者對型一錯誤率的期許,型二錯誤率與研究者肯定對立假設的正確率互為補集,在統計學裡後者被稱為考驗力(Power),也就是表5.2的0.63。除了透過儘可能最小的檢定水準得到顯著結果,經得起考驗的研究結果也要有儘可能最大的考驗力。我們在第6單元,將進一步認識什麼是考驗力,以及如何確保研究結果有起碼的考驗力。
5.2.3 母數與無母數檢定
單元4.5提過有母數與無母數的機率分佈的區別,兩者關鍵差異是母群體的機率函數參數有沒有平均數與標準差/變異數。平均數在機率論又名期望值(Expected value),因為展現隨機試驗所有結果的函數,代表每種結果的隨機變數(x),與各自發生機率(p)的乘積總和,也就是平均數。機率論裡簡記為\(E(x)\),其中的x正是隨機變數。例如Roland Fisher版本的奶茶試驗,受測者純粹靠猜測的期望值是\(0\times\frac{1}{70} + 1\times\frac{16}{70}+2\times\frac{36}{70} + 3\times\frac{16}{70}+4\times\frac{1}{70} = 2\)。也就是受測者靠著純粹猜測,最可能得到的試驗結果。
在第2單元學習統計量數時,己知平均數是集中量數,與之相關的變異量數是變異數與標準差。既然標準差是變異數的開根號,我們只要了解變異數是每個隨機變數與期望值之差異平方的期望值,如以下公式:
\[Var(x) = E[(x - E(x))^2]\]
這個公式可以展開為兩種期望值:第一種是隨機變數平方的期望值\(E(x^2)\),第二種是隨機變數期望值的平方\(E(x)^2\),所以這個公式可以寫成:
\[Var(x) = E(x^2) - E(x)^2\]
我們在單元4.3知道所有統計方法的操作都是根據樣本的機率函數,或者說抽樣分佈。由於平均數與變異數都是母群體機率函數的參數,樣本的機率函數的參數也有這兩者。因此實際資料的平均數與變異數可以視為抽樣分佈的參數估計值,而且有的統計方法就算不清楚母群體的參數是多少,也能使用樣本的平均數與變異數替代。
除了上述的參數估計,母數統計與無母數統計還有一些不同之處,在之後的單元再做介紹。如果兩種方法都可以分析手上的資料,何者較好並沒有絕對的標準,只有何者最適何分析面前的問題。以下用Emily Rosa的專題研究資料,示範無母數統計–二項檢定與母數統計–單一平均數t檢定的分析程序。
5.3 單一比率二項檢定
Emily Rosa在論文中提到,當年先從學校作業發想,找了15位自願參與的治療師進行第一次實驗。之後有記者注意,為了進行採訪,找了包括曾參與第一次實驗部分人士與其他治療師等13位自願者,進行了第二次實驗(Rosa et al. 1998)。因此,本單元以第一次實驗結果示範單一比率二項檢定。
二項檢定只要資料是0到1之內的比率值,配合資料的樣本數就能進行顯著性檢定,判斷資料能不能否定虛無假設。所以Roland Fisher的奶茶測試,可以用這種方法分析。設計與假設和奶茶測試如出一轍的TT測試,當然可以分析結果。
Emily Rosa假設如果治療師真的有本事,答對率應該明顯高於50%,或者十次試驗有超過五次答對。符合假設的母群體機率函數的隨機變數只有兩個數值:1(正確)與0(錯誤)。兩個數值代表的事件機率分別為0.5,因此母群體機率函數的圖示如同圖5.2。
圖 5.2: 單一比率二項檢定之母群體機率函數
Emily Rosa第一次實驗收集了15人共150次回答正確或錯誤的紀錄,使用這個原則進行一萬次模擬,就能得到圖5.3的樣本機率函數。
圖 5.3: 單一比率二項檢定之樣本機率函數
5.3.1 中央極限定理
這個例子體現母群體的機率函數,不必然等於樣本機率函數。只要產生樣本的隨機方法符合母群體機率函數,樣本機率函數就會接近常態分佈。這種現象在機率論稱為中央極限定理,最早由十八世紀的法國數學家亞伯拉罕·棣美弗與十九世紀的皮耶-西蒙·拉普拉斯證明。中央極限定理是今日我們能運用樣本極率函數,或者抽樣分佈,以手中資料進行推論統計的基礎。
我們不必深入了解如何推導中央極限定理,只是必須知道如何判斷模擬的抽樣分佈確實是常態分佈。最直接的方法是判讀分位圖(Q-Q plot):圖5.4是構成圖5.3的隨機數值,所繪製的分位圖。分位圖的橫軸(Theoretical Quantilies)是隨機數值的標準化分數,也就是z值;縱軸(Sample Quantiles)是隨機數值裡,對應每個z值的累積百分比的分位數。分位圖包括兩種數值的散佈圖,以及通過兩類數值皆為0的迴歸直線。符合中央極限定理的抽樣分佈,繪製出的散佈圖資料點,必定完全貼合迴歸直線。統計語言R有內建分位圖繪圖函式。讀者可自行檢視jamovi模擬程序示範檔案,Rj套件操作視窗裡的qqplot與qqnorm函式。
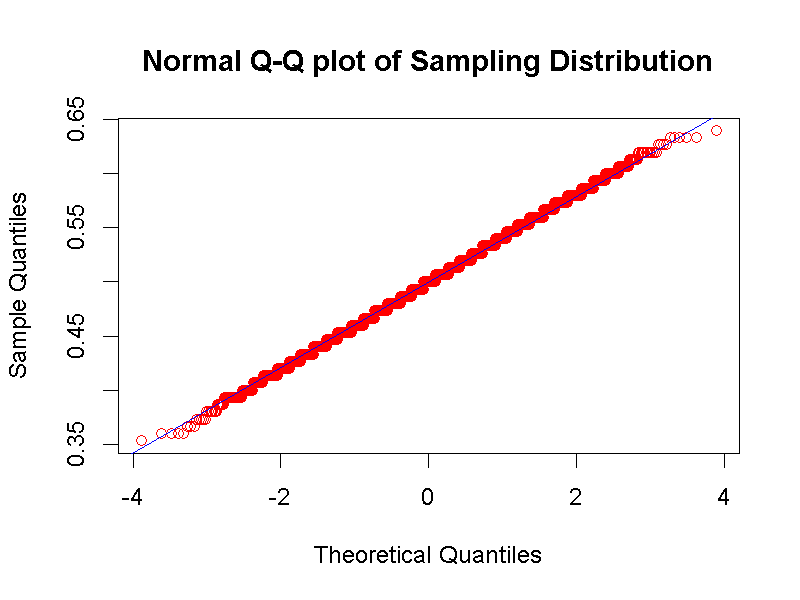
圖 5.4: 單一比率二項檢定之樣本機率函數分位圖
由此例開始,本書介紹的推論統計方法,只要所根據的抽樣分佈符合常態分佈,都會使用分位圖檢驗抽樣分佈。我們在第6單元,進一步會學到即使完全不知母群體機率函數的模樣,但是只要肯定存在母數(期望值),樣本機率函數是接近當下樣本平均數與變異數的常態分佈。
5.3.2 檢定程序示範
此處以JASP示範如何使用二項檢定分析Emily Rosa的第一次實驗資料。JASP的Data Library有收錄這筆資料,讀者除了可自行開啟,也可下載本書的JASP示範檔案,觀摩如何使用Frequencies -> Binomial Test模組設定操作。
因為Emily Rosa假設有本事的治療師,正確率應該明顯高於50%,因此設定虛無假設:proportion = 0.5,對立假設:proportion > 0.5。所以設定視窗裡的Test value是0.5,Hypothesis勾選> Test value。
JASP示範檔案之中的顯著性檢定結果回報兩個p值,各自代表正確與錯誤的回答比率都不能否定虛無假設。這些p值的計算是根據假設每次答對率為0.5,累積150次嘗試的二項分佈。再以實際的正確次數或錯誤次數,計算該次數到總次數的相對累積機率,這項p值即代表這群治療師的答對率有沒有高於0.5,如圖5.5是正確次數的二項檢定p值;而圖5.6是錯誤次數的二項檢定p值。讀者可在jamovi模擬程序示範檔案,探索以相同規模重做一次Emily Rosa的實驗,所有治療師要做對多少次,單一比率二項檢定才能肯定他們真有本事?
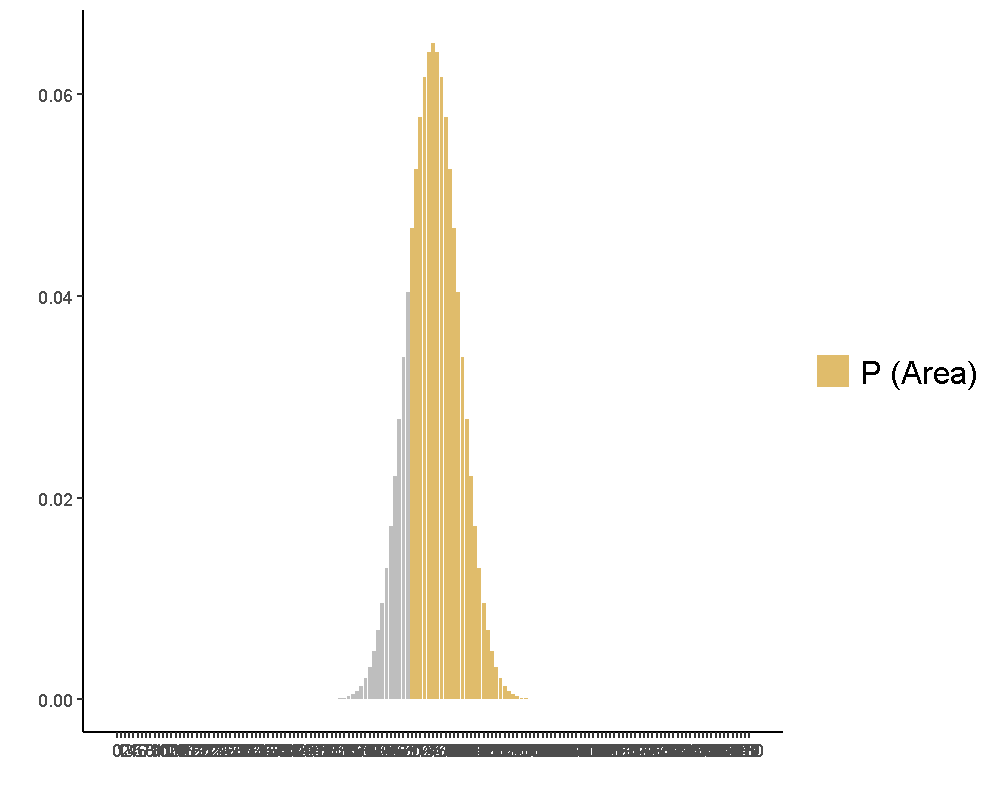
圖 5.5: 單一比率二項檢定之正確次數p值視覺化
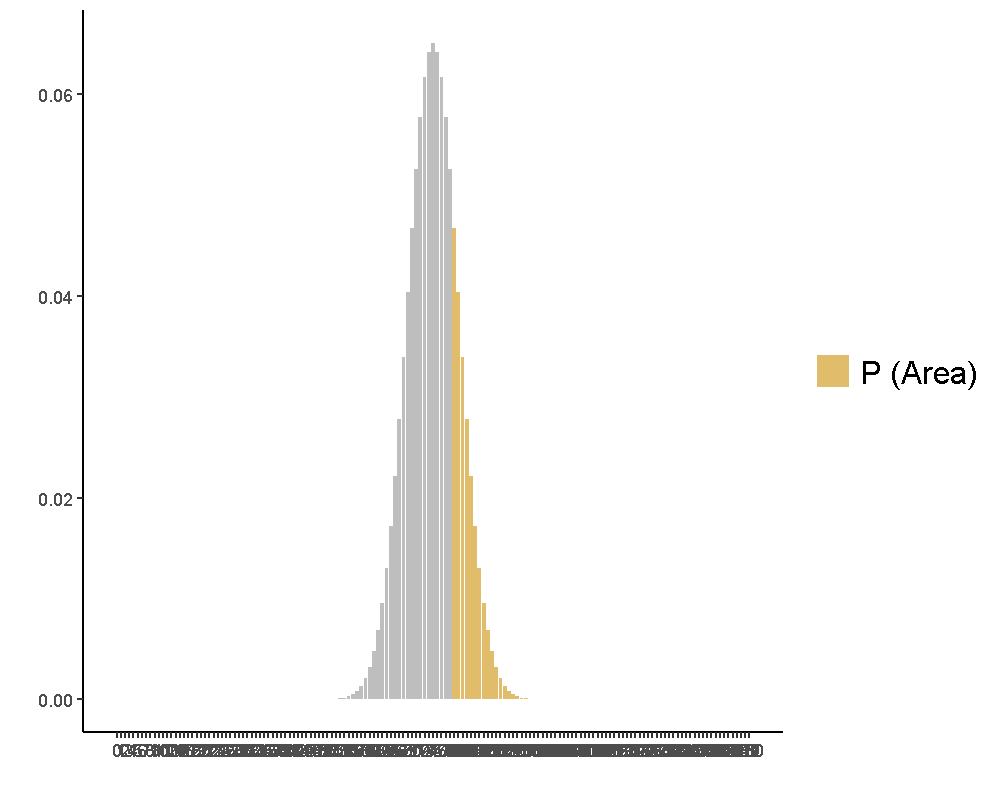
圖 5.6: 單一比率二項檢定之錯誤次數p值視覺化
5.3.3 估計型一錯誤率
在圖5.5與圖5.6,我們標示符合該抽樣分佈平均值與標準差的常態分佈的藍色曲線。即使模擬的常態分佈幾乎貼合理論的常態分佈,讀者必須區分兩者是不同的機率函數。透過常態分佈的機率函數,我們可以取大於平均Proportion1.64個標準差的總計正確次數,是能不接受當下實驗結果屬於虛無假設抽樣分佈一部分的臨界值。這裡展示估計型一錯誤率的方法是計算所有模擬的Proportion數值總數,總計大於這個臨界值的比例。重覆執行jamovi模擬程序示範檔案數次,讀者會發現型一錯誤率估計值在4%到6%之間變化,平均來說將趨近5%。
5.4 單一平均數t檢定
除了所有治療師的答對率,Emily Rosa也可以用每位治療師的平均正確次數做分析。她與父母等人發表的論文是使用個人的正確次數,分析治療師們到底有沒有真本事。以下示範原始論文使用的單一平均數t檢定分析結果。
稍早在單元 5.2 Roland Fisher的下午茶試驗解說中,我們得知Emily Rosa的實驗參考Fisher的設計,因此治療師們如果是靠運氣面對Emily的測試,每個人能做出正確次數的機率,符合一次試驗正確率p=0.5的二項機率分佈。每位治療師進行十次測試,依靠運氣的正確次數期望值就是\(10 \times 0.5 = 5\)。只要符合此期望值,不論治療師進行幾次測試,或招募多少位治療師,都能製造虛無假設的平均正確次數抽樣分佈。
如果Emily認為有本事的治療師應該有80%以上的答對率,我們就可以設定對立假設正確次數期望值是\(10 \times 0.8 = 8\)。招募的治療師確實有此本事的話,Emily不論做多少次實驗,平均正確次數的抽樣分佈之期望值將接近8次。
5.4.1 抜靴法製造模擬樣本
1970到1980年代之間,越來越多採用統計推論進行研究的領域,面臨多數問題不能確認事先確認母群體機率函數甚至期望值的現實。許多樣本模擬方法應運而生,最重要的兩種方法是蒙地卡羅法(Monte Carlo)與抜靴法(Bootstrap)。本書採用抜靴法製造各推論統計單元範例的抽樣分佈,因為這個方法以實際的樣本資訊做為母群體,設定每個樣本平均值的樣本數,即可重覆再抽樣,形成平均值的抽樣分佈。
Emily Rosa的TT測驗是示範抜靴法的良好入門示範。因為虛無假設與對立假設的來源母群體都是二項分佈,我們可以分別製造虛擬的來源樣本數值,再以這些數值製造模擬實驗結果。可發現以此法製造的模擬抽樣分佈,都會遵循中央極限定理,形成以各假設期望值為中心的常態分佈。
運用虛無假設及對立假計的設定,製造一萬次模擬實驗結果,每次有十五筆平均正確次數,累積出如圖5.7的兩套抽樣分佈直方圖。所有模擬實驗的平均數相當接近預設的期望值,但是變異數並不相同。以兩套抽樣分佈的期望值與變異數繪製常態分佈,可發現兩套抽樣分佈都相當接近常態分佈,顯示每位治療師測試結果的平均值,累積而成的抽樣分佈遵守中央極限定理,趨近常態分佈。
圖 5.7: 單一平均數t檢定平均值抽樣分佈:虛無假設(藍色)、對立假設(紅色)、t分佈判斷標準(黑色垂直線)、常態分佈判斷標準(灰色垂直線)
5.4.2 錯誤率估計比較:常態分佈 vs. t分佈
然而我們為何要使用t分佈–而非常態分佈–判斷統計值屬於虛無假設的條件機率?從型一錯誤率估計結果,能得到一些可供解釋的資訊。圖5.7呈現的兩道垂直線,分別代表t分佈與常態分佈預估的判斷標準,運用jamovi示範檔案的模擬程序,得到型一與型二錯誤率的估計值:常態分佈標準估計型一錯誤率約0.051,估計型二錯誤率約0.0019;t分佈標準估計型一錯誤率約0.0275,估計型二錯誤率約0.008。
如果採納一般約定的0.05顯著水準,常態分佈的標準看起來剛剛好,t檢定似乎過嚴。但是這個原則來自約定促成,並沒有考慮真正的機率計算。我們還必須參考一個條件:這是雙尾還是單尾檢定?
5.4.3 p值與型一錯誤率計算起點:雙尾 vs. 單尾
連續隨機變數具備等距性質,因此機率函數可計算大於某量數的累積機率,或者小於某量數的累積機率,還可以總和大於較大量數與小於較小量數的累積機率。這些特性讓我們能根據問題性質,決定採雙尾的判斷標準,還是單尾的判斷標準。
採用雙尾的判斷標準,根據資料計算得到的統計值應視為絕對值,如Emily的實驗結果可能是-1.046,也可能是1.046。p值是分別由負無限大累積到-1.046,以及由1.046累積到正無限大的機率總和。運用jamovi的distACTION,可知jamovi與JASP的t檢定模組,為何算出的p值都是0.313。
採用單尾的判斷標準,必須事先設定得到的統計值小於或大於虛無假設期望值。確認累積機率的計算起點,才能從機率分佈得到符合問題狀況的p值。以-1.046來說,單尾t檢定的p值是0.157。
採用雙尾或單尾判斷標準當然也影響型一錯誤率的估計。已知示範檔案的預設判斷標準是雙尾,總計產生自虛無假設的模擬數據,只與大於這虛無假設期望值的標準比較,所以估計錯誤率越接近0.025者,越符合虛無假設的平均數抽樣分佈。
5.4.4 信賴區間
除了運用假設檢定,母數統計的使用者還可以計算信賴區間(confidence interval),分析當前實驗結果,檢視現在的資料相容虛無或對立假設期望值的機率,與真陰率(\(1-\alpha\))或真陽率(\(1-\beta\))一致的程度。單一平均數t檢定的信賴區間數學表示與R程式碼表列如下:
| 數學 | R |
|---|---|
| \[\bar{y} \pm t_{\frac{\alpha}{2}} \times \frac{s}{\sqrt{n}}\] | t_cv <- qt(alpha,df=DF) lci <- sim_TT0 - t_cv* sim_TT0_sd/sqrt(N) uci <- sim_TT0 + t_cv* sim_TT0_sd/sqrt(N) |
信賴區間與假設檢定一樣,都是長期累積的可能結果。所以Emily的實驗結果,獲得95%CI [-1.017, 0.350],也就是說正確次數5有95%的機率與這次結果相容。\(\alpha\)在假設檢定代表最大的錯誤肯定機率;在信賴區間代表所有可能樣本的區間範圍,有多高比例包括假設的期望值。這個比例是\(1 - \alpha\),因此信賴區間的正式寫法記為%CI。示範檔案的Rj報表最後一行,是總計1萬筆模擬數值的信賴區間,有包括5的總數目。這個數字會隨重新執行不斷變動,但是數字會在9400到9600左右,也就是大約有95%的模擬數值信賴區間,包含代表治療師們只是靠運氣做實驗的平均正確次數。
從模擬程序的圖解可以發現,p值是從逼近的t機率函數取得累積機率。信賴區間與型一或型二錯誤率的估計,則是來自大量模擬數據的累積,也是最接近真實資料的估計方法。因此有學者提倡心理學研究者應該使用信賴區間,而非p值呈現結果(Cumming and Finch 2005)。本書不特別評論那種方法較佳,讀者運用任何方法之前應該思考一個問題:兩種方法都是建立在本質是條件機率\(P(\frac{D}{\theta})\)的抽樣分佈,加上多數情況是根據期望能否定的虛無假設。如果我們想探討真實的\(\theta\)是否與假設相符,累積大量資料之後,假設檢定與信賴區間能給我們多少有意義的資訊?
5.4.5 檢定程序示範
JASP與jamovi都有提供完整的t檢定模組,本書提供的jamovi示範檔案與JASP示範檔案都是以雙尾檢定示範。採取雙尾檢定的理由是Emily Rosa做這次實驗之前,並不明瞭治療師們的答對率有多高,只能假設如果真有本事,就不會亂猜;如果沒本事, 平均答對次數應該等於5。如果TT學會有公佈受訓過的治療師們做類似測試有一定的答對率,Emily使用單尾檢定才有意義。
請者可以自行更改t檢定模組中的test value與單尾/雙尾檢定的設定,比較不同設定的分析結果與模擬數據的差異。和二項檢定相比,t檢定要考慮更周詳的分析條件:如參與者人數,每人的測試次數,平均數能做抽樣分佈期望值之估計等等。如果符合可運用的條件,t檢定提供的錯誤率估計更全面,卻也容易被使用者忽略或誤會。
5.5 總結
二項檢定與單一平均數t檢定的抽樣分佈都是來自一定範圍數值的隨機變數,分派數值之間的出現機率,能產生符合虛無假設或對立假設的抽樣分佈。
母數統計與無母數統計的重要區別是所根據的抽樣分佈性質:母數統計的抽樣分佈之形成必定遵守中央極限定理。
任何抽樣分佈必有一個逼近的機率函數,此機率函數是計算p值的來源。
任何抽樣分佈能用適當的模擬程序產生,模擬的抽樣分佈是估計型一或型二錯誤率的唯一可靠來源。
信賴區間來自模擬的抽樣分佈,任何一次實驗結果的信區間應視為所有可能結果裡,抽樣分佈期望值有多高機率相容於此區間內的任何數值。
5.6 習題
(jamovi模擬程序 Emily Rosa第一個實驗)
(型一與型二錯誤率)
References
Cumming, Geoff, and Sue Finch. 2005. “Inference by Eye: Confidence Intervals and How to Read Pictures of Data.” American Psychologist 60 (2): 170–80. https://doi.org/10.1037/0003-066X.60.2.170.
Fisher, Ronald A. 1966. The Design of Experiments. 8th edition. New York: Hafner Publishing Company.
Lindsay, Stephen, Daniel Simons, and Scott Lilienfeld. 2016. “Research Preregistration 101.” Observer 29 (10): 14–16.
Rosa, Linda, Emily Rosa, Larry Sarner, and Stephen Barrett. 1998. “A Close Look at Therapeutic Touch.” JAMA 279 (13): 1005. https://doi.org/10.1001/jama.279.13.1005.