第8單元 相關與迴歸
這個單元介紹兩個連續變項相關程度的皮爾森相關係數,以及如何計算兩者之間的簡單迴歸。以統計方法的發展歷史來說,相關與迴歸的分析方法比假設檢定還早出現。早在十九世紀,Francis Galton(他的表親是提出演化論的Charles Darwin)測量大量不同人種的感官能力與各式運動反應資料,他把各種資料湊成好幾對,繪製成一系列散佈圖(scatterplot),歸納出第一套計算迴歸係數的方法。他想要運用資料之間的迴歸,分析不同人種之間的差異。儘管理論和研究方法都還不夠成熟,Francis Galton收集與分析資料的方法直接影響智力的研究與智力測驗的發展。
進入大數據時代,資料科學家想做的事情和Francis Galton差不了多少,都是計算一系列變項的相關性,挑出其中最可能預測變項A的變項B,評估兩者迴歸關係的預測能力。在雙變項的世界,變項之間的共同變異(covariance,以下簡稱共變),是表達變項相關的最佳指標。
8.1 案例介紹
相關係數的示範案例採用五大性格特質的真實資料。五大性格由情緒不穩定性(Neuroticism)、外向性(Extraversion)、經驗開放性(Openness)、親和性(Agreeableness)、盡責性(Conscientiousness)等五種主題的測驗題目組成。示範資料來自 Dolan et al. (2009) 收集500位大學新生的施測資料,JASP與jamovi都有收錄這筆公開資料。除了示範如何利用兩種軟體製作符合寫作格式的相關係數表格,jamovi示範檔也提供相關係數抽樣分佈的模擬程序。
簡單迴歸的示範資料來自 Navarro and Foxcroft (2018) 提供的案例。這項案例紀錄一位新手爸爸在小孩出生後一百天裡,小嬰兒的睡眠時間,爸爸的睡眠時間,以及爸爸用0到100分自評的情緒低落程度。本單元將用JASP與jamovi示範,如何算出以爸爸的睡眠時間預測情緒低落程度的簡單迴歸,以及探討迴歸係數的抽樣分佈。
8.2 皮爾森相關
皮爾森相關係數是兩個變項之間的共變數(Covariance),與標準差乘積的相除。設定兩個變項來自的母群體都是常態分佈( \(N(\mu_X, \sigma_X), N(\mu_Y, \sigma_Y)\) ),皮爾森相關係數的公式就可寫成:
\[ \rho_{X,Y} = \frac{cov(X,Y)}{\sigma_X \sigma_Y} \]
如同五大人格特質的測量資料都是由母群體取隨機抽樣的樣本,任兩個人格特質的相關係數在報告中都記為r,以樣本平均數與標準差計算,計算公式是:
\[ r_{xy} = \frac{\sum x_i y_i - n \bar{x} \bar{y}}{(n-1)s_x s_y} \]
圖8.1呈現JASP輸出五大人格特質之間相關係數,讀者可由JASP示範檔或jamovi示範檔了解輸出表格內容的模組設定。我們使用相關係數絕對值最大的盡責性與情緒不穩定性(-0.368),探討相關係數抽樣分佈的特性。
圖 8.1: 五大人格特質:JASP輸出報表。
8.2.1 相關係數的抽樣分佈
JASP與jamovi提供的相關係數範例資料,都有上百筆的觀察值。原因是樣本數不足一百的隨機樣本所累積的抽樣分佈,不會是像常態分佈一樣的對稱分佈,如此一來必定造成型一與型二錯誤率的估計偏差。樣本數不足時需要使用費雪轉換,才能將抽樣分佈轉換為常態分佈。以下費雪轉換公式,可轉換所有來自同一母群體的所有樣本相關係數。轉換後的樣本相關係數平均數會略高於原始平均數,標準誤必接近\(\frac{1}{\sqrt{n-3}}\)。
\[F(r) = \frac{1}{2} ln \frac{1+r}{1-r}\]
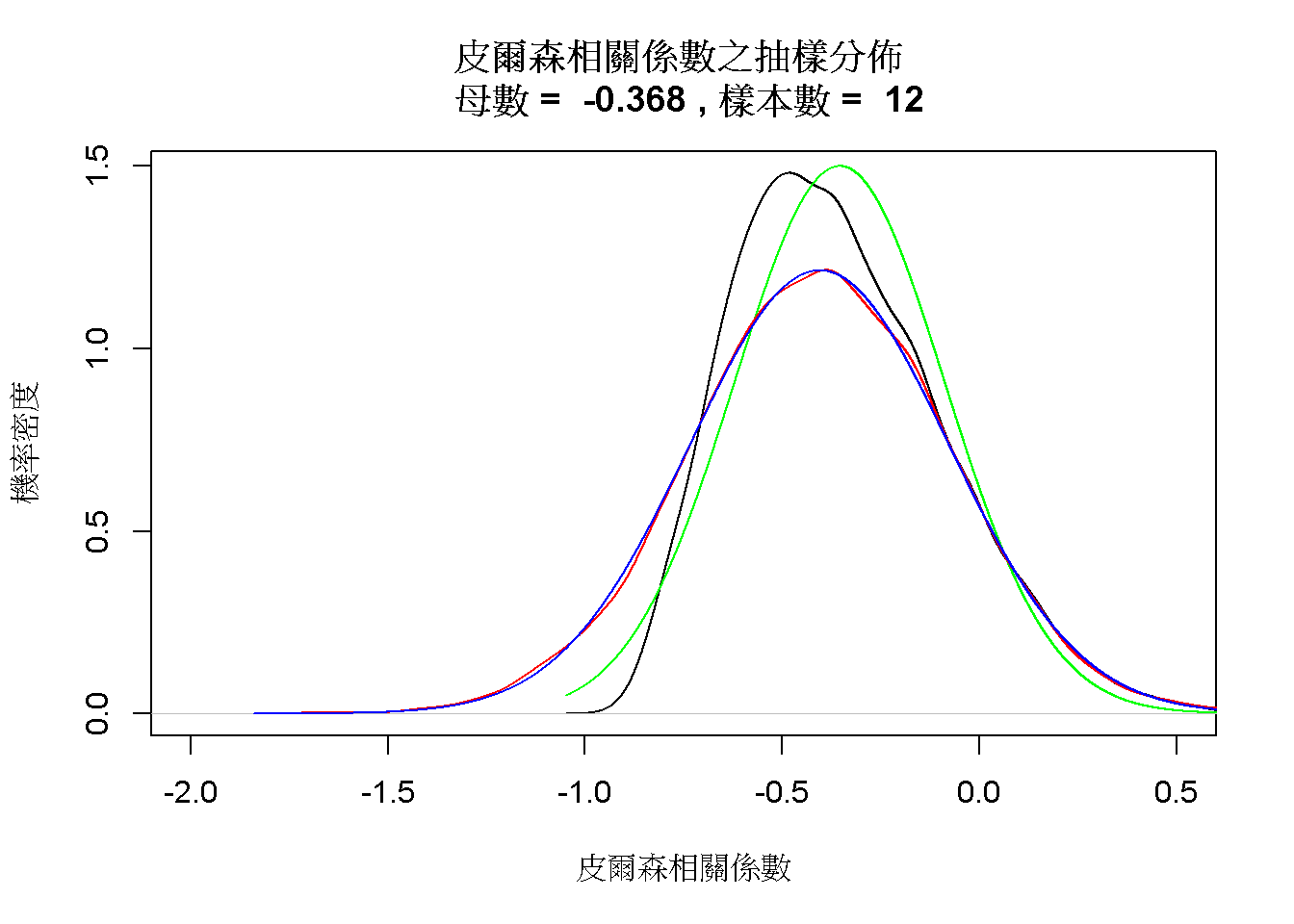
圖 8.2: 設定樣本數為十二位學生,五大人格特質相關係數的抽樣分佈。
以 Dolan et al. (2009) 的五大人格特質資料 為例,如果盡責性與情緒不穩定性相關係數的母群體是\(\rho = -0.368\),只收集12位學生的資料,模擬10000筆樣本相關係數形成的抽樣分佈如同圖8.2呈現負偏態的黑色曲線,與分佈中心是-0.368的常態分佈(綠色曲線)有明顯的差異。10000樣本相關係數經過費雪轉換,形成的抽樣分佈(紅色曲線)與平均數是-0.41及標準誤是0.33的常態分佈(藍色曲線)完全契合,此標準誤相當接近以公式\(\frac{1}{\sqrt{n-3}}\)計算的0.33。
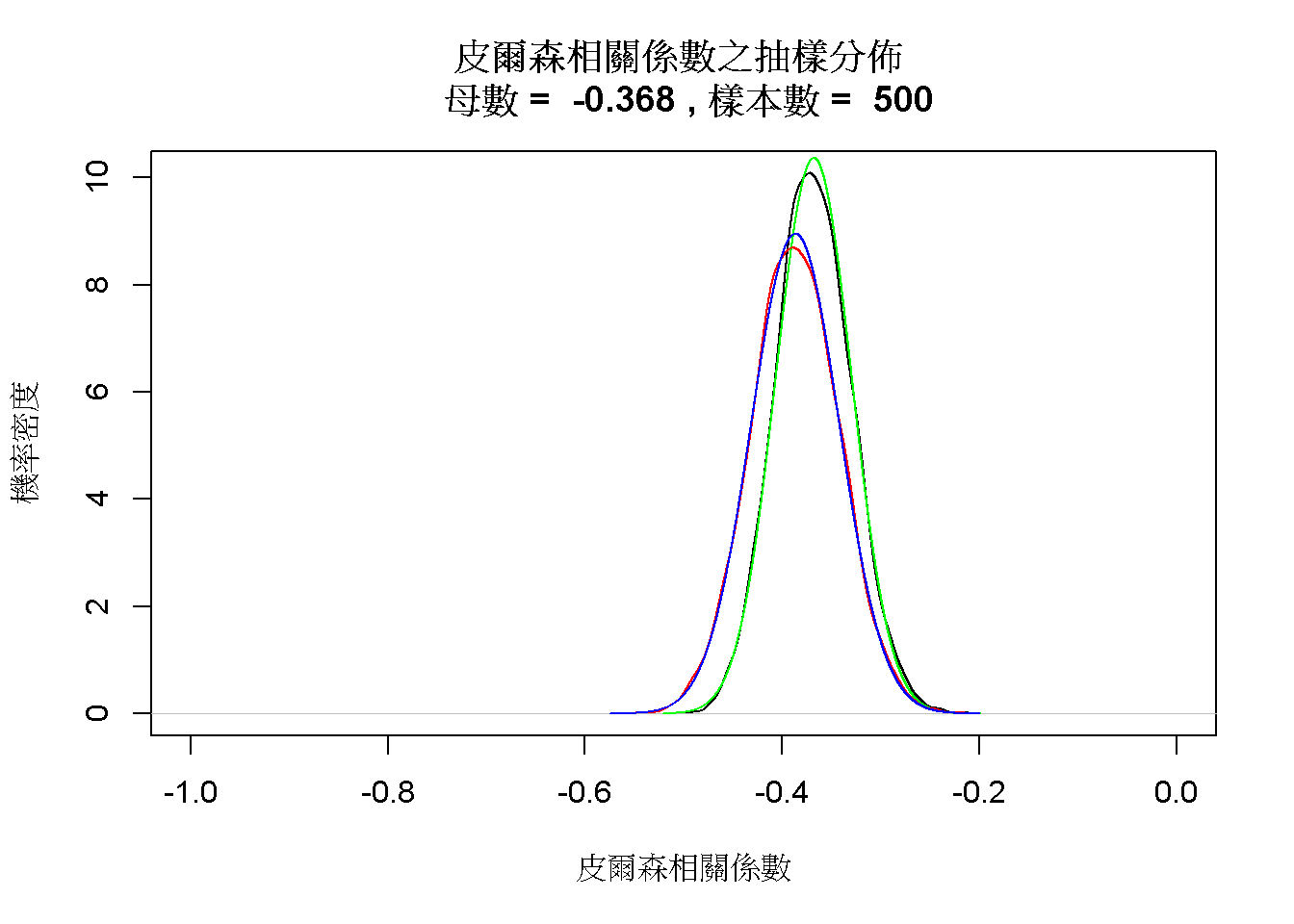
圖 8.3: 設定樣本數為五百位學生,五大人格特質相關係數的抽樣分佈。
將樣本數增加至如至500人,樣本相關係數的抽樣分佈就會契合對稱的機率分佈,如圖8.3代表抽樣分佈的黑色曲線,完全符合抽樣分佈平均數-0.37與標準誤0.04的常態分佈(綠色曲線)。費雪轉轉換後的抽樣分佈(紅色曲線)雖然也符合常態分佈(藍色曲線),但是估計的期望值-0.39明顯不同於母群體。由此例可知,運用相關係數分析資料的研究,要獲得不偏的相關係數估計值,收集的樣本數要達到上百筆。
相關係數的抽樣分佈貝有常態性,所以能運用t機率分佈,以假設檢定或信賴區間分析當下資料估計的相關係數,是否相容於無相關的狀況,即相關係數為0。如果這筆樣本不是來自相關係數為0的母群體,只有相當低的機率出自相關係數為0的抽樣分佈。圖8.4呈現分析相關係數是否為0,對立假設與虛無假設的模擬抽樣分佈。
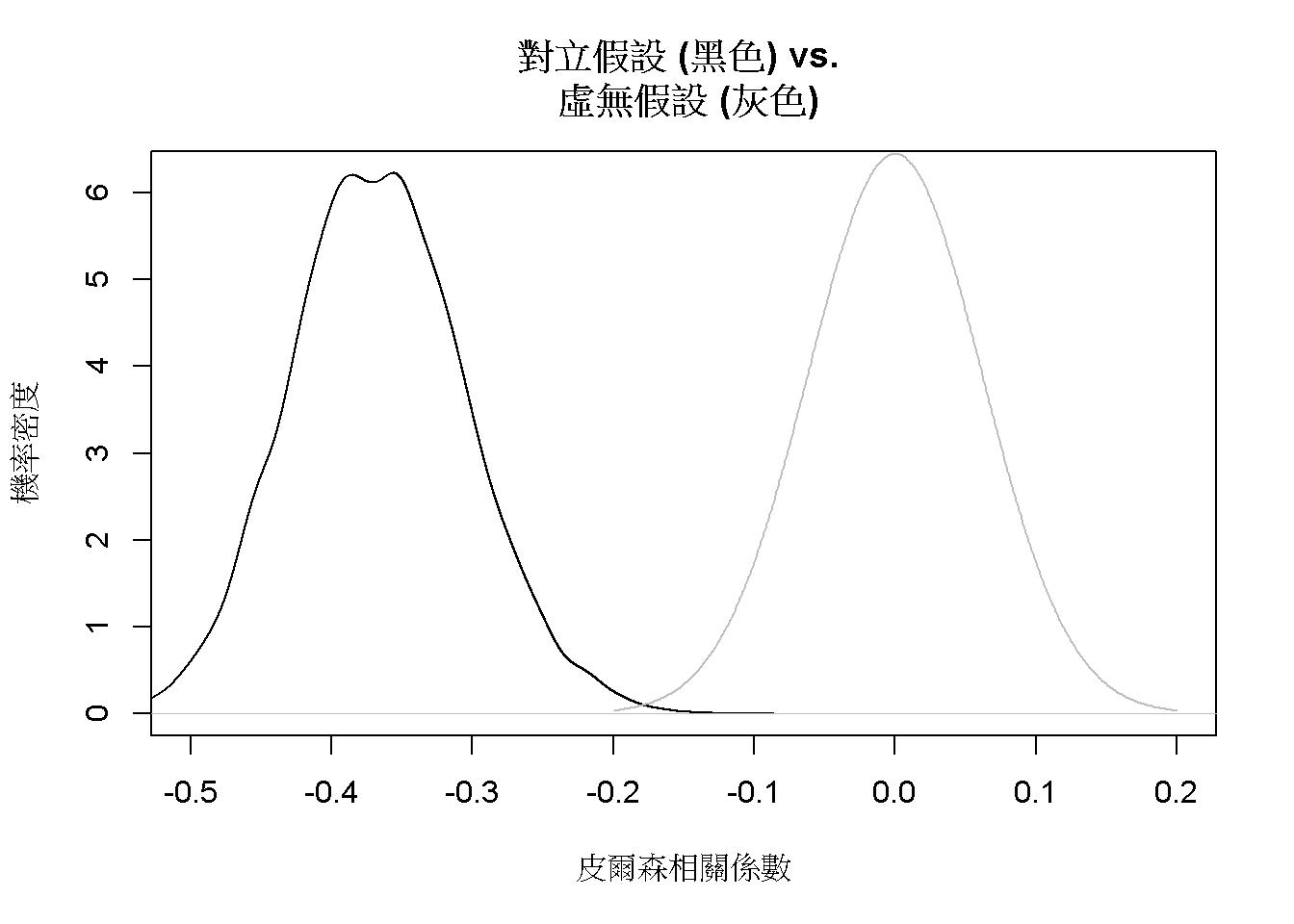
圖 8.4: 樣本數為200,五大人格特質之相關係數是否為0的假設檢定。
8.2.2 相關係數的強度
圖8.4也體現相關係數是一種效果量,所以一次研究得到的相關係數要多高才算理想,必須考慮收集的樣本數。有些統計教材表列所謂的強中弱相關係數,這樣的區分並未考慮樣本數。在此以檢定水準為.05的雙側t檢定為例,圖8.5列出自由度1到100,與可否定虛無假設的最小相關係數。讀者可運用jaomvi示範檔案,自行修改樣本數與檢定水準的p值,察看符合需要的理想樣本數與相關係數。
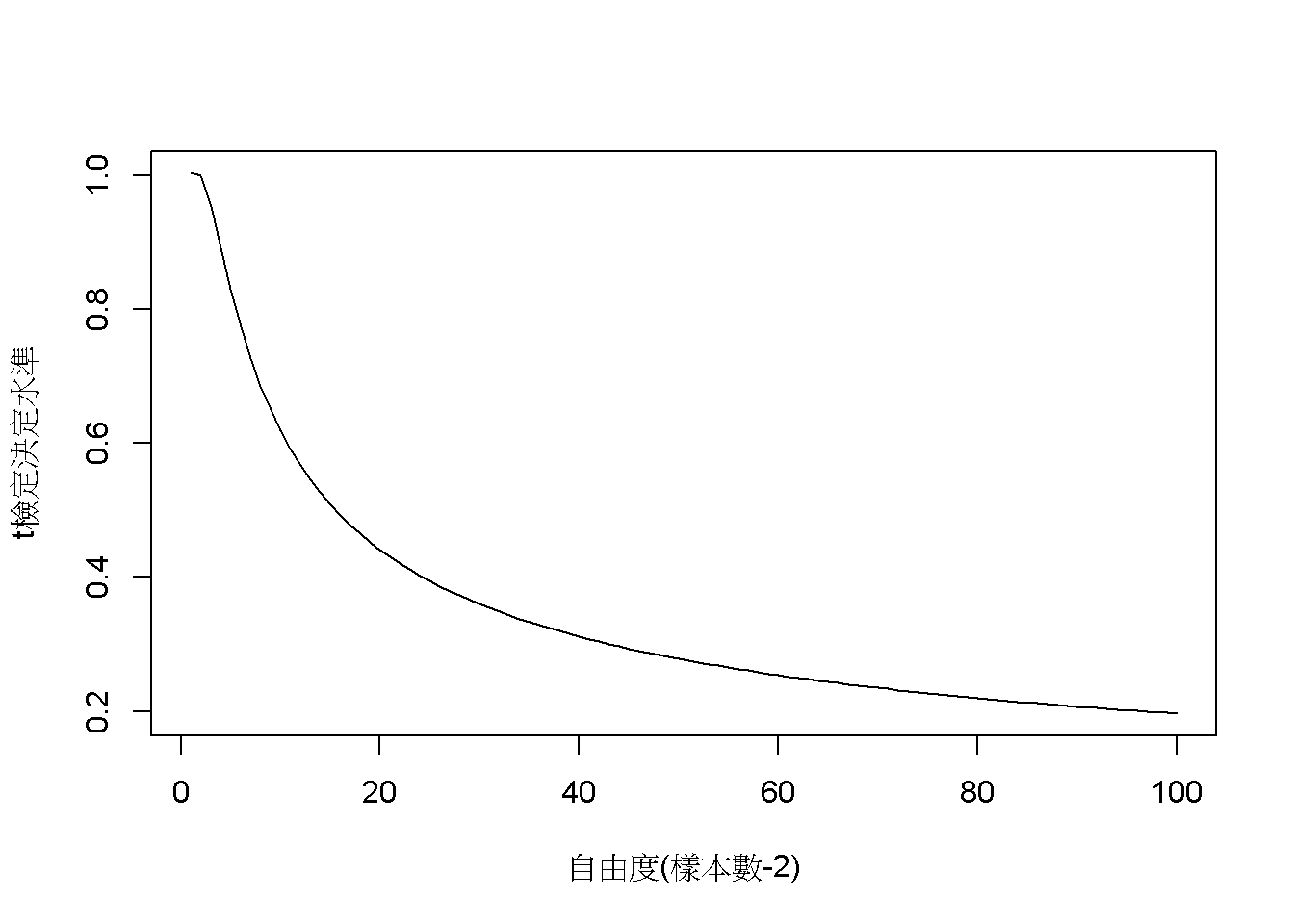
圖 8.5: 檢定水準為.05的雙側t檢定之判斷水準與樣本數(自由度)之變化
8.2.3 相關係數的意義
估計變項之間的相關性通常是一項研究問題的開始,因為發現兩個變項之間存在不為零的相關性,其實有許多意義。圖8.6展示最有可能的五種:自變項與依變項因機遇同時存在(chance);自變項影響依變項的變化(causation);依變項影響自變項的變化(reverse causation);混淆變項同時影響自變項與依變項(confounding);自變項與依變項經過中介變項相互影響(selection;moderation)。
究竟有明顯相關的自變項與依變項是那一種意義?需要進一步研究才能區分。該採取那種研究策略,最好有能引導分辨變項關係的理論,研究者才能掌握最適當的策略。心理科學研究追求的最佳理論,有指引變項之間因果關係的功能,然而任何科學一開始並不會有堅實的理論,需要研究者以清晰的研究設計,收集大量可核實的資料,才能提供更新理論的材料。
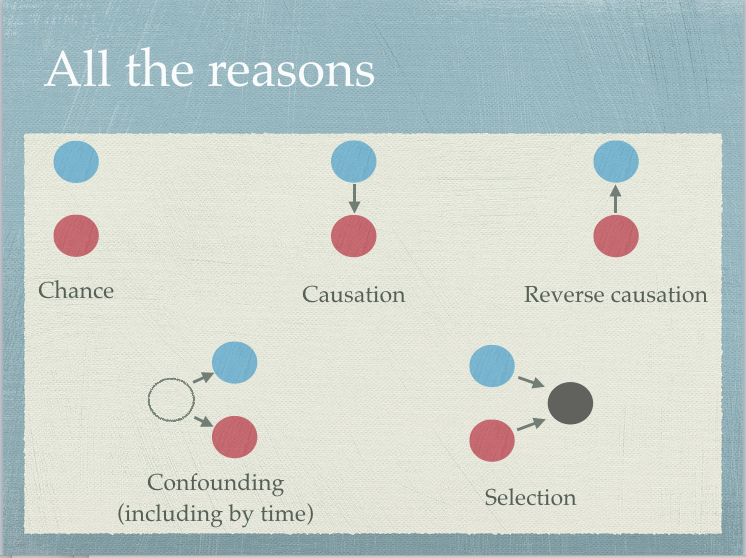
圖 8.6: 相關係數的各種意義。Thomas Lumley提供(推特帳號:tslumley)。
8.3 簡單迴歸
迴歸的重要功能是透過自變項(X)的數值,預測依變項(Y)的觀察而獲得的數值。自變項與依變項資料能形成無限多種線性迴歸關係,有最大預測力的迴歸關係,必然涵括自變項與依變項的平均數,且自變項估計的依變項數值(\(\hat{Y}\))與真實的依變項(Y)數值之差異最小。預測數值與真實數值的差異是以差異平方和總計,所以使用這種方式求得的迴歸關係又稱為最小平方迴歸。簡單迴歸關係的自變項必然與迴歸係數(b)與截距(a)構成線性關係,如同下方的迴歸式。
\[ \hat{Y} = b \cdot X + a \]
如果自變項(X)與依變項(Y)是正相關,截距(a)是以自變項(X)的資料,預測依變項(Y)範圍的最小值,例如圖8.7;如果兩者是負相關,截距(a)是可預測範圍的最大值,例如圖8.8。由此可知迴歸係數與相關係數有密切的關聯,迴歸係數也是一種隨機變數,接著透過範例分析,了解如何運用與迴歸係數有關的參數,評估迴歸關係的預測力。
圖 8.7: 自變項與依變項是正相關的簡單迴歸:以鳶尾花資料庫的versicolor花瓣長度與花瓣寬度為例。
圖 8.8: 自變項與依變項是負相關的簡單迴歸:以鳶尾花資料庫的setosa與versicolor花瓣長度與花萼寬度為例。
8.3.1 範例分析示範
我們使用新手爸爸照顧小嬰兒100天紀錄,運用簡單迴歸以爸爸的睡眠時間預測爸爸情緒低落程度,透過JASP示範檔案與jamovi示範檔案示範如何計算以及擷取報告資訊。JASP使用Regression模組的Linear Regression功能,在設定選單的Dependent Variable匯入dan.grump;Covariates匯入dan.sleep。即可輸出圖8.9的報表:從上面開始第一個表格Model Summary是預設輸出的報告,其中的R(0.903)是自變項與依變項相關係數之絕對值,\(R^2\)(0.816)是依變項的變異可被自變項估計的比例,但是這個數值在簡單迴歸並無明顯功能。第二個報表ANOVA需要於設定選單裡的Statistics勾選Model fit,這份報表報告的內容於稍後單元8.3.3介紹。第三個報表Coefficients需要於設定選單裡的Statistics勾選Estimates,這個報表指出這道直線迴歸的截距是125.96,迴歸係數是-8.937,所以報告中的線性迴歸式是:
\[ \hat{Y} = -8.937 \cdot X + 125.96 \]
迴歸係數與截距都是隨機變數,所以報表有兩項數值是否為0的統計檢定結果;Coefficients報表的另一個重點是Standardized這欄的數值只有自變項,這個數值是標準化迴歸係數,也就是相關係數(-0.903),是以兩個變項資料的標準化分數(\(z_y, z_x\))得到的迴歸關係,所以迴歸線必定通過散佈圖座標軸原點,截距必為0。最後一個Descriptivies報表要勾選設定選單裡Statistics的Descriptives,呈現兩個變項的資料個數、平均值、樣本標準差、與樣本標準誤。情緒低落程度的估計標準誤(1.005)除以爸爸睡眠時間的估計標準誤(0.102),再乘以兩個變項的相關係數(-0.903),就是迴歸係數-8.9。所以簡單迴歸的迴歸係數與相關係數,能運用以下公式相互換算:
\[r_{xy} = \frac{se_y}{se_x} \cdot b\]
圖 8.9: 新手爸爸育兒紀錄簡單迴歸分析:JASP輸出報表。
8.3.2 迴歸係數的抽樣分佈
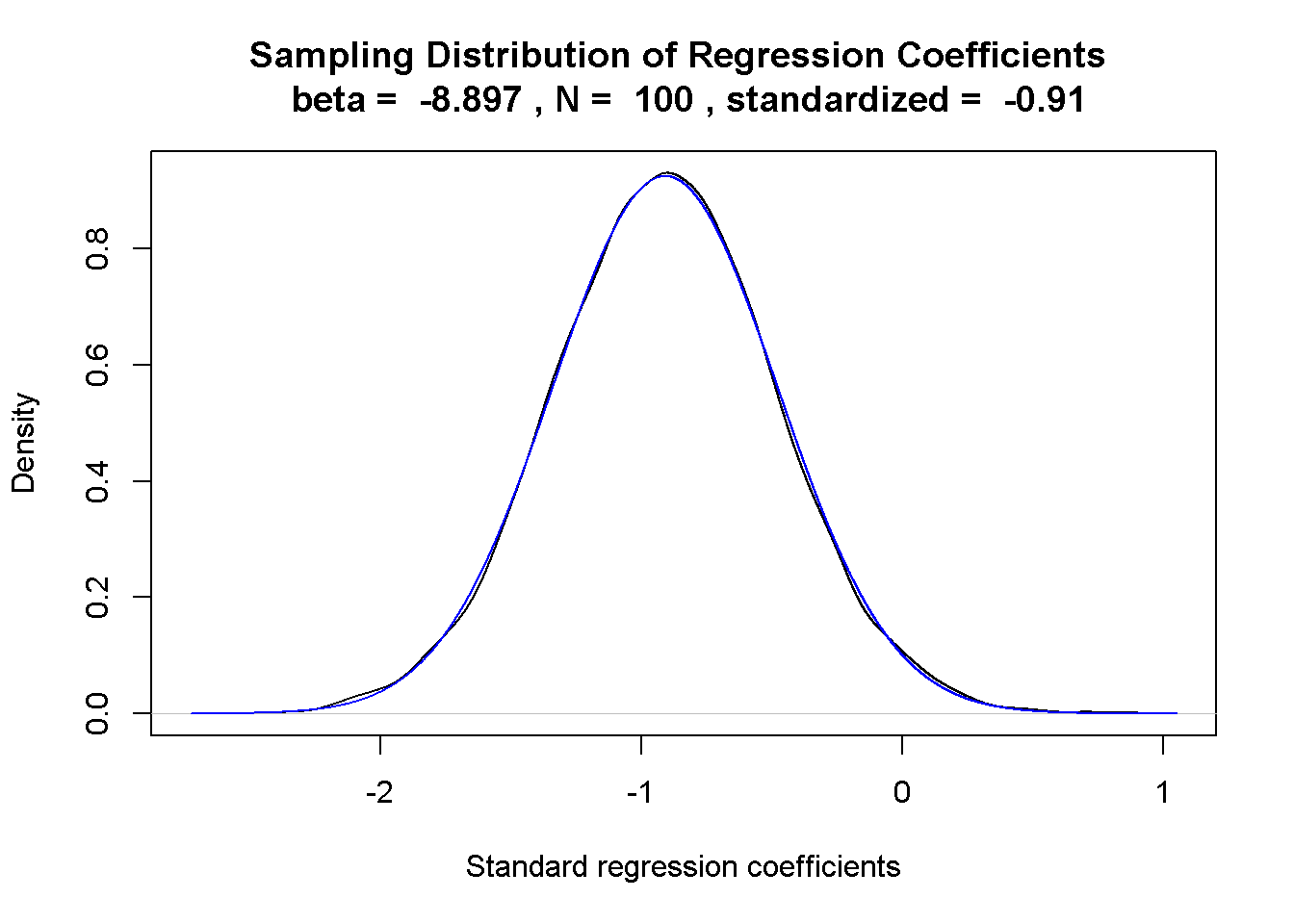
圖 8.10: 樣本數為100,迴歸係數之抽樣分佈。
我們已知迴歸係數也是一種隨機變數,所以只要改裝相關係數抽樣分佈的模擬程序,就能探索迴歸係數的抽樣分佈。在jamovi示範檔案的模擬程序程式碼首四行的設定參數,除了樣本數與相關係數,還有設定自變項與依變項的樣本標準誤。這段模擬程序以新手爸爸的分析結果設定這四個數值,得到圖8.10符合常態分佈的抽樣分佈。這道抽樣分佈的平均數是-0.91,標準誤是0.43,極為接近圖8.9的Coefficients報表報告的標準化迴歸係數,以及自變項的標準誤。讀者可以嘗試改變兩個變項的標準誤,形成的抽樣分佈雖然標準誤會有變化,平均數依然接近標準化迴歸係數。
8.3.3 最小平方法
現在來談談最小平方法的真正意義:有最大預測力的迴歸關係,實際的依變項數值與依變項預測值的差異平方和,是所有迴歸關係之中最小的。首先我們先了解,經由迴歸線得到的依變項預測值,與依變項平均值的差異平方和(\(\sum(\hat{Y} - \bar{Y})^2\)),必定小於實際的依變項數值與依變項平均值的差異平方和(\(\sum(Y - \bar{Y})^2\)),也就是依變項實際資料變異數的分子。前者通常稱為迴歸變異平方和(Sum of Squared Regression,簡記SSR),後者通常程為總變異平方和(Sum of Squared Total,簡記SST)。
SST與SSR之間的差異等於實際的依變項數值與依變項預測值的差異之平方和(\(\sum(Y - \hat{Y})^2\)),這些差異值在統計學中被稱為殘差(residual),總和稱為殘差平方和(Sum of Squared Error,簡記SSE)。除了殘差平方和與迴歸變異平方和的總和必然等於總變異平方和,符合最小平方的迴歸關係,殘差平方和必須小於其他線性迴歸。符合最小平方的迴歸係,也會得到SSR佔SST的比例,等於自變項與依項數的相關係數平方(\(R^2\)),所以這個參數又稱為決定係數。
根據圖8.9的ANOVA報表,可知爸爸育兒紀錄迴歸分析的SST是9998.590,SSR與SSE分別是8159.876與1838.714,讀者可檢視jamovi示範檔案資料的三個計算變項:squared.total,squared.regression,squared.residual,其內皆是各筆資料的差異值平方,運用描述統計模組計算所有差異平方和之總和,確實符合上述數值。
8.3.4 簡單迴歸的信賴區間
在前面的單元裡,我們都有學到計算信賴區間的方法。簡單迴歸的信賴區間是指根據設定的信賴水準(如95%),有多少比例的依變項觀察值,是在迴歸線的預測範圍之內。jamovi線性迴歸模組提供的繪圖選項,能標示信賴區間範圍,如圖8.11的示範。信賴區間的寛度是估計標準誤的倍數,從以下估計標準誤公式可知,正是殘差平方和平均值的開根號。
\[S_{y \cdot x} = \sqrt{\frac{(Y-\hat{Y})^2}{n-2}}\]
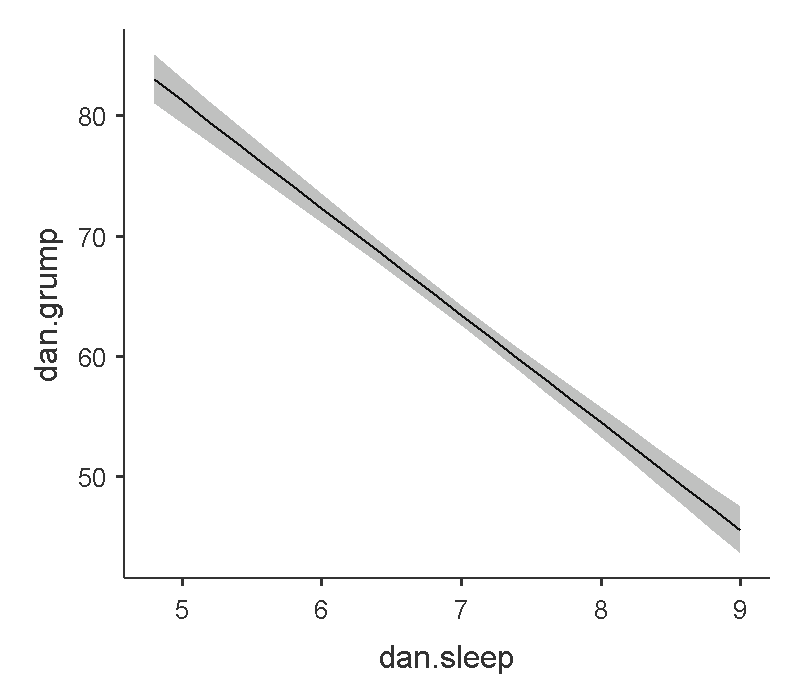
圖 8.11: 新手爸爸育兒紀錄簡單迴歸分析:以jamovi繪製迴歸線與95%估計區間。
8.4 總結
- 相關係數代表兩個變項之間的相關性,其中有多重意義。
- 小樣本資料估計的相關係數通常有偏誤,Fisher校正能使資料符合常態,卻無法修正偏誤。
- 簡單迴歸在測量誤差範圍內,描述依變項數據隨自變項數據變化的趨勢。
- 樣本數足夠時,相關係數與迴歸係數的抽樣分佈都符合常態性,能運用t機率分佈進行假設檢定與估計信賴區間。
8.5 習題
- TBA
References
Dolan, Conor V., Frans J. Oort, Reinoud D. Stoel, and Jelte M. Wicherts. 2009. “Testing Measurement Invariance in the Target Rotated Multigroup Exploratory Factor Model.” Structural Equation Modeling: A Multidisciplinary Journal 16 (2): 295–314. https://doi.org/10.1080/10705510902751416.