第7單元 獨立樣本的推論統計
行為與社會科學研究許多種變項是比較背景接近的兩群人士,在兩種不同情境狀況的行為表現。若研究者使用連續尺度收集資料,適用的資料分析方法就是獨立樣本t檢定。這個單元將介紹無母數統計的獨立性檢定,以及母數統計的獨立樣本t檢定。
7.1 無母數獨立樣本推論統計
本單元示範的獨立性檢定也是運用卡方分佈,判斷各組次數之間的差異有沒有符合預期。不同於單元6.1介紹的McNemar氏檢定,獨立樣本的卡方檢定比較多組觀察次數的比例是否相同?或著是否不同於預期的各組比例?這兩類問題分別稱為適合度問題(goodness of fit)與獨立性/關聯性問題(independence/association)。
以下介紹兩類示範案例,說明計算實際次數與期望次數差異的統計數為何比較符合卡方分佈,以及示範分析程序。
7.1.1 適合度問題案例介紹
有位在網路連載推理小說的作家,撰寫新作品的過程同時經營直播節目,每一集與聽眾討論最新完成的章節。新作品描寫一件兇殺案,故事開始就帶出五位被懷疑是兇手的主角,我們以代號A,B,C,D,E稱之。作家在連載開始就邀請聽眾猜測誰是真兇,並開放聽眾投票。在最後一集揭曉之前,有兩百位聽眾投票,累計結果如下表:
| A | B | C | D | E |
|---|---|---|---|---|
| 58 | 41 | 41 | 42 | 18 |
作家預想他設計的情節引導讀者認為A是真兇,其實E才是真正兇手。你要如何運用推論統計,證實作家的設計達成他的目的?
7.1.2 適合度檢定的抽樣分佈
根據作家的故事設計,作家心中有組最不期待看到的數據:認為是E的觀眾人數,比認為是A的觀眾人數高出一倍以上。將次數換成比例,作家最不期待讀者的票選比例如下表的模樣:
| A | B | C | D | E |
|---|---|---|---|---|
| 0.1 | 0.2 | 0.2 | 0.2 | 0.3 |
以總數200人來說,總計結果會如下表:
| A | B | C | D | E |
|---|---|---|---|---|
| 20 | 40 | 40 | 40 | 60 |
幫助作家分析的你想用適合度考驗,首先要考慮這個狀況能不能使用。適合度考驗的獨變項必是唯一,且為類別變項,如同這個範例的真兇身份。依變項是獨變項各類別的觀察次數(O),在此就是觀眾投人數;同時問題目標能設定明確的期望次數(E),兩者差異的平方才能代表觀察結果與期望結果的差距。適合度檢定的抽樣分佈是以下方統計數公式堆積:
\[\sum\frac{(O - E)^2}{E}\]
堆積而成的抽樣分佈通常接近卡方機率函數,而且自由度決定函數樣態。適合度檢定的自由度等於類別數目減1。而總觀察次數決定觀察次數與期望次數差異平方的變異,進而決定抽樣分佈的範圍,導致型二錯誤率與考驗力的變化。
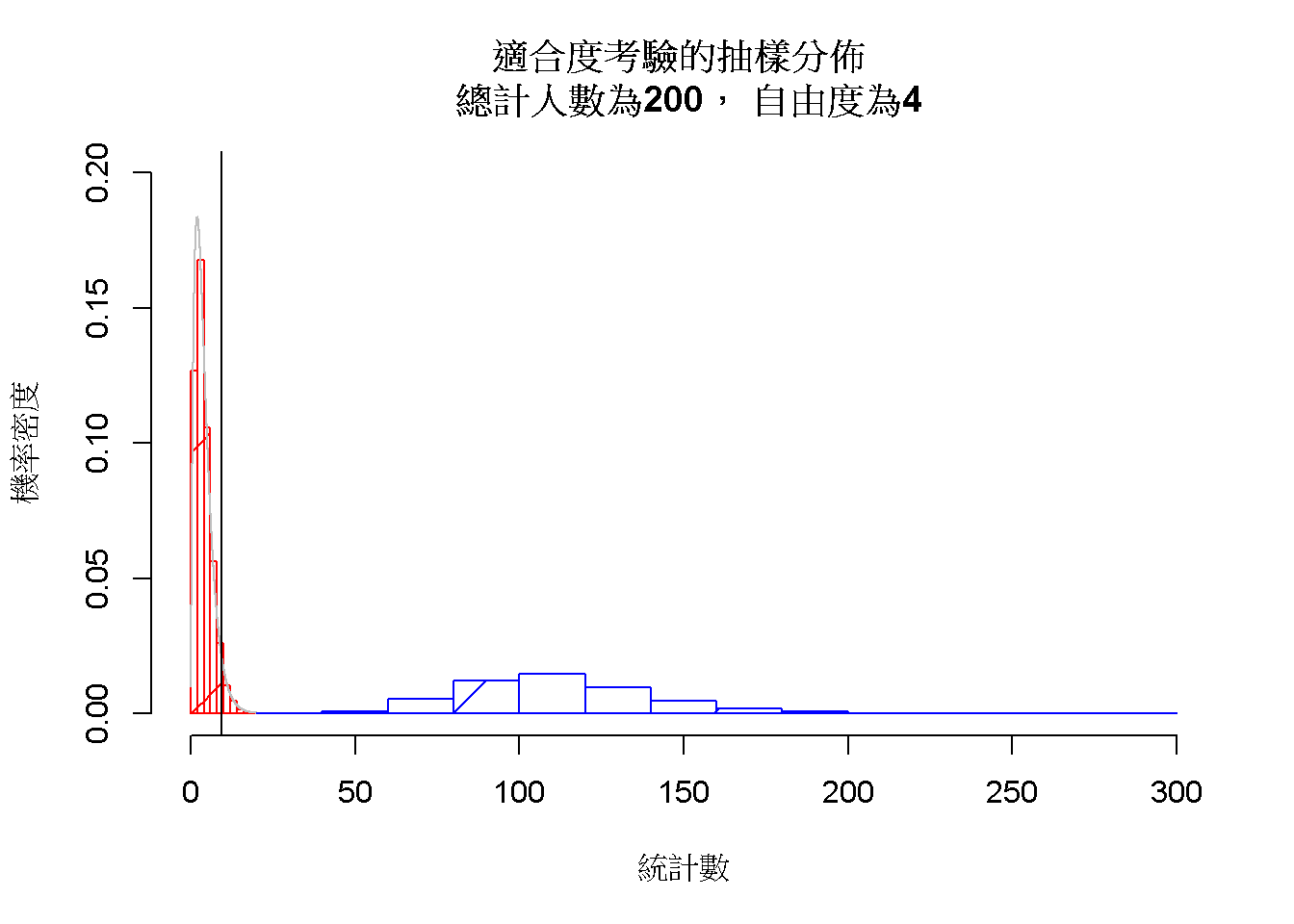
圖 7.1: 適合度考驗的抽樣分佈。 虛無假設(紅)與對立假設(藍)
圖7.1顯現的對立假設抽樣分佈,是與這次投票一致的所有模擬結果,與期望次數的模擬數據之差異構成。與都是期望次數的模擬數據之虛無假設抽樣分佈相比,兩者有頗大的差異,因此型二錯誤率幾乎為零。如果今天作家不期待看到的結果是五位主角投票人數沒有明顯差異,就會發現對立假設抽樣分佈與虛無假設抽樣分佈部分範圍重疊,讀者可自行下載jamovi示範檔案,觀察這種狀況的對立假設抽樣分佈。
圖7.1內的垂直黑線,代表以自由度4的卡方機率函數,判斷水準是.05的統計數9.49。虛無假設抽樣分佈超過此線的比例,代表本範例的型一錯誤率估計值,運用jamovi示範檔案,讀者可發現無論如何改變期望次數的組合,虛無假設抽樣分佈樣態改變幅度不大,型一錯誤率都會維持在.05左右。所以分析者可以根據實際需求,調整判斷水準也能保證認定有差異的結論出錯之機率,不會超過型一錯誤率。
7.1.3 適合度檢定示範
JASP與jamovi的適合度檢定套件各有特色,建議讀者先下載jamovi示範檔案,與JASP示範檔案。跟隨以下說明調整模組選單,了解兩者的差異。
jamovi的適合度檢定模組由Frequencies -> N outcomes開啟。圖7.2的設定選單輸入資料中的兩個欄位Options與Observed Frequency,如果所有聽眾的選擇並未總計,只要置入Options。此例作家不期待的結果,只要操作Expected Proportions,改變五位主角的相對比例,就能得到分析結果。
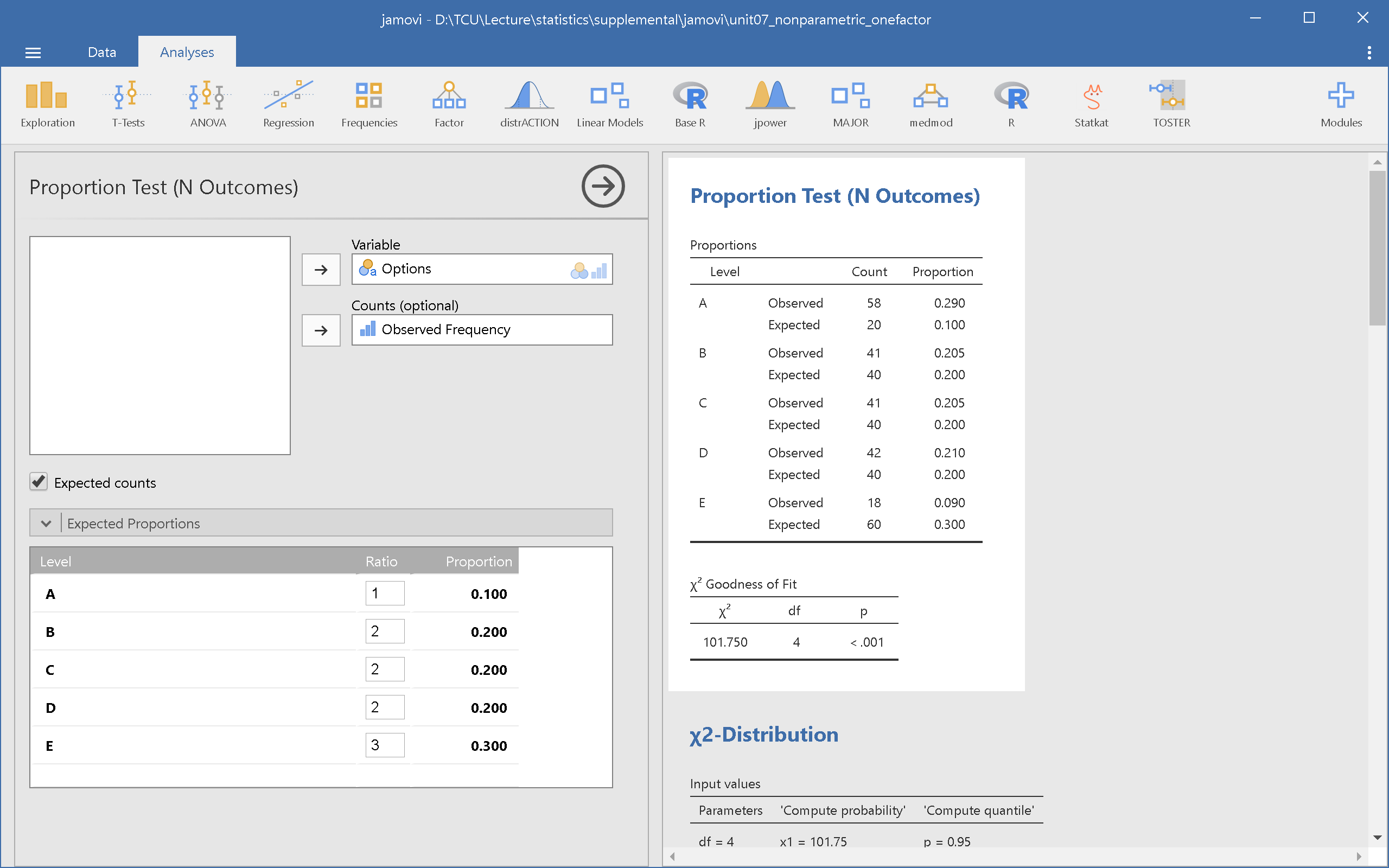
圖 7.2: jamovi適合度考驗操作示範
JASP的適合度檢定模組由Frequencies -> Multinomial Test開啟。圖7.3的欄位設定和jamovi完全相同,不同處是之下的Hypothesis可選擇Multinomial Test與$\chi^2$ Test兩種之一。期望次數是輸入次數決定,並提供信賴區間等計算。JASP適合度檢定的信賴區間提供每一格實際次數的估計範圍,因此本例將區間百分比調整為99%,增加估計的標準。從圖7.3的柱狀圖可見,認為是主角A的人數遠高於20;認為是主角E的人數遠低於60。
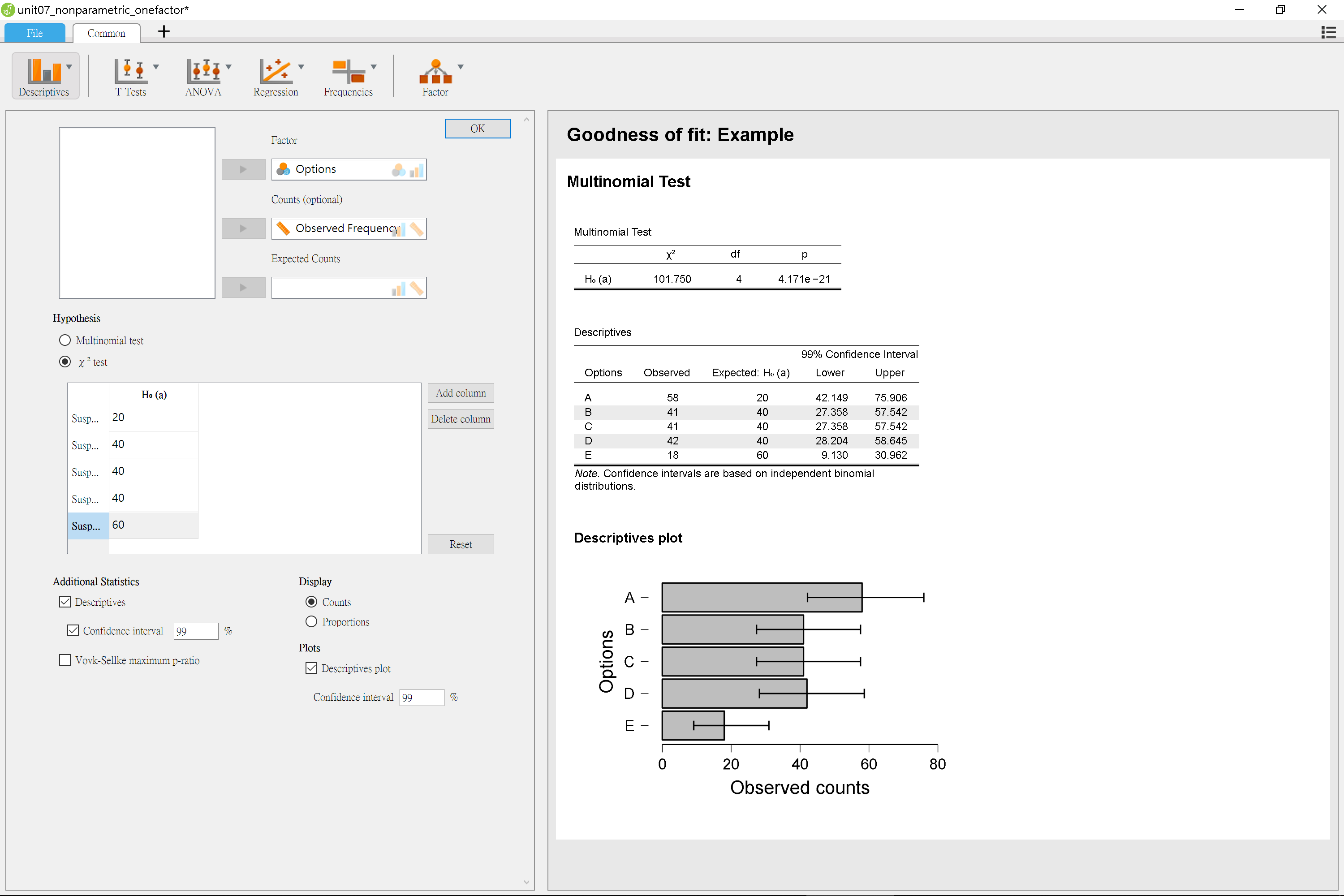
圖 7.3: jamovi適合度考驗操作示範
7.1.4 獨立性問題案例介紹
Seo等人(2007)調查1,184位美國中西部大學生平常從事的運動強度(低度、溫和、劇烈;Low, Moderate, Vigorous),與日常攝取水果數量(少量、一般、超量; Low, Medium, High)之間的關係。研究者認為兩種條件之間並非無關,所以一開始分析工作,先使用卡方檢定確認之,再計算相關係數。
這份資料收錄於JASP的資料庫,讀者可從JASP檔案選單,開啟Data Library -> 5. Frequency -> Health Habits,取得JASP示範檔或原始資料。
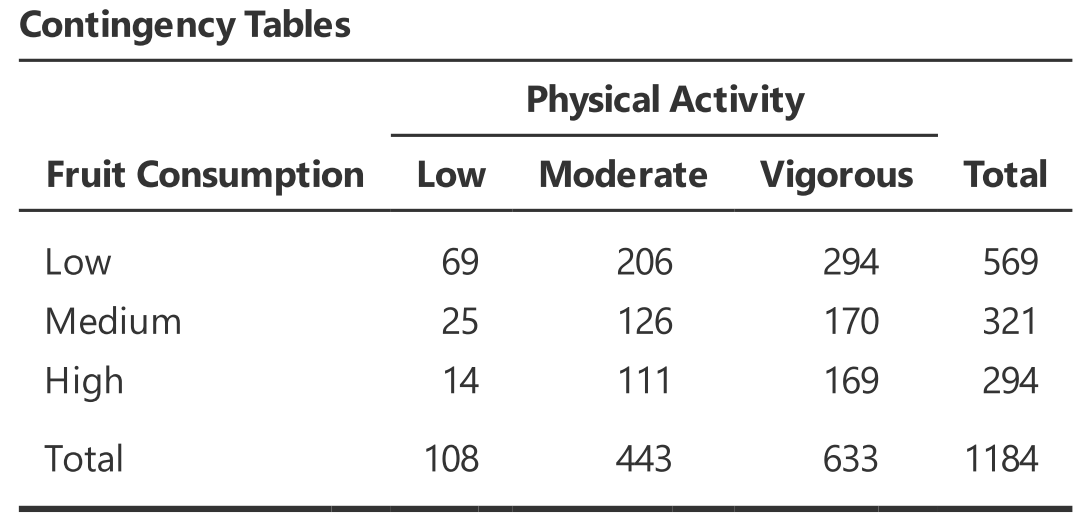
圖 7.4: 美國大學生平常從事的運動強度與日常攝取水果數量
7.1.5 獨立性檢定的抽樣分佈
我們在jamovi示範檔案設計上述範例的抽樣分佈模擬程序。圖7.4列出的列聯表除了各類表觀察次數,還有各欄與各列的總和,各細格元素如下表所示:
| 低度 | 溫和 | 劇烈 | 列總和 | |
|---|---|---|---|---|
| 少量 | \(O_{11}\) | \(O_{12}\) | \(O_{13}\) | \(R_1\) |
| 一般 | \(O_{21}\) | \(O_{22}\) | \(O_{23}\) | \(R_2\) |
| 超量 | \(O_{31}\) | \(O_{32}\) | \(O_{33}\) | \(R_3\) |
| 欄總和 | \(C_1\) | \(C_2\) | \(C_3\) | N |
這項範例的抽樣分佈來自兩個預設彼此無關的問卷題目:運動強度、日常攝取水果數量。兩者都是類別變項,各題選項的選擇人數是各類別觀察次數(O),由列聯表的列總和與欄總和,可計算兩個問題彼此無關的期望次數(E),公式如下:
\[E_{ij} = \frac{R_i \times C_j}{N}\]
與適合度分析相同,每次研究結果的觀察次數與期望次數之差距平方和,堆積任可可能結果的抽樣分佈。
\[\sum_i \sum_j \frac{(O_{ij}-E_{ij})^2}{E_{ij}}\]
根據範例列聯表的欄列總和比例,運用拔靶法,製造兩個獨變項之間有關聯(對立假設)的抽樣分佈,與兩個獨變項之間沒有關聯(虛無假設)的抽樣分佈。模擬結果如圖7.5的抽樣分佈。
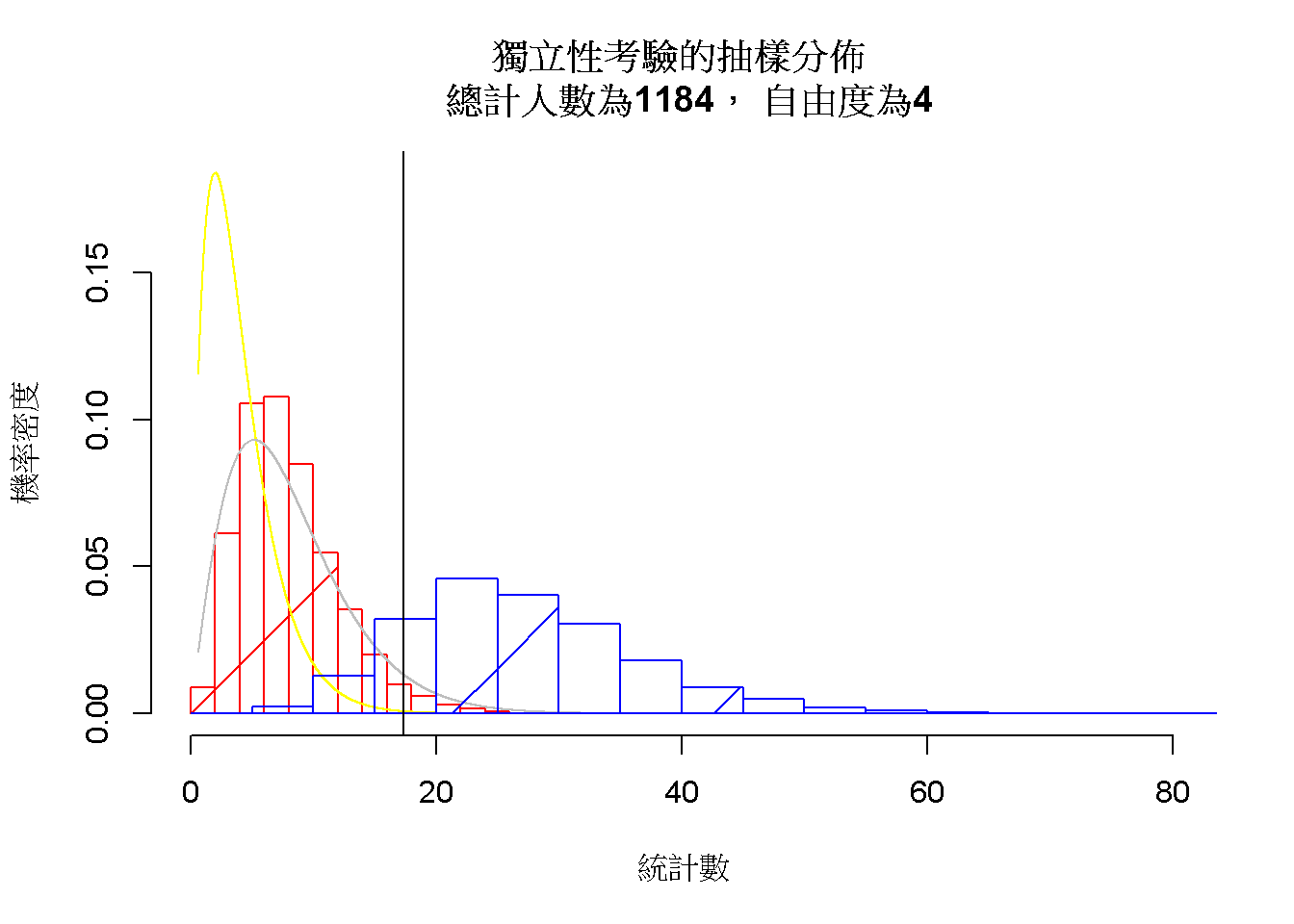
圖 7.5: 獨立性考驗的抽樣分佈。 虛無假設(紅)與對立假設(藍)
模擬顯示兩件獨立性檢定的不同之處。第一是自由度,由於有兩個獨變項,根據計算的機率所學,任何獨變項與依變項的組合都是一種隨機變數,都有一個要被估計的期望值,所以本範例的兩個獨變項各自的自由度是\(3 - 1 = 2\)。兩個獨變項對應的依變項都是同一批觀次數,造成相依的關係,因此自由度是\(2 \times 2 = 4\)
第二是抽樣分佈並不相容一般卡方機率函數。卡方機率函數的期望值即自由度,如圖7.5顯示的黃色曲線;另一條灰色曲線是非中心化卡方機率函數10,期望值是自由度與非中心參數(\(\lambda\))的總和。以.05設定的決定水準來看,一般卡方機率函數估計的型一錯誤率約0.30,非中心化卡方機率函數估計的型一錯誤率約0.025。相對地,一般卡方機率函數估計的型二錯誤率約0.01,非中心化卡方機率函數估計的型一錯誤率約0.15。
許多類似本書示範的JASP與jamovi套裝統計軟體,並未內建非中心化卡方機率函數的計算功能,都是以一般卡方機率函數計算所有卡方檢定的p值。因此建議讀者使用套裝統計軟體分析獨立性檢定,搭配其他相關係數的計算。
7.1.6 獨立性檢定示範
圖7.6與圖7.7示範jamovi與JASP的操作設定,jamovi示範檔案請點此下載,JSAP示範檔案可由官方檔案庫直接取得。
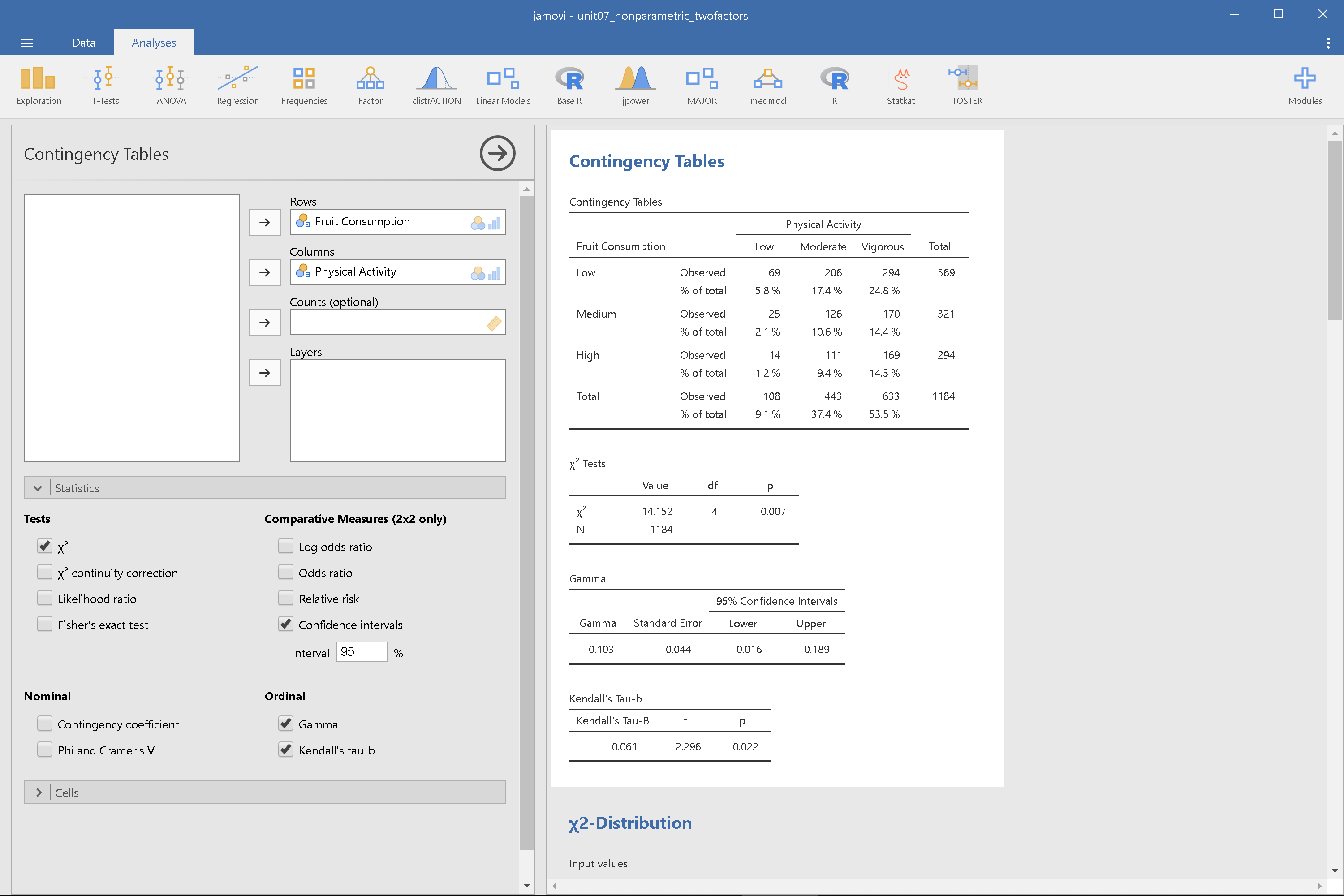
圖 7.6: 卡方檢定獨立性考驗操作設定示範:jamovi
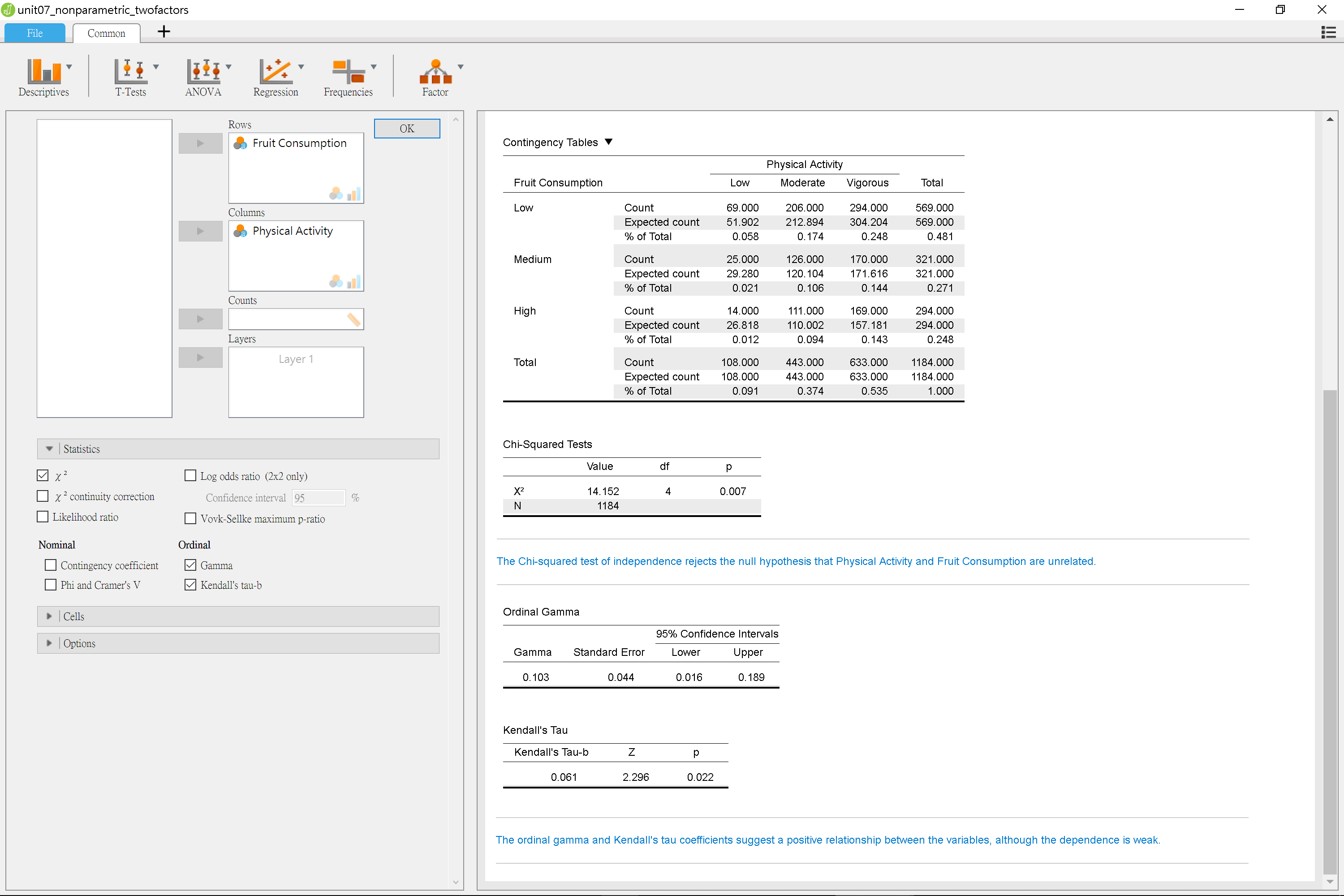
圖 7.7: 卡方檢定獨立性考驗操作設定示範:JASP
請讀者留意以上示範同時計算兩件次序變項相關係數:Gamma與Kendall’s \(\tau\)。為保障p值小於決定水準的獨立性檢定有可信度,建議報告同時說明相關係數的分析,如以下示範:
根據.05的判斷水準,1184位大學生平常運動強度與攝食水果的總量,應該有關聯性,卡方檢定顯示\(\chi^2\)(4, N=1184) = 14.152, p = .007。相關係數分析也支持一致的結論,Kendall’s \(\tau\) = 0.061, p = .022。
7.2 獨立樣本t檢定
獨立樣本t檢定是行為科學研究最常見的分析方法,也是本書第一個要模擬兩個抽樣分佈進行解說的方法。因為兩個樣本分別來自不同的樣本分佈,一般統計教材使用獨立樣本t檢定介紹效果量與考驗力,但是少有教材運用模擬程序解析其中的關係。我們將延續單元6.3的課題,探討樣本數、效果量與考驗力的關係。
7.2.1 獨立樣本平均數案例介紹
這裡採用JASP開發團隊執行長Wagenmakers與同事們(2015)嘗試再現德國社會心理學者Topolinski與Sparenberg(2012)的體現認知實驗,公開資料做為獨立樣本t檢定的示範。Topolinski與Sparenberg的實驗是請參與者來實驗室進行12題開放態度量表,題目內容像是「我經常嘗試新奇的外國食物」。參與者以五點量表表達自己對題目主題的開放程度(-2:非常不同意;2:非常同意)。實驗室環境安排如圖7.8,102位參與者答題時要依指示捲動面前的衛生紙捲,其中48位以順時針方向轉動(clockwise),另外54位以逆時針方向轉動(counter-clockwise)。

圖 7.8: Wagenmakers等人(2017)再現Topolinski與Sparenberg(2012)體現認知實驗的現場設置。
Topolinski與Sparenberg假設大多數可轉動的工具,開啟方向都是順時針,以順時針方向捲動衛生紙卷的參與者,回答開放態度量表的問題,給的評分應該比逆時針捲動的參與者高。原始研究確實發現顯著較高分的結果,再現研究結果則存放於JASP的示範資料集Kitchen Rolls。
Wagenmakers決定執行研究之前,只有Topolinski與Sparenberg發表的結果,無法確定這次結果會不會一樣,因此適合以組間差異尚待確認的觀點,設定判斷水準。兩組平均數經過假設檢定與信賴區間的分析,可能的結果會是:
如果捲動衛生紙捲的方向會影響參與者的開放態度,兩組平均數的差異雙尾t檢定應該出現小於.05的p值,而且95%信賴區間不會包括0。
至於兩組變異數,嚴謹的分析會鑑定有沒有違反變異等量假設與常態分佈假設的標準,再決定要採用的t檢定策略。JASP與jamovi等統計軟體的獨立樣本t檢定模組,都有附Levene檢驗與Shapiro-Wilk檢驗,讓使用者以假設檢定檢視要分析的資料有無違反。未違反假設的資料,檢驗結果的p值必定大於.05或更高的標準。我們可以運用假設檢定的作業原則,設定分析資料未違反兩種假設的判斷水準:
(1)如果兩組資料符合變異等量假設,Levene檢驗的p值應該大於.05。(2)如果兩組資料符合常態分佈假設,Shapiro-Wilk檢驗的p值應該大於.05。如果任何一項出現小於.05的p值,必須在報告中討論。
獨立組比較研究通常希望收集的資料各組樣本數目相同,但是通常不能盡如人意。如果資料不違反變異等量假設與常態分佈假設,自由度必是兩組總人數減2(n1 + n2 - 2),因為各組各有要估計的期望值。計算統計數的標準誤,等於兩組資料的合併標準差(pooled standard deviation)以樣本數加權。如以下公式:
\[s_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}\]
\[s_p = \sqrt{\frac{(n_1 - 1) \times s_1^2 + (n_2 - 1) \times s_2^2}{n_1 + n_2 - 2}}\]
如果資料違反變異等量假設,建議使用變異數不相等的t檢定方法。JASP與jamovi設定選項中的Welch,就是執行此版本的t檢定選項。
7.2.2 獨立樣本平均數的抽樣分佈
比照單元6.2.2,我們設計獨立樣本平均數t檢定的模擬程序,解說為何假設檢定的計算假設檢定的p值與信賴區間,是採用t機率分佈。模擬程序原始碼可參考jamovi示範檔案。
同樣使用拔靴法製造模擬數據,比起單元5與單元6,此次一開始要分別製造兩批模擬數據,再合成代表兩組有差異的抽樣分佈(對立假設),與兩組無差異的抽樣分佈(虛無假設)。首先檢視順時針組與逆時針組的資料範圍,如圖7.9所示。
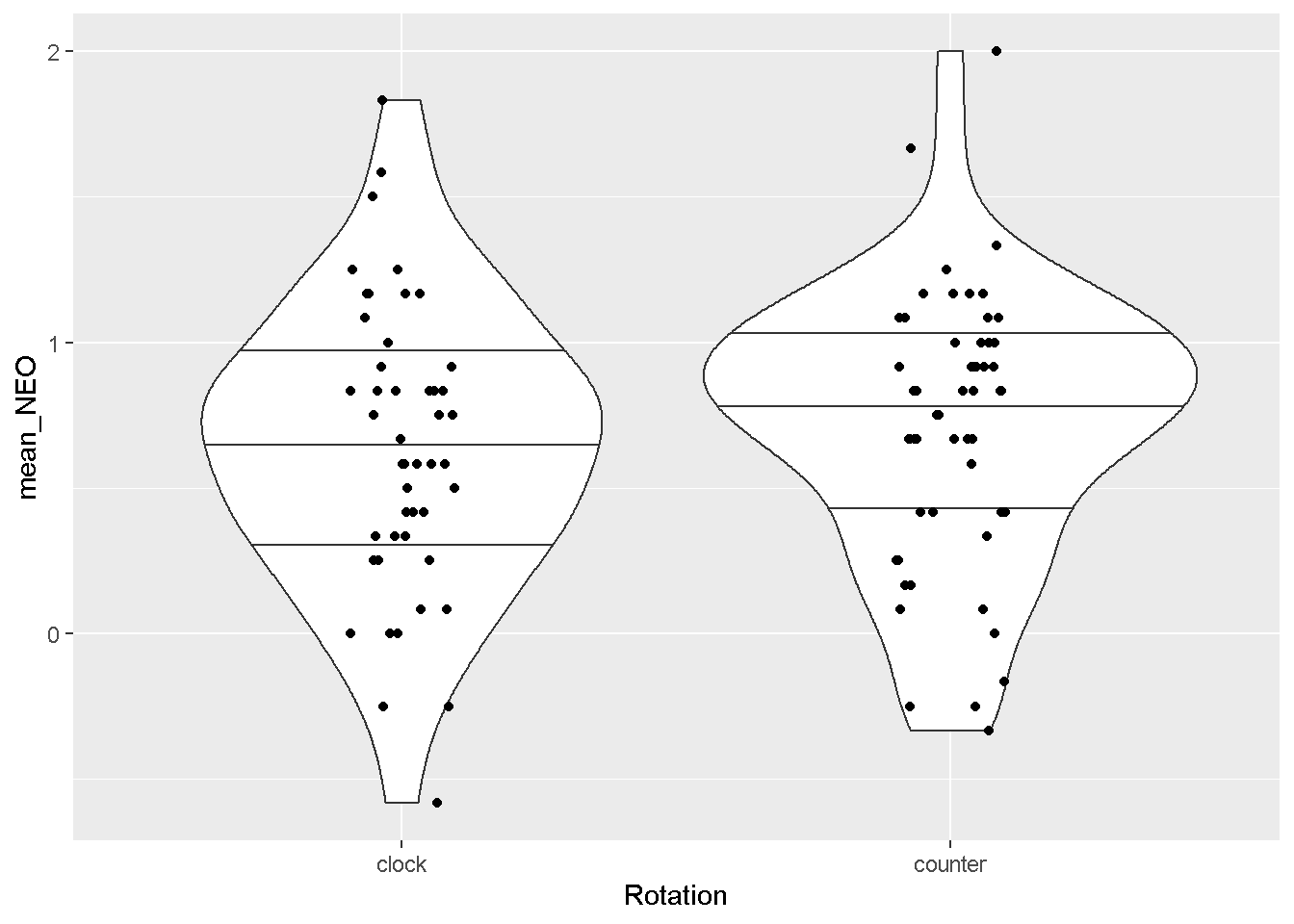
圖 7.9: kitchen roll研究資料分組資料
順時針組的評分平均值為0.64、樣本標準差為0.5;逆時針組的評分平均值為0.71、樣本標準差為0.47。根據原始資料,使用拔靴法分別製造兩批各10000筆模擬平均數,形成圖7.10的平均數抽樣分佈,可見模擬平均數抽樣分佈的平均值近真實資料的統計值,模擬分佈的樣本標準誤是真實資料樣本標準差的\(\frac{1}{\sqrt{48 }}\)與\(\frac{1}{\sqrt{54 }}\)。
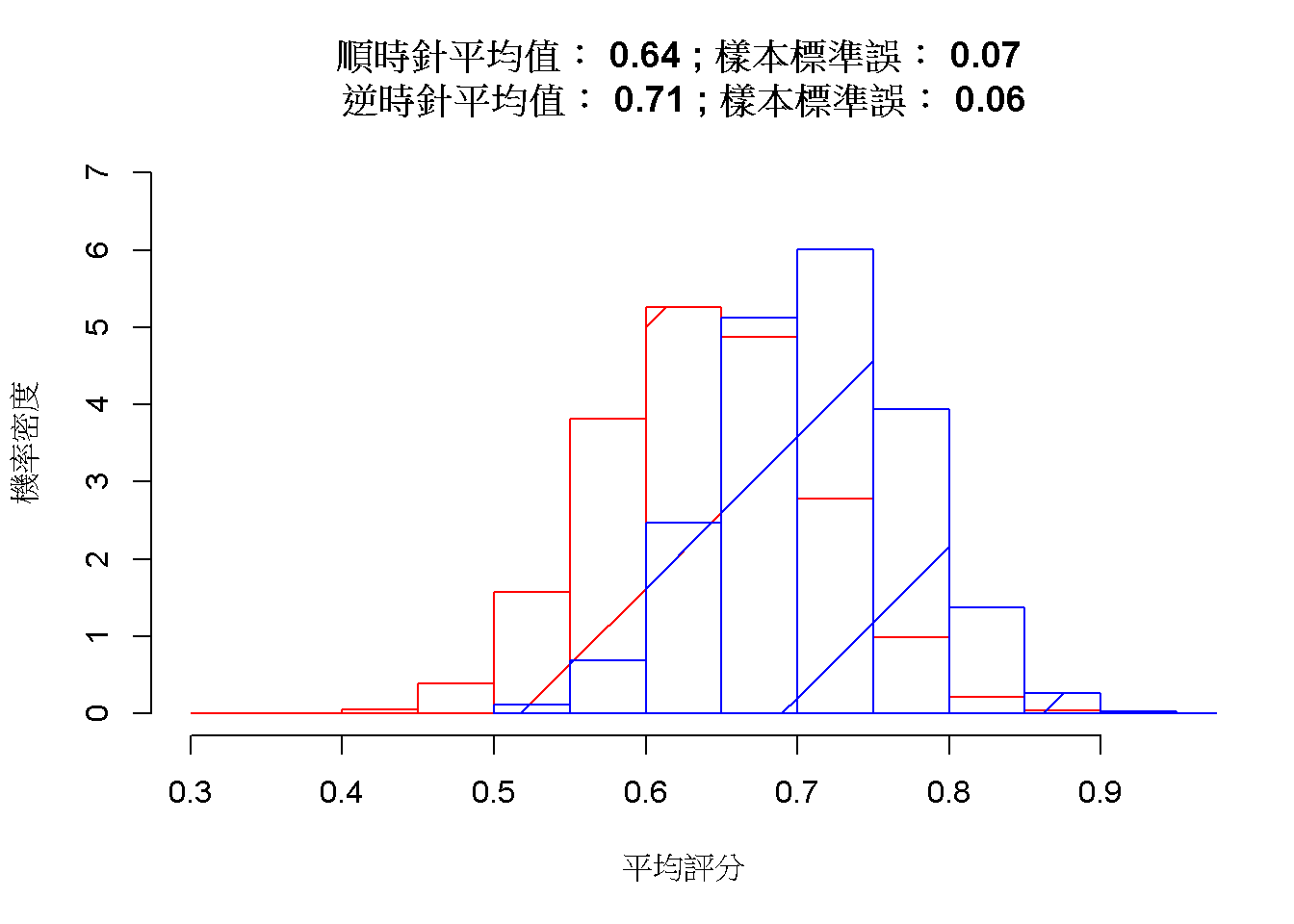
圖 7.10: 順時針(紅色)與逆時針(藍色)的樣本平均值抽樣分佈。
兩組的合併標準差為0.484,加權標準誤為0.096,接近圖7.11的對立與虛無假設抽樣分佈標準誤。
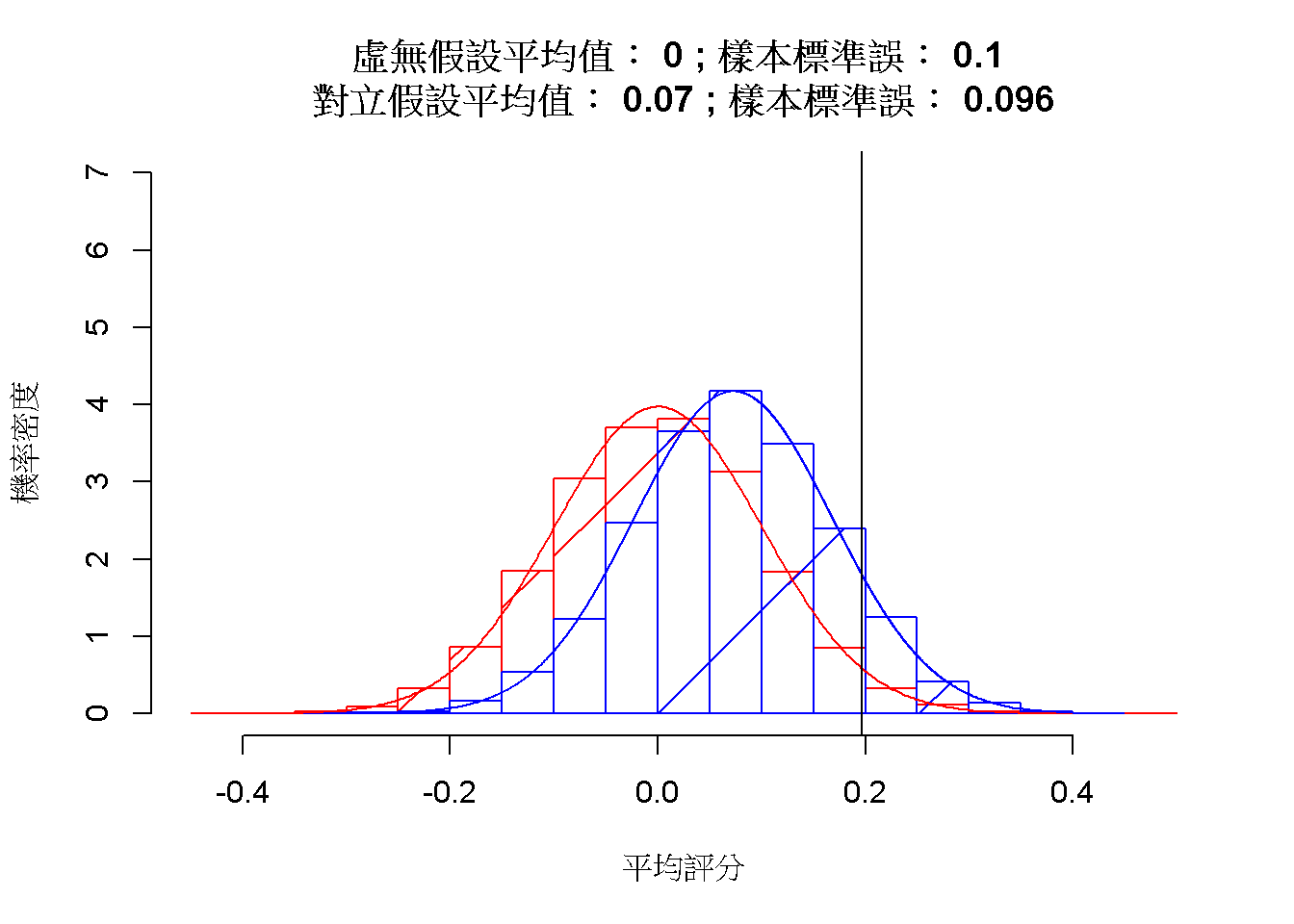
圖 7.11: 平均值差異的5抽樣分佈:虛無假設(紅色)與對立假設(藍色)
兩種抽樣分佈皆符合常態分佈,以雙尾檢定的判斷水準.05為界,估計型一錯誤率為0.026,型二錯誤率為0.903。模擬數據的剖析確定這筆資料符合常態分佈假設,可採用變異等量t檢定分析策略。除了估計的型一錯誤率接近判斷水準,更值得注意的是型二錯誤率估計高達0.9。因為這筆資料是重現他人研究,值得探究這份研究低考驗力的原因。
7.2.3 示範檔案操作與報告
這項研究的獨立樣本t檢定分析可參考jamovi示範檔案與JASP示範檔案。JASP與jamovi的示範畫面請參考圖7.12與圖7.13。
圖 7.12: JASP獨立樣本雙尾t檢定分析操作設定示範。
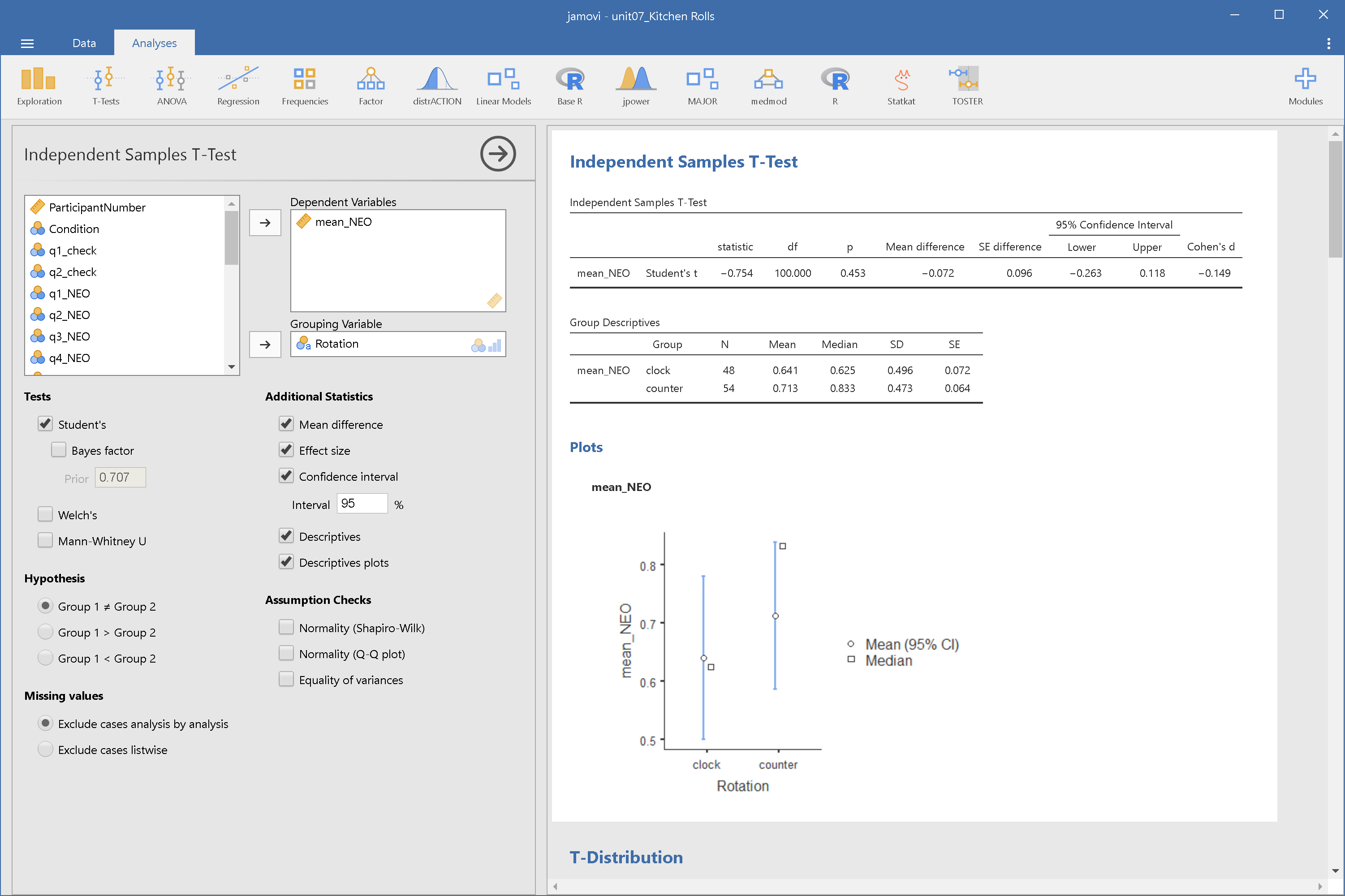
圖 7.13: jamovi獨立樣本雙尾t檢定分析操作設定示範。
這次實驗沒有發現顯著差異,如果是傳統的教學或研究習慣,會簡略報告。為了教學示範與展現負責任的研究態度,請讀者參考以下報告寫作範例:
順時針捲動的平均評分比逆時針捲動的平均評分高0.072分(順時針:M = 0.641, SD = 0.496;無關聯:M = 0.713, SD = 0.473, 95% CI [-0.118 0.263]),並未達到事先宣告的統計顯著水準,t(100) = 0.754, p = .453, d = 0.149。
如果沒有違反變異等量假設與常態分佈假設的問題,在報告裡沒有必要呈現Welch氏t檢定。然而 Delacre, Lakens, and Leys (2017) 建議使用獨立t檢定分析的資料,應該全面採用Welch氏t檢定。有關此建議,請讀者自行尋找論文閱讀及判斷。
7.3 獨立組設計與統計考驗力
Wagenmakers等人的再現研究雖然沒有發現顯著結果,但是給我們一個機會探討效果量較小的研究,要如何改進,才能確保能發現顯著差異,又有起碼80%的考驗力。再度開啟考驗力分析的jamovi示範檔案,最後的jPower報表Independent Samples T-Test顯示如果效果量只有0.15的兩組獨立樣本研究,要得p值通過.05判斷水準,且有80%考驗力的顯著結果,Kitchen Roll的兩群參與者人數需要各有至少699人,總共1398人。以圖7.14的曲線推測,除非這項實驗可測得的效果量能增加,或者降低其望達到的考驗力水準,才能減少參與者的人數。但是降低考驗力水準是本書建議讀者不該採取的策略,即使能得到通過.05判斷水準的p值,實驗結果也不容易再次重現。
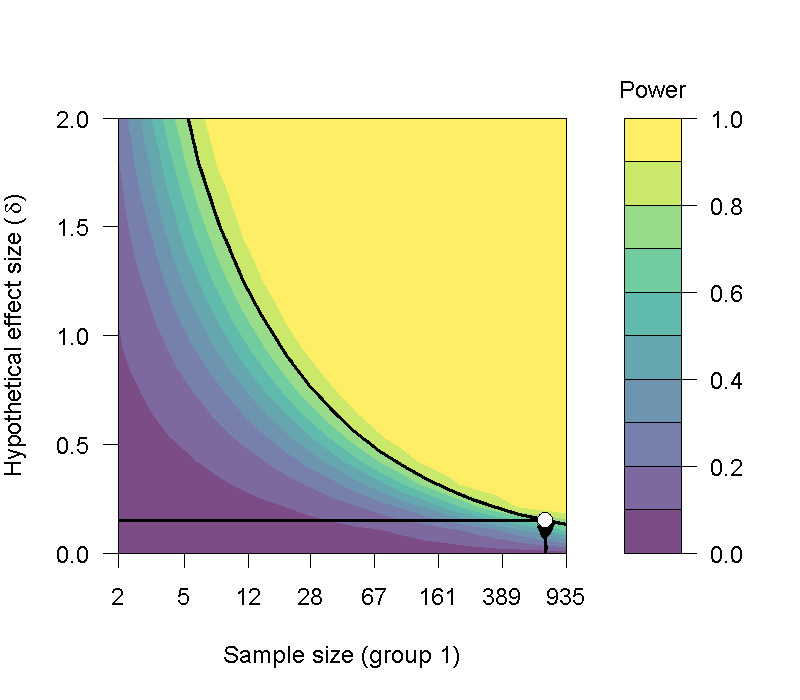
圖 7.14: 達到指定考驗力之獨立樣本t檢定效果量,所需要的樣本數分析。
如果Kitchen Roll可以改成重覆量數設計,收集相依樣本的資料。結果依然測得效果量是0.15,同樣採用雙尾檢定與.05判斷水準進行相依樣本t檢定,jPower的估計顯示需要351人,就能確保顯著結果有80%的考驗力,如圖7.15所示。讀者可透過作業問題的引導,比較兩種設計的考驗力分析,了解為何較難再現的心理科學研究,多數是獨立組設計的研究領域。
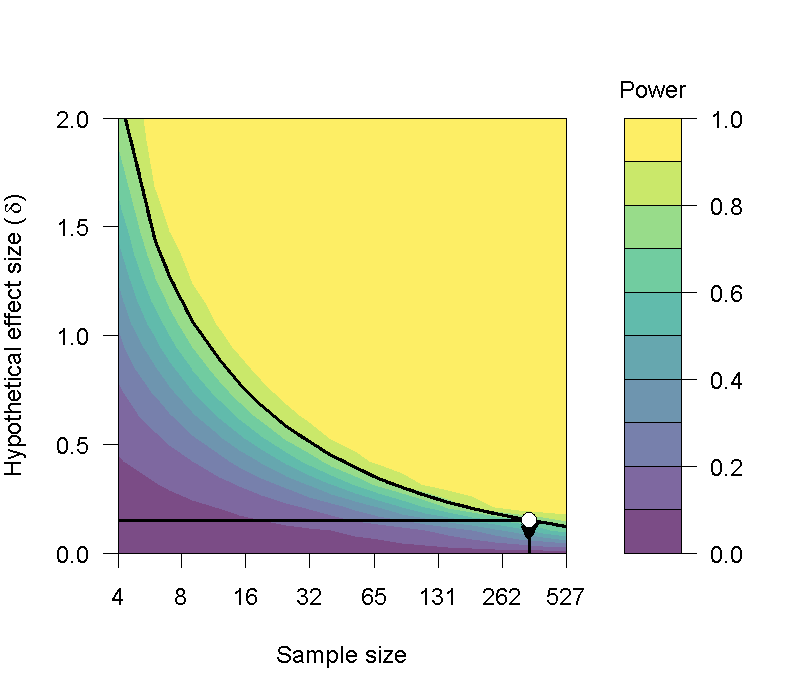
圖 7.15: 達到指定考驗力之相依樣本t檢定效果量,所需要的樣本數分析。
7.4 總結
- TBA
7.5 習題
- TBA
References
Delacre, Marie, Daniël Lakens, and Christophe Leys. 2017. “Why Psychologists Should by Default Use Welch’s T-Test Instead of Student’s T-Test.” International Review of Social Psychology 30 (1): 92–101. https://doi.org/10.5334/irsp.82.
Seo, Dong-Chul, Eric Nehl, Jon Agley, and Shang-Min Ma. 2007. “Relations Between Physical Activity and Behavioral and Perceptual Correlates Among Midwestern College Students.” Journal of American College Health 56 (2): 187–97. https://doi.org/10.3200/JACH.56.2.187-198.
Topolinski, Sascha, and Peggy Sparenberg. 2012. “Turning the Hands of Time: Clockwise Movements Increase Preference for Novelty.” Social Psychological and Personality Science 3 (3): 308–14. https://doi.org/10.1177/1948550611419266.
Wagenmakers, Eric-Jan, Titia F. Beek, Mark Rotteveel, Alex Gierholz, Dora Matzke, Helen Steingroever, Alexander Ly, et al. 2015. “Turning the Hands of Time Again: A Purely Confirmatory Replication Study and a Bayesian Analysis.” Frontiers in Psychology 6 (April). https://doi.org/10.3389/fpsyg.2015.00494.