第1單元 統計思考開門
科學創見從對現象的推測開始,只要好奇親眼目睹或耳聞的現象之發生原因,推測如何發生的過程,就有最初步的假設(Hypothesis)。假設要成為讓人信服的說法,需要有正面證據(Positive Evidence)的支持,以及不被反面證據(Negative Evidence)推翻。決定該找到什麼樣的證據,還有收集證據的方法,與假設放在一起就構成科學思考(Scientific thinking)。當證據是需要經過隨機化(Randomization)取得的資料(Data),並且使用機率模型(Probability Model)整理與驗證資料裡的正反面訊息,這種科學思考就是統計思考(Statistical Thinking)。
1.1 統計思考實例:Emily Rosa的專題研究
曾擔任美國神智學會(Theosophical Society in America)會長的Dora Kunz在1970年代起提倡治療性撫慰(therapeutic touch),幫助病患紓解病痛與焦慮。提倡者主張人類身體自然散發能量場(energy field),受過訓練的治療師能不接觸患者身體,感應患者的能量場,並運用自身能量撫慰患部,紓解病患的痛苦。到了今天,包括美國在內,全球大約有80所護理學校列治療性撫慰為正式課程,光是北美地區有80所左右的醫療機構允許護理人員使用治療性撫慰幫助住院患者。有興趣的讀者使用關鍵詞“therapeutic touch”搜尋網路資訊,還能發現有組織定期舉辦教育工作坊。

圖 1.1: 正在接受治療性撫慰的男士。圖像取自HEAVYSTONES.com
1998年當時11歲的美國女孩Emily Rosa,想知道治療師感應人體能量場的真實能力,改造流傳已久的擲硬幣遊戲,設計出一套簡易測試。她請治療師坐在同一張桌子對面,兩人之間有一塊隔板,雖然能對話但是看不見彼此,隔板下方有兩個孔洞。測試時治療師將雙手穿過孔洞伸到另一邊,每次測試前測試者先投擲硬幣,決定要將自已的手伸到治療師的那一隻手掌上方8至10公分處,再請治療師說出測試者的手是在左手還是右手上方,每位治療師反覆進行十次測試。以擲硬幣對賭的所有可能性來看,Emily假設如果治療師真的有感應人體能量場的能力,十次測試的答對率應該比完全亂猜(50%)高出許多,當年的Emily認為一位治療師至少要答對8次,才能證實真有本事。
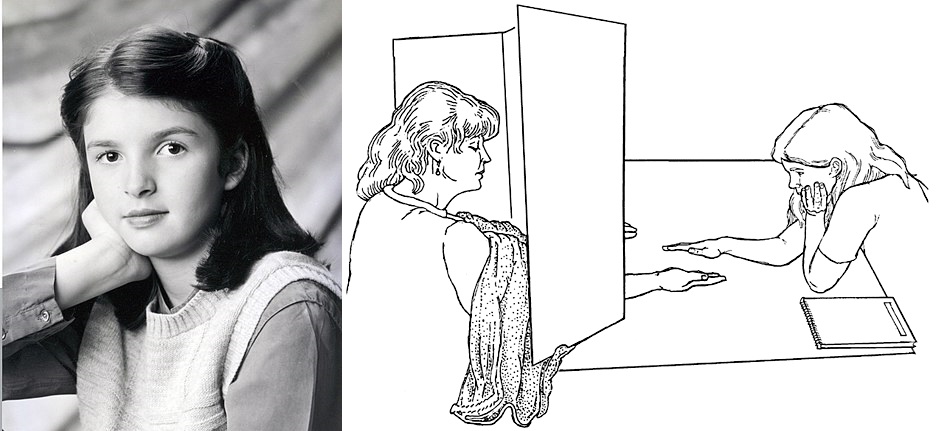
圖 1.2: 左:Emily Rosa 11歲時的留影,取自維基百科。右:Emily Rosa施測現場素描,取自Rosa et al. (1998) Figure 1
在父母的幫助下,1996年Emily邀請到15位實際從事治療性撫慰的人士參與測試,一年後因為電視台的專訪,又找了曾參與先前研究在內的7位等共13位人士,進行第二次研究。Emily與父母以及一位醫師一起將兩次研究結果寫成論文發表(Rosa et al. 1998)。論文中的長條圖呈現28人次的正確次數,圖1.3是原始統計圖的重製版本:
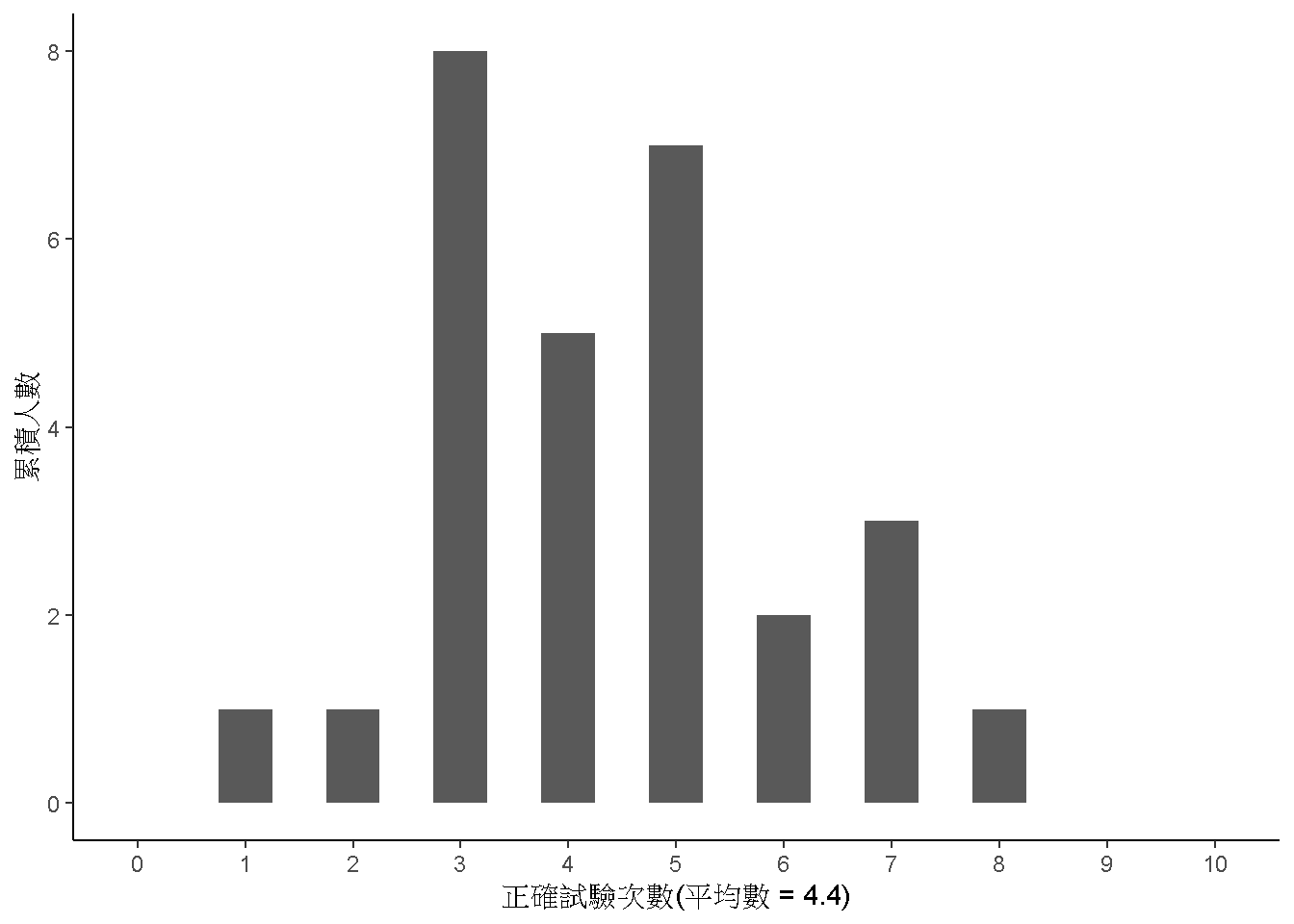
圖 1.3: Emily Rosa的研究結果
測試結果究竟證實了治療師們真有本事?還是揭露治療性撫慰的誇大不實?回答這些問題之前,我們先來解析這件專題研究的思路。如果你認為Emily Rosa的假設與測試方法是有道理的,或者你認為可以做更好的改良,那麼你已經有科學思考的基本能力。Emily的專題研究讓我們知道,能以科學思考探究的問題,必定有可測試的假設,以及可實作的測試方法。更嚴謹的話,還要加上正反證據的成立條件。
那麼為何Emily Rosa的專題研究是一種統計思考?首先Emily提出的假設有預期測量結果的發生機率:如果治療師們沒有宣稱的本事,全部的答對率應該和丟硬幣猜是正面還是反面向上的機率一樣:50%。如果治療師們真的有本事,答對率應該明顯高於50%,這也是正面證據與反面證據有效的條件。至於Emily使用的測試方法,看上去可以有效累積每位治療師的答對率。
圖 1.3 標示21位治療師的平均答對次數是4.4次,表示10次測試裡有4至5次是正確的。平均4.4次似乎與50%差不了多少,憑這個數值,Emily能推斷這群治療師的本事言過其實嗎?
1.2 統計思考養成途徑
Emily Rosa的報告裡是以數值呈現的機率資訊,判斷治療師有本事的可能性,有沒有高過治療師沒有本事的可能性。她所收集的資料,能以全部治療師的正確反應次數估計可能性,也可以每位治療師的正確率估計可能性。本書運用這個案例,介紹每位統計初學者首先學習的單一樣本樣本推論統計(第5單元)。
學習第一套推論統計之前,我們要先認識描述資料的方法,也就是描述統計。描述統計的功用是劃清要進行推論的資訊,符合想確證的假設。好的描述統計能展現分析者對問題的理解,以及從資料獲得的判斷。在第2單元,我們將學習類別變數與連續變數的資料尺度以及統計量數,還有表現各種變項組合的統計圖表。
接著在第3單元,我們要重新學習機率事件的計算,以及機率分佈的概念,再次深入了解何謂條件機率,以及運用貝氏定理計算事後機率。到了第4單元,我們要運用程式模擬認識機率分配,探討為何在隨機化條件下收集的資料,才是能代表母群的樣本。這兩個單元都會運用相同的案例,介紹機率的計算與模擬。
充分認識機率的計算與模擬,我們就能運用這些觀念與方法,理解推論統計的運作邏輯。第5單元以TT治療師的測試分析,學習假設檢定的正確運用方法,我們將了解如何考量無窮次的型一與型二錯誤率,謹慎推論一次的顯著性檢定結果;還有初步認識母數推論統計與無母數推論統計的差異。
第6單元將前進到相依樣本的推論統計,在此將認識第一種效果量:標準化平均數差異,以及如何搭配樣本數及考驗力等資訊,判斷推論結果的可靠性。第7單元以獨立樣本的推論統計範例,讓初學者認識實驗設計如何影響分析結果。
第8單元將認識第二種效果量:相關係數,以及最簡單的一元一次線性迴歸式。這個單元的範例與第6單元與第7單元有所關聯,以此引導初學者了解兩種推論方法與變異數分析的關聯性。進入第9單元,就能運用線性迴歸了解正確使用變異數分析的關鍵,以及解讀及呈現分析結果的方式。
1.3 統計方法運用指南
本書編排架構參考Rivka de Vries博士建置的教學網站統計貓咪(statkat),以分析問題的變項結構設定篇章介紹統計方法。鑑於本書預設讀者是尚未有豐富統計分析實務的初學者,集中介紹適用單一自變項與單一應變項之間,或者只有一個獨變項與一個依變項的統計方法。我將本書介紹的方法,與章節連結整理於下表:
| 依變項為類別變項 | 依變項為連續變項 | |
|---|---|---|
| 無獨變項 | 二項檢定( 單元5.3 ) | 單一平均數z檢定( 單元?? ) |
| 獨變項為相依樣本 | McNemar氏檢定( 單元6.1 ) | 相依樣本t檢定(單元6.2) |
| 獨變項為獨立樣本 | 卡方獨立性檢定(單元7.1) | 獨立樣本t檢定(單元7.2) |
| 單一自變項為連續變數 | 皮爾森相關(單元8.2), 簡單迴歸(單元8.3) | |
| 單一獨變項有三組以上獨立樣本 | 獨立樣本變異數分析(單元9.1) | |
| 單一獨變項有三組以上相依樣本 | 重覆量數變異數分析(單元??) |
讀者除了可由表格快速找到自已想查閱的章節資料,這份表格也是統計貓咪(statkat)提供的方法檢索表微型版。當讀者熟練本書介紹的統計方法之後,一旦有需要學習其他統計方法,可經由該網站尋找相關資訊。該如何找到自己需要的統計方法?就要從了解變項的性質開始,所以下一章要好好認識描述統計。
1.4 總結
- 科學思考講究平等對待正面證據與反面證據;統計思考透過機率模型評估各種證據的可能性。
- 養成統計思考需要洞察肯定或否定理論的證據皆可能發生,也需要不斷自我提醒,當下得到的結果只是長久觀察的一種可能性。
- 任何需要統計分析的資料必有依變項,分析之前先確認測量尺度,能掌握合適的分析方法。
1.5 習題
安裝與設定JASP與jamovi。如果電腦有連接網路,由jamovi的模組選單(Modules),下載試用
Rj、statkat、以及learning statistics with jamovi。根據你的學習指南,開啟指定的JASP與jamovi資料收藏檔案,進行第一次嘗試並儲存分析結果。
註冊OSF與管理管理專案,上傳展示你的第一次分析結果。
References
Rosa, Linda, Emily Rosa, Larry Sarner, and Stephen Barrett. 1998. “A Close Look at Therapeutic Touch.” JAMA 279 (13): 1005. https://doi.org/10.1001/jama.279.13.1005.