《用jamovi上手統計學》導讀

假設檢定 9-1~9-4

人類有透視能力嗎？

Bem, D. J. (2011). Feeling the future: Experimental evidence for anomalous retroactive influences on cognition and affect. Journal of Personality and Social Psychology, 100(3), 407–425. https://doi.org/10.1037/a0021524

generated by ChatGPT4.

假設的層次

  • 能讓人根據說法，構想研究情境的主張
    • 只要經過開發，人人都能有透視能力。
    • 人人都有透視能力。
    • 運用隨機方法設定的雙盲測試，人人有透視能力的話，猜對機率會多於隨機。
    • 運用隨機方法設定的雙盲測試，人人有透視能力的話，猜對的人數與多於猜錯的人數。

以數學符號構成的模型，指示樣本資料生成機制(母群)的條件。

研究假設的主張 統計假設模型的條件
沒有透視能力 \(\theta=0.5\)
有透視能力且能辦試顏色 \(\theta > 0.5\)
有透視能力但辦試顏色失誤 \(\theta < 0.5\)
有透視能力但不確定辨色能力 \(\theta \neq 0.5\)
  • 此處的\(\theta\)指二項分佈的成功機率
  • \(\theta\) 也是泛用母群參數

統計假設模型的設定

  • 虛無假設(\(H_0\))
    • 與研究假設主張相反的統計條件
  • 對立假設(\(H_1\))
    • 與研究假設主張一致的統計條件
  • 研究者主張”人人都有透視能力”
    • \(H_0\): \(\theta = 0.5\)
    • \(H_1\): \(\theta \neq 0.5\)

假設檢定的決策失誤

運用推論統計做決策：以研究樣本資料所總結的母群參數估計值，是適配虛無假設的條件，還是對立假設的條件。

保留\(H_0\) 拒絕\(H_0\)
\(H_0\)為真 正確決策 型一決策錯誤
\(H_0\)為假 型二決策錯誤 正確決策

型一(決策)錯誤率 \(\alpha\)

型二(決策)錯誤率 \(\beta\)

保留\(H_0\) 拒絕\(H_0\)
\(H_0\)為真 1 - \(\alpha\) \(\alpha\)
\(H_0\)為假 \(\beta\) 1 - \(\beta\)

取樣分佈與統計推論

透視能力測試樣本資料符合二項分佈: \(P(X|\hat{\theta},N)\)

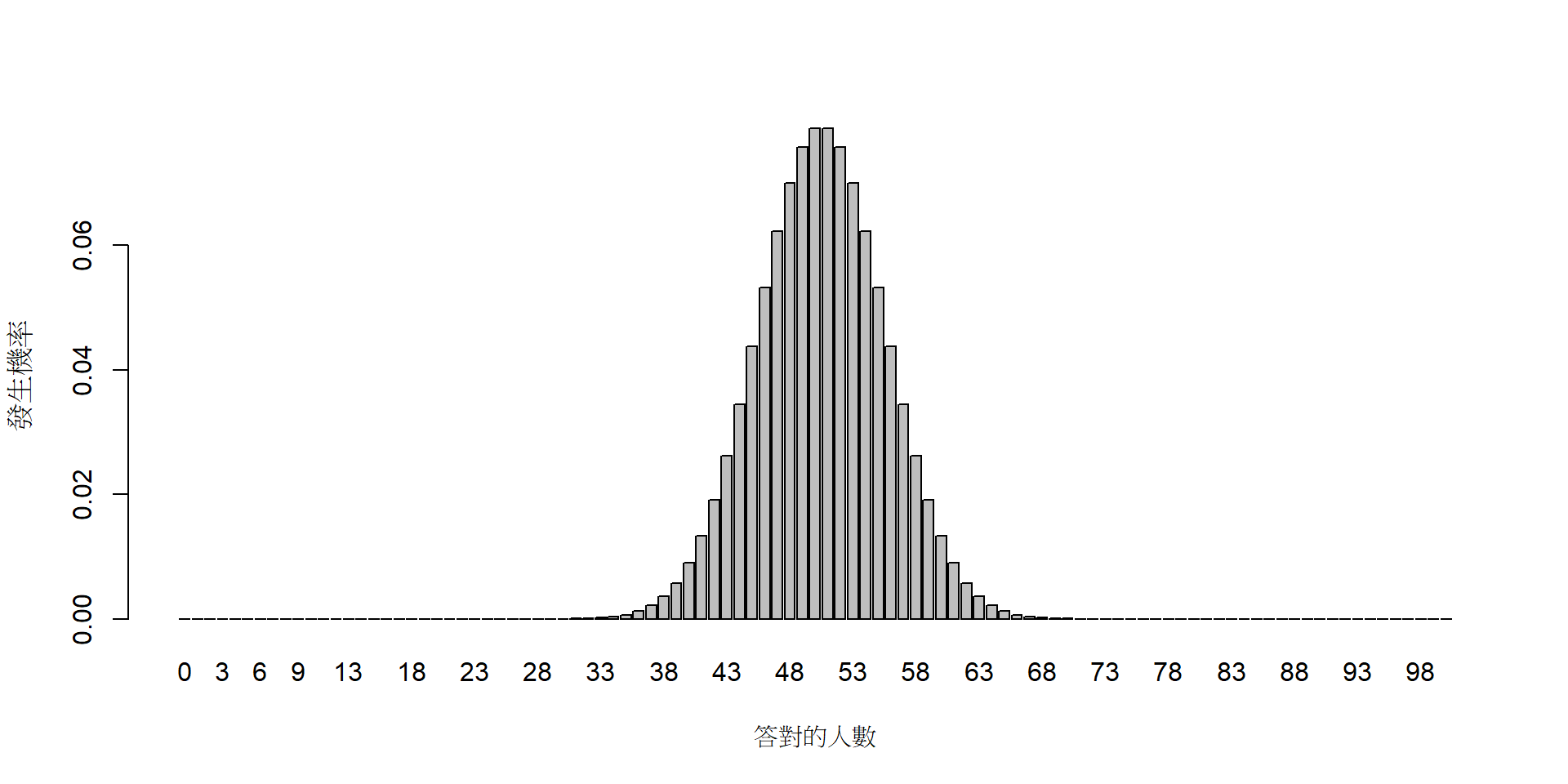
符合虛無假設的(理論)取樣分佈

  • \(H_0\): \(P(X|\hat{\theta} = 0.5, N = 100)\)
  • \(H_1\): \(P(X|\hat{\theta} \neq 0.5, N = 100)\)

統計推論的棄卻域與臨界值

  • 最近一次的100人測試結果有62人答對 \(X = 62\)
  • 要判斷\(X = 62\)有多大的機率來自 \(H_0\): \(P(X|\hat{\theta} = 0.5, N = 100)\)
  • 依顯預期的型一錯誤率 \(\alpha\)設定顯著水準
  • 根據顯著水準，在虛無假設的取樣分佈畫定棄卻域
  • 臨界值就是棄卻域的邊界
  • jamovi distACTION示範

單側與雙側檢定

\(H_0\): \(\theta = 0.5\) or \(P(X|\hat{\theta} = 0.5, N = 100)\)

\(H_1\): \(\theta \neq 0.5\) or \(P(X|\hat{\theta} \neq 0.5, N = 100)\)

  • 棄卻域分隔於取樣分佈的兩側
  • 臨界值有兩條
  • 只適用取樣分佈符合二項分佈、常態分佈、t分佈…

\(H_0\): \(\theta \le 0.5\) or \(P(X|\hat{\theta} \le 0.5, N = 100)\)

\(H_1\): \(\theta > 0.5\) or \(P(X|\hat{\theta} > 0.5, N = 100)\)

  • 棄卻域只在取樣分佈一側
  • 臨界值有一條
  • 適用任何性質的取樣分佈

統計顯著的真實意義

  • “significant”的語意變遷
  • 統計顯著代表研究假設的主張獲得支持？