《用jamovi上手統計學》導讀

比較單一與兩組平均值 11-2 ~ 11-9

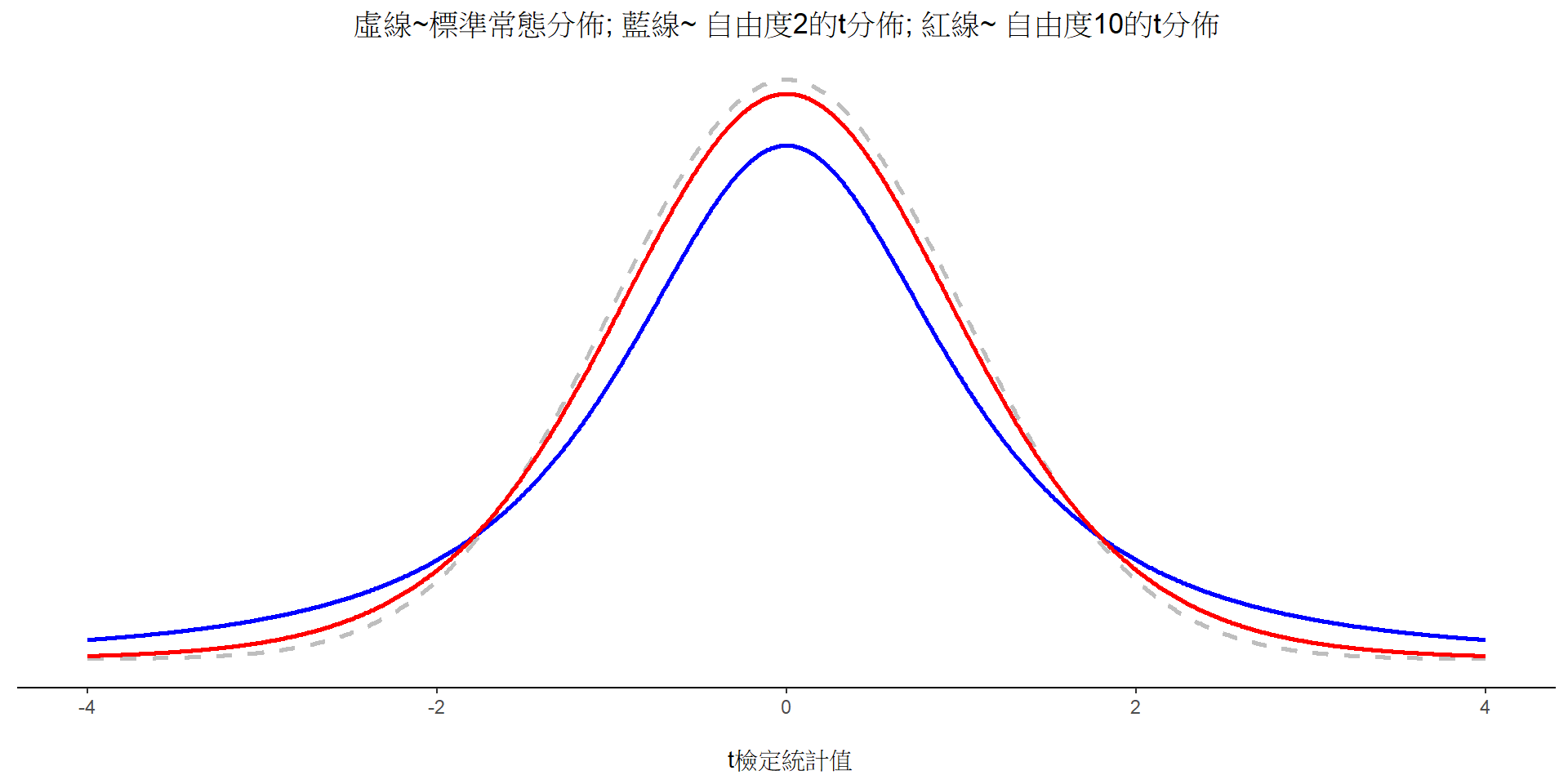
t檢定的使用時機及適用條件

  • 比較單一分組或兩組之間的平均值。
  • 無法估計母群變異數。
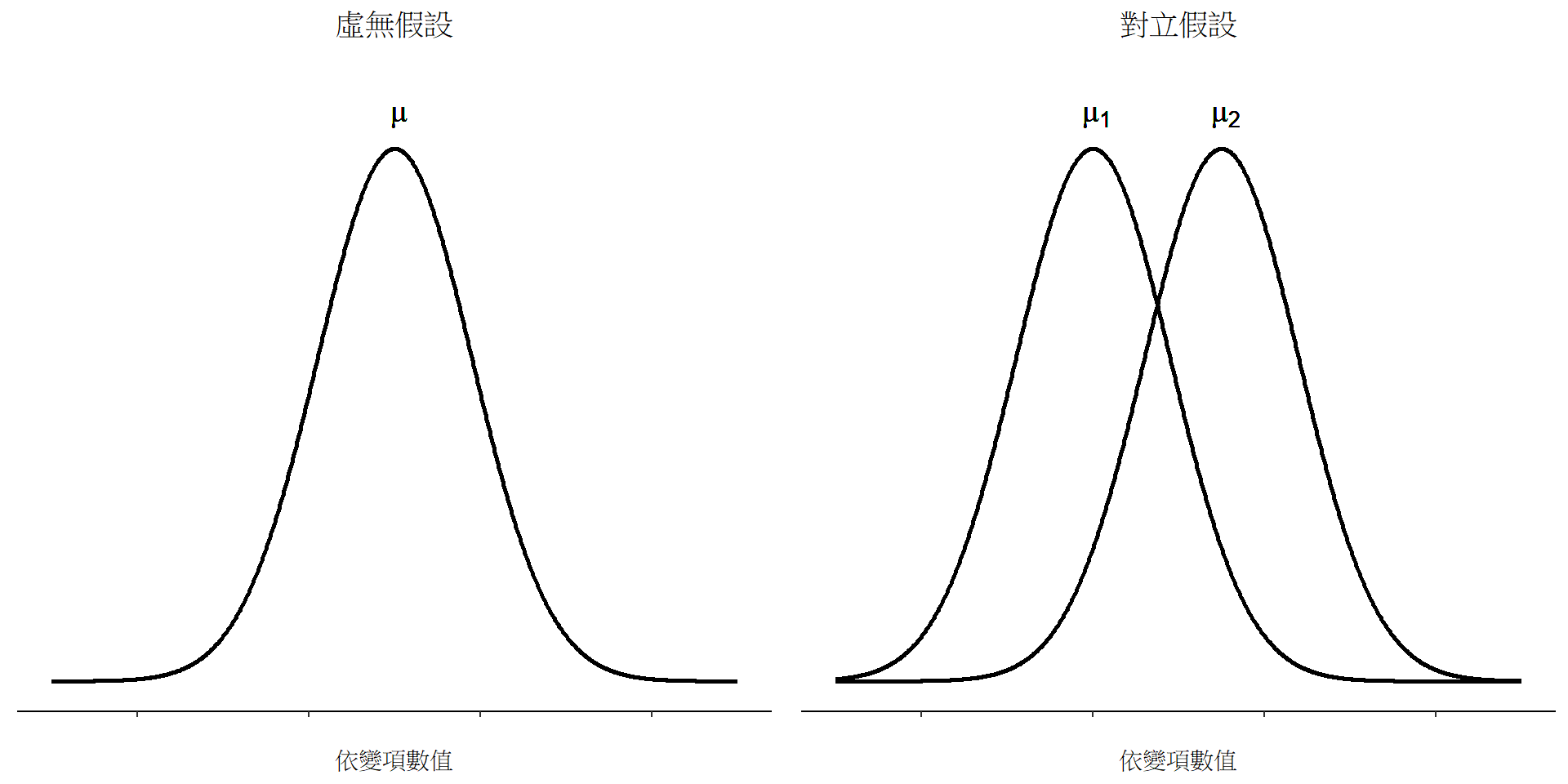
  • 單一分組樣本平均值\(\bar{Y}\)是否相等於母群平均值之估計值\(\hat{\mu}\)？
  • 兩個分組的樣本平均值\(\bar{X_1}\)與\(\bar{X_2}\)各自估計的母群平均值彼此相等\(\hat{\mu_1}\) = \(\hat{\mu_2}\)？
  • 相依樣本的差異分數平均值\(\bar{X_D}\)是否相等於差異分數的母群平均值\(\hat{\mu}_D\)？
  • 除了參數設定，t分佈與常態分佈的性質一樣
  • jamovi distrACTION示範
  • 樣本平均值的取樣分佈符合常態分佈。
  • 構成樣本平均值的樣本數值來源彼此無任何關聯。
  • 以上條件都不適用時，應採用對應的無母數方法。

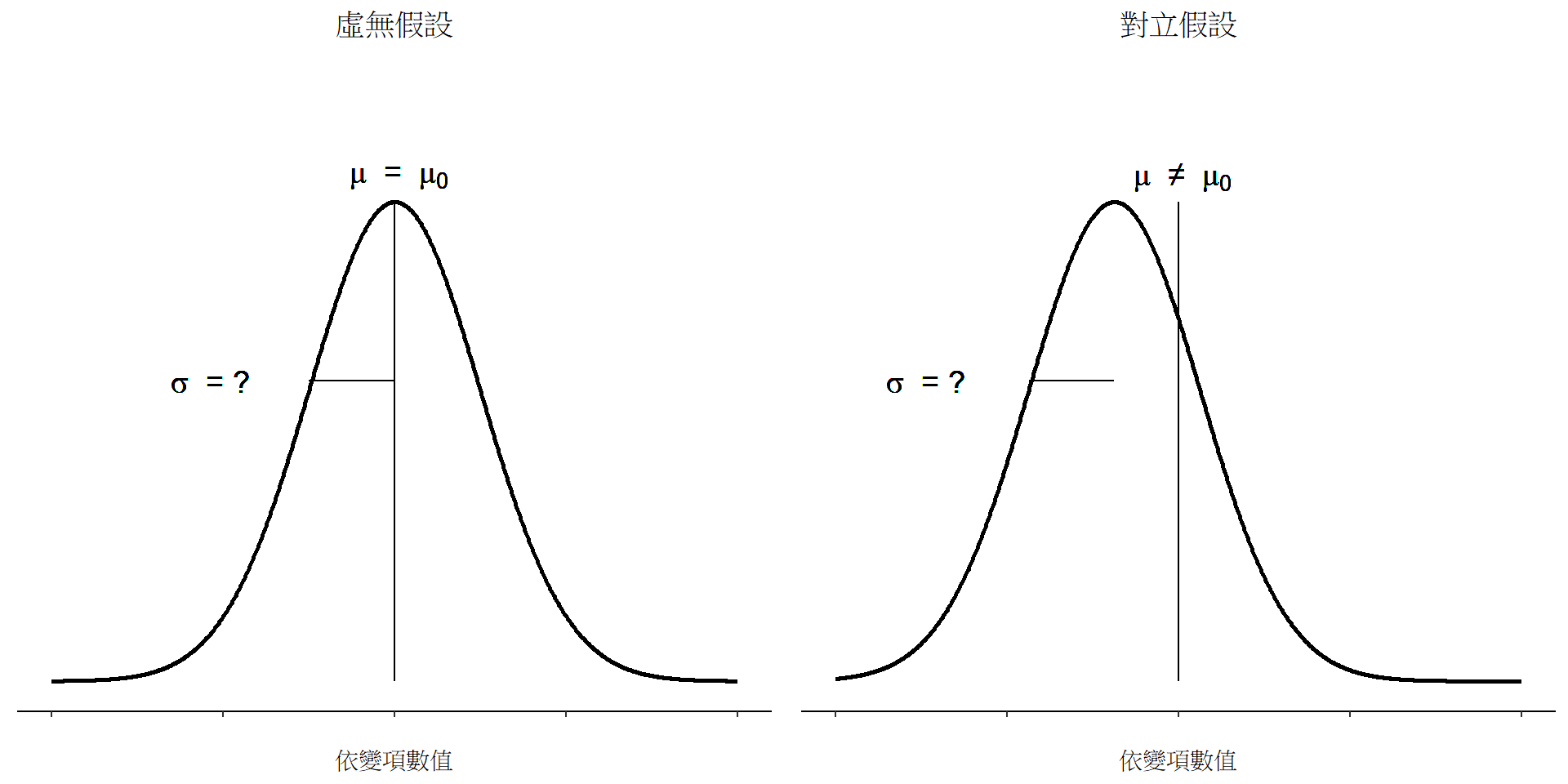
單一樣本t檢定

只有單一分組樣本資料平均值\(\bar{Y}\)及樣本標準差\(s = \sqrt\frac{\sum(Y-\bar{Y})^2 }{n-1}\)

jamovi distrACTION示範

\(t=\frac{\bar{Y}-\mu}{\frac{\hat{\sigma}}{\sqrt{N}}}=\frac{\bar{Y}-\mu}{\frac{s_{\bar{Y}}}{\sqrt{N}}}\)

獨立樣本t檢定

只有兩群分組樣本資料平均值\(\bar{Y}_1\)與\(\bar{Y}_2\)，及分組樣本標準差\(s_1\)及\(s_2\)。分組樣本量\(n_1\)與\(n_2\)不一定相等。

分組樣本標準差相等 分組樣本標準差不相等
t統計值 \(t=\frac{\bar{X}_1-\bar{X}_2}{SE(\bar{X}_1-\bar{X}_2)}\) \(t=\frac{\bar{X}_1-\bar{X}_2}{SE(\bar{X}_1-\bar{X}_2)}\)
估計標準誤(SE) \(\hat{\sigma}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}\) \(\sqrt{\frac{\hat{\sigma}_1^2}{n_1}+\frac{\hat{\sigma}_2^2}{n_2}}\)
df \(n_1 + n_2 -2\) \(\frac{\left( \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} \right)^2 } { \quad \frac{s_1^4}{n_1^2 \nu_1} + \frac{s_2^4}{n_2^2 \nu_2 } \quad }\)

\(\nu_i \sim 各組樣本資料自由度\)

即使分組樣本量不一樣…

  • 變異數同質性檢核顯示兩組樣本標準差沒有顯著差異：Student’s t test
  • 變異數同質性檢核顯示兩組樣本標準差有顯著差異：Welch’s t test

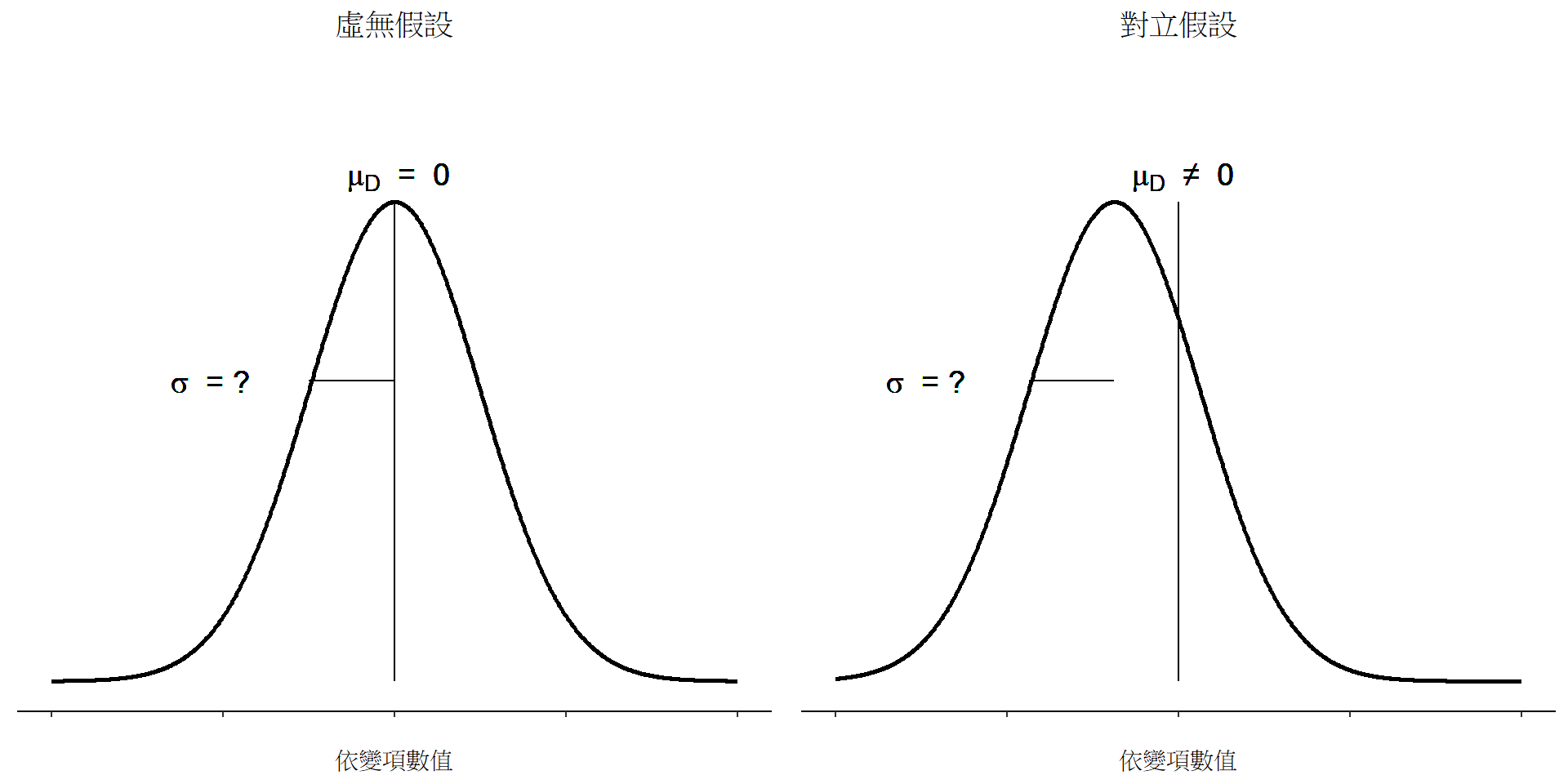
相依樣本t檢定

同一位參與者前後測試的差異分數(D)，或參與重覆量數設計於不同條件測得的表現差異分數(D)所構成的樣本資料平均值\(\bar{D}\)及樣本標準差\(s = \sqrt\frac{\sum(D-\bar{D})^2 }{n-1}\)

請見單一樣本t檢定

樣本資料的相關性 差異分數方向一致性

t檢定的效果量

  • 務必要勾選”Effect Size”
  • 可比較相同設計、不同研究的結果差異。

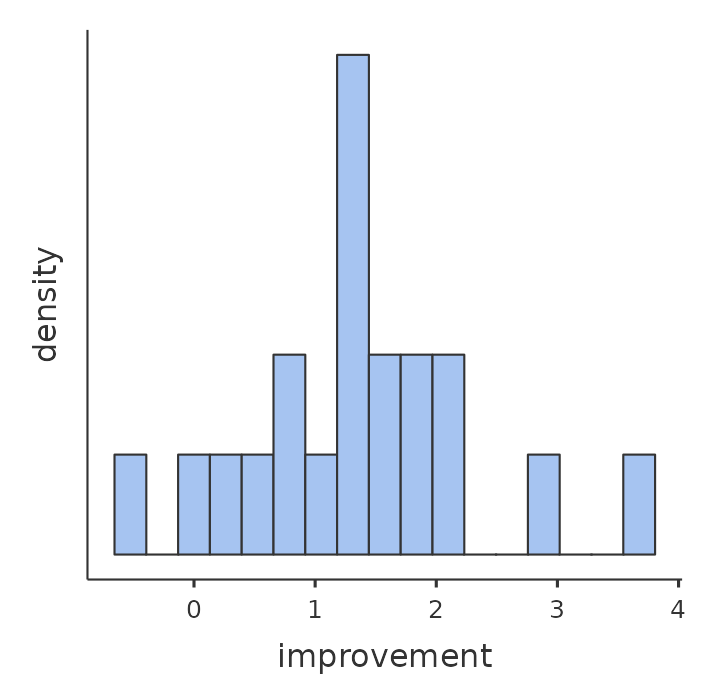
檢核t檢定的常態性

  • Q-Q 圖
  • Shapiro-Wilk檢定
  • 統計圖與檢定並用
  • 圖11.25的例子